9/12/2010 1
CHÖÔNG 4
NGAÉN MAÏCH TRONG HEÄ THOÁNG ÑIEÄN
Baøi 4-1Khaùi nieäm chung
Baøi 4-2 Ñaëc ñieåm doøng ñieän ngaén maïch
Baøi 4-3 Tính toaùn ngaén maïch ñoái xöùng
Baøi 4-4 Söï coá baát ñoái xöùng
Baøi 4-6 Haïn cheá doøng ñieän ngaén maïch trong caùc trang bò ñieän
9/12/2010 2
BÀi 4-1 KHÁI NIỆM CHUNG
1. Định nghĩavàđặctính
Định nghĩa:
Ngắnmạch chỉhiệntượng:
¾Các dây pha chạm nhau
¾Dây pha chạmđất
¾Dây pha chạm dây trung tính (lưới có trung tính nốiđấtt)
9/12/2010 3
BÀi 4-1 KHÁI NIỆM CHUNG
1. Định nghĩavàđặc tính
Đặc tính:
Khi xảyrangắnmạch:
Tổng trởhệthống giảmxuống
Dòng điệntăng lên, điệnápgiảmxuống
Mứcđộ giảmtổng trở, tăng của dòng điện
hay giảmcủađiệnápphụthuộcvàovịtrí
điểmngắnmạch.
9/12/2010 4
BÀi 4-1 KHÁI NIỆM CHUNG
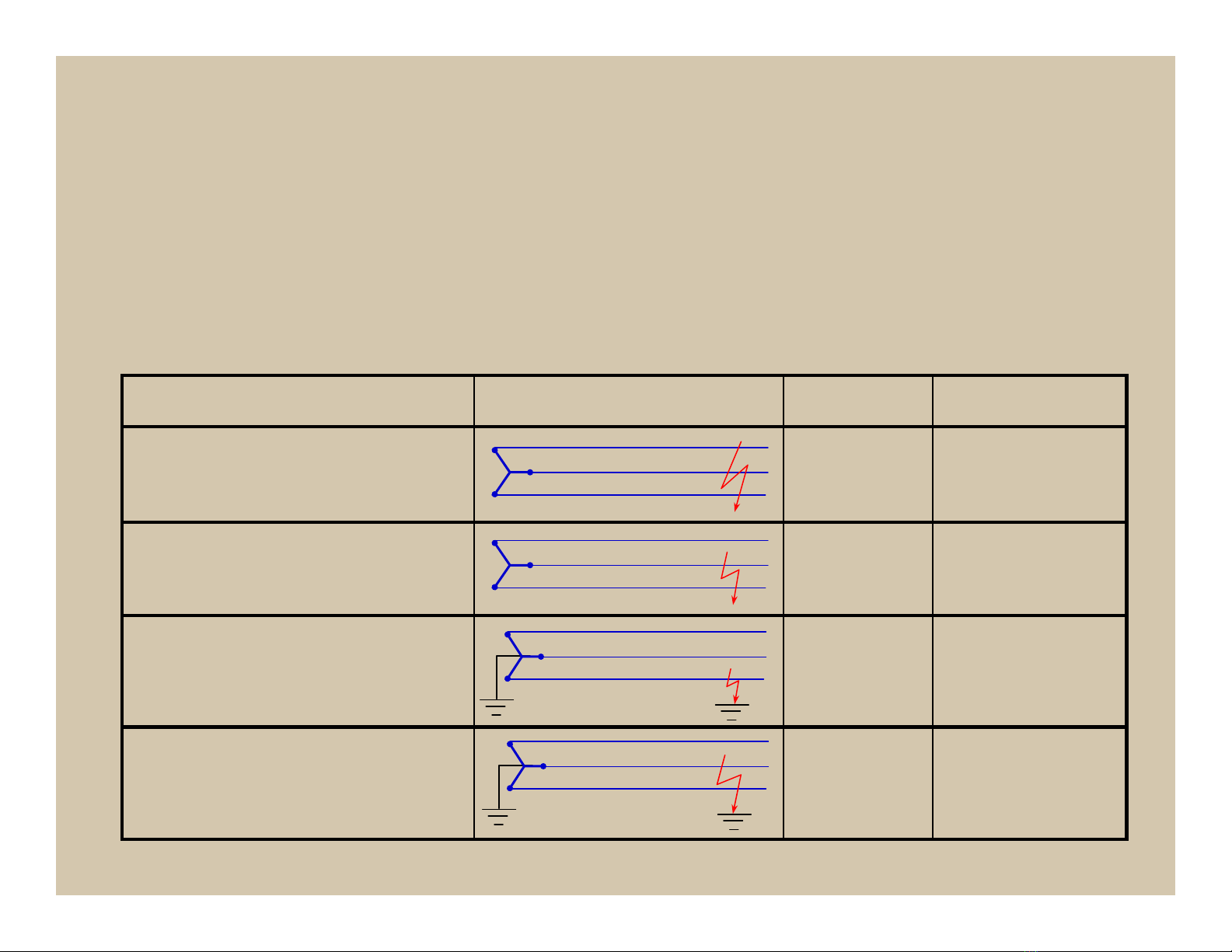
2. Phân loại
a. Ngắnmạch ba pha, N(3)
b. Ngắnmạch hai pha, N(2)
c. Ngắnmạch một pha, N(1)
d. Ngắnmạch hai pha nốiđất, N(1,1)
9/12/2010 5
BÀi 4-1 KHÁI NIỆM CHUNG
2. Phân loại
20N(1,1)
Ngắnmạch hai pha nốiđất
65N(1)
Ngắnmạch một pha
10N(2)
Ngắnmạch hai pha
5N(3)
Ngắnmạch ba pha
X.suất(%)Kí hiệuHình qui ướcLoạiNM