
6262
Chương 4. ĐỘNG LỰC HỌC LƯU CHẤT
1. Phương trình vi phân chuyển động của lưu chất
2. Phương trình năng lượng
3. Tích phân phương trình Euler
4. Phương trình Bernoulli cho dòng chảy của lưu chất thực
5. Phương trình biến thiên động lượng
63
1.
PHƯƠNG TRÌNH VI PHÂN C.ĐỘNG CỦA LƯU CHẤT (1/3)
1.1
Phương trình Euler cho chuyển động của lưu chất lý tưởng (1757).
Lưu chất lý tưởng: =0 =0 sử dụng khái niệm áp suất thủy động tương tự áp suất thủy tĩnh:
x
z
F
y
dx
dy
dz
p,
x
p
p
2
dx
x
p
p
ii
p
z
p
F
dt
du
z
z
1
y
p
F
dt
du
y
y
1
Tương tự:
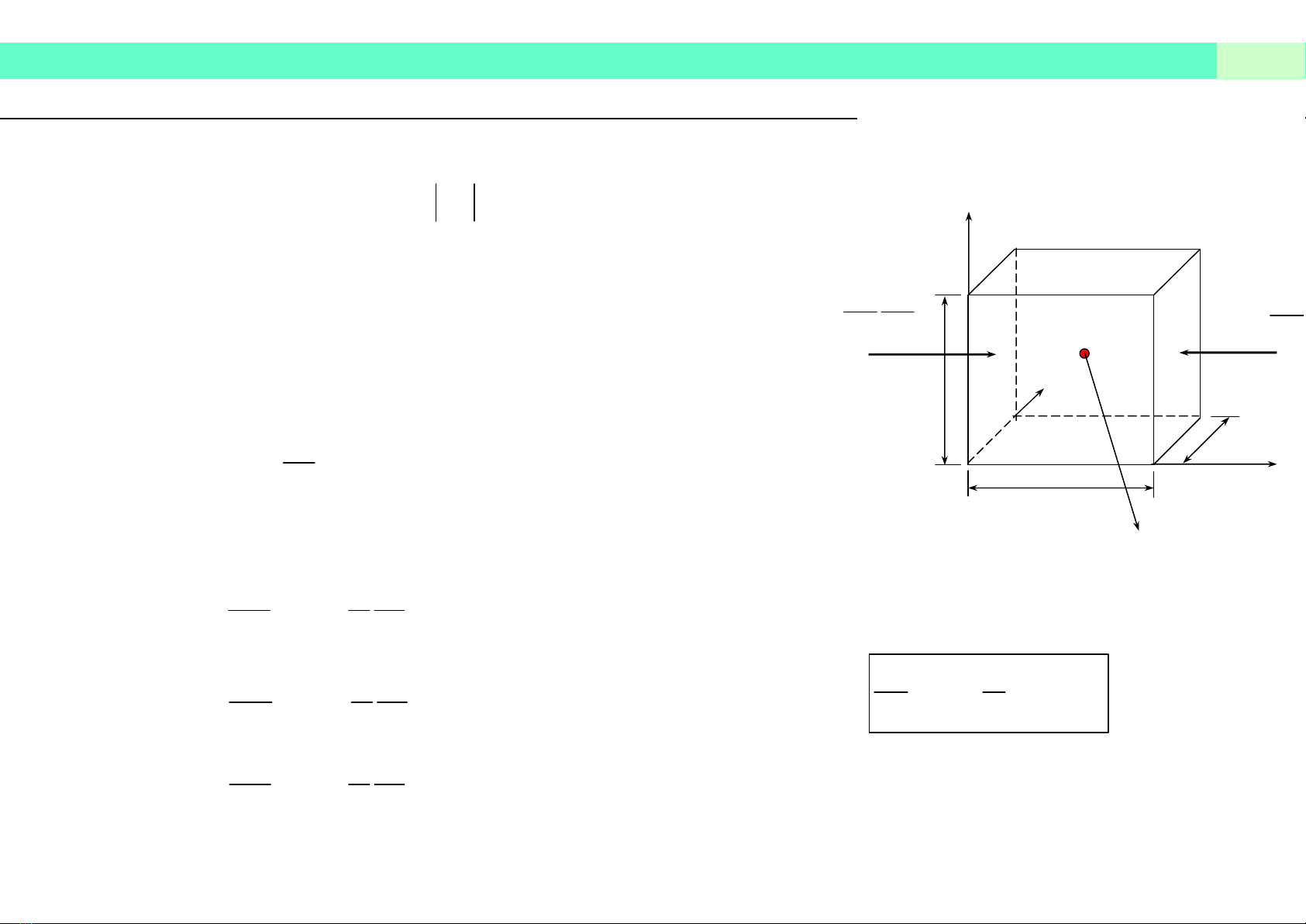
Ngoại lực tác dụng lên phần tử trên
phương x:
• Lực khối:
• Lực mặt:
x
Fdxdydz..
dxdydz
x
p
x
p
F
dt
du
x
x
1
Viết phương trình Định luật II Newton trên phương x cho phần tử =>
pgradF
dt
ud
1
=>
Pgs.Ts
64
1.
PHƯƠNG TRÌNH VI PHÂN C.ĐỘNG CỦA LƯU CHẤT (2/3)
1.2
Phương trình Navier-Stokes cho lưu chất thực (1821-1845).
Lưu chất thực: 0 0
zyx
F
dt
du
zx
yx
xx
x
x
1
Pt định luật II Newton trên phương x => Pt Navier trên phương x
ij
ll
l
i
j
j
i
ijij x
u
x
u
x
u
p
3
2
Giả thiết Stokes (1845):
zzyyxx
p
3
1
Trong
đó p: áp suất thủy động, với:
x
z
F
dx
dy
dz
dz
z
zx
zx
xx
zx
yx
y
yx
yx
xx
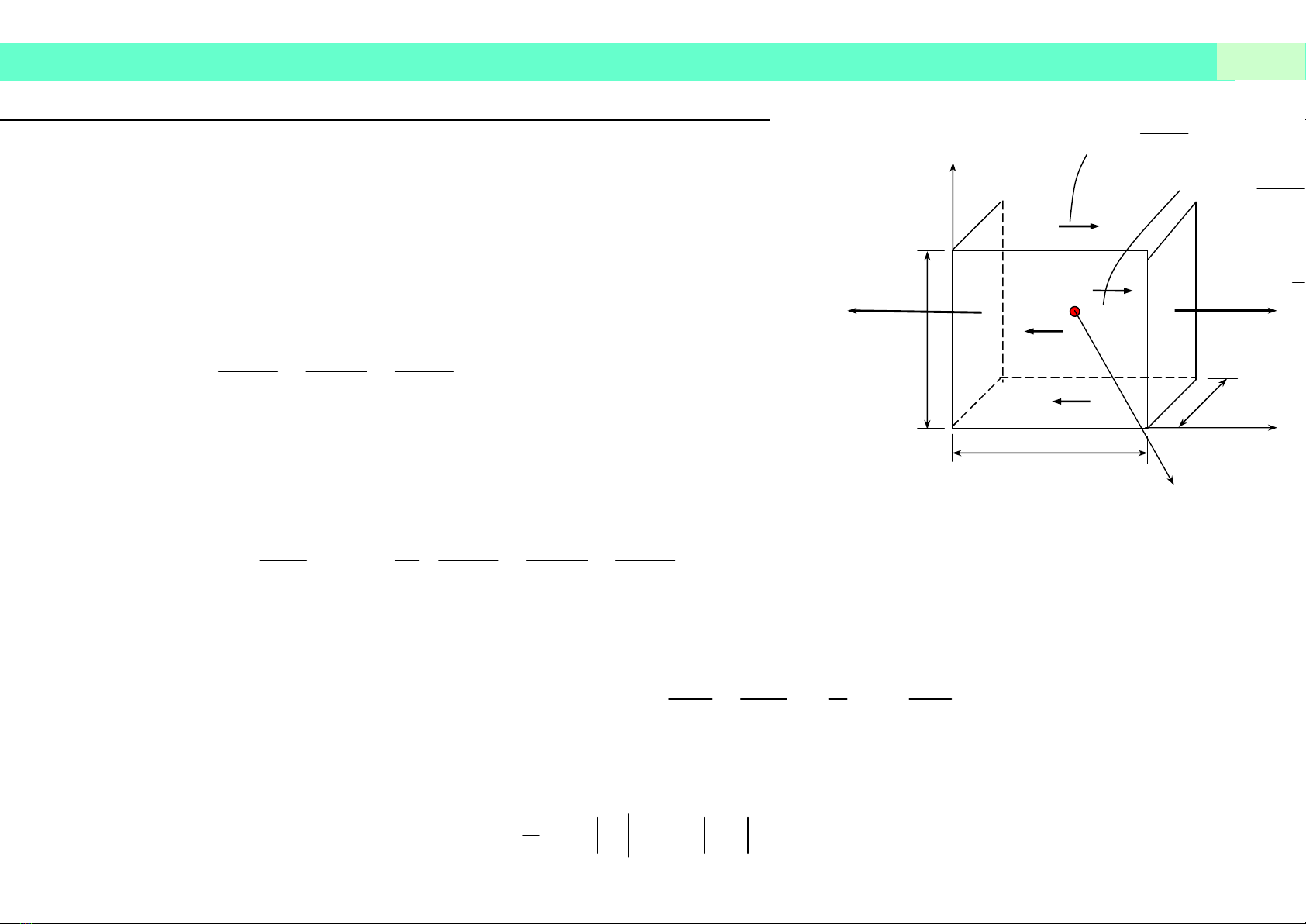
Ngoại lực tác dụng lên phần tử trên phương x:
- Lực khối:
- Lực mặt:
dxdydz
zyx
zx
yx
xx
x
Fdxdydz..
Pgs.Ts

65
1.
PHƯƠNG TRÌNH VI PHÂN C.ĐỘNG CỦA LƯU CHẤT (3/3)
Thay c.thức Stokes vào pt Navier => pt Navier-Stokes.
Trên phương x:
z
u
y
u
x
u
xz
u
y
u
x
u
x
p
F
dt
du z
y
xxxx
x
x
3
11
2
2
2
2
2
2
uupgradF
dt
ud
3
11 2
Pt Navier-Stokes Dưới dạng vector:
upgradF
dt
ud
2
1
Pt Navier-Stokes cho lưu chất không nén được:
uu
t
u
z
u
u
y
u
u
x
u
u
t
u
dt
ud
zyx
Lưu ý gia tốc được tính:
Ẩn số: , p (và cả ρ nếu lưu chất nén được)
u
Pgs.Ts

66
2.
PHƯƠNG TRÌNH NĂNG LƯỢNG (1/3)
2.1
Phương trình vận tải năng lượng:
Định luật bảo toàn năng lượng (ĐL thứ nhất của nhiệt động lực học): Tốc độ biến thiên của năng lượ
ng
phần của một hệ bằng tổng công suất cơ học và công suất của các dòng năng lượng khác mà hệ nhận
đư
S
e
n
S
n
VV
dSqdSudVuFdVe
u
dt
d
..
2
2
e
q
Tce V
cT
e
e: nội năng (chất khí: ; chất lỏng: )
: dòng nhiệt riêng đi vào qua bề mặt bao bọc
.TλTλ.gradq
Định luật truyền nhiệt Fourier:
Vj i
iij
j
Sj
jj
S
n
dVu
x
dSundSu
.
VVS
e
ndVTdVqdSq
.
Biến đổi theo Gauss:
Tu
x
uFe
u
dt
d
j i
iij
j
i
ii
11
2
2
Thay vào pt bảo toàn năng lượng, thu được pt vận tải năng lượng toàn phần:
Pgs.Ts







![Bài giảng Cơ học chất lỏng lý thuyết [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2022/20220516/andromedashun/135x160/7851652705482.jpg)






![Bài tập trắc nghiệm Kỹ thuật nhiệt [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250613/laphong0906/135x160/72191768292573.jpg)
![Bài tập Kỹ thuật nhiệt [Tổng hợp]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250613/laphong0906/135x160/64951768292574.jpg)

![Bài giảng Năng lượng mới và tái tạo cơ sở [Chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2024/20240108/elysale10/135x160/16861767857074.jpg)








