118118118
CHƯƠNG 6
DÒNG CHẢY ĐỀU TRONG KÊNH HỞ
1. Các khái niệm.
2. Tính toán dòng chảy đều trong kênh hở.
3. Mặt cắt lợi nhất về mặt thủy lực
4. Xác định hệ số nhám.
119
1. C
ÁC KHÁI NIỆM (1/1)
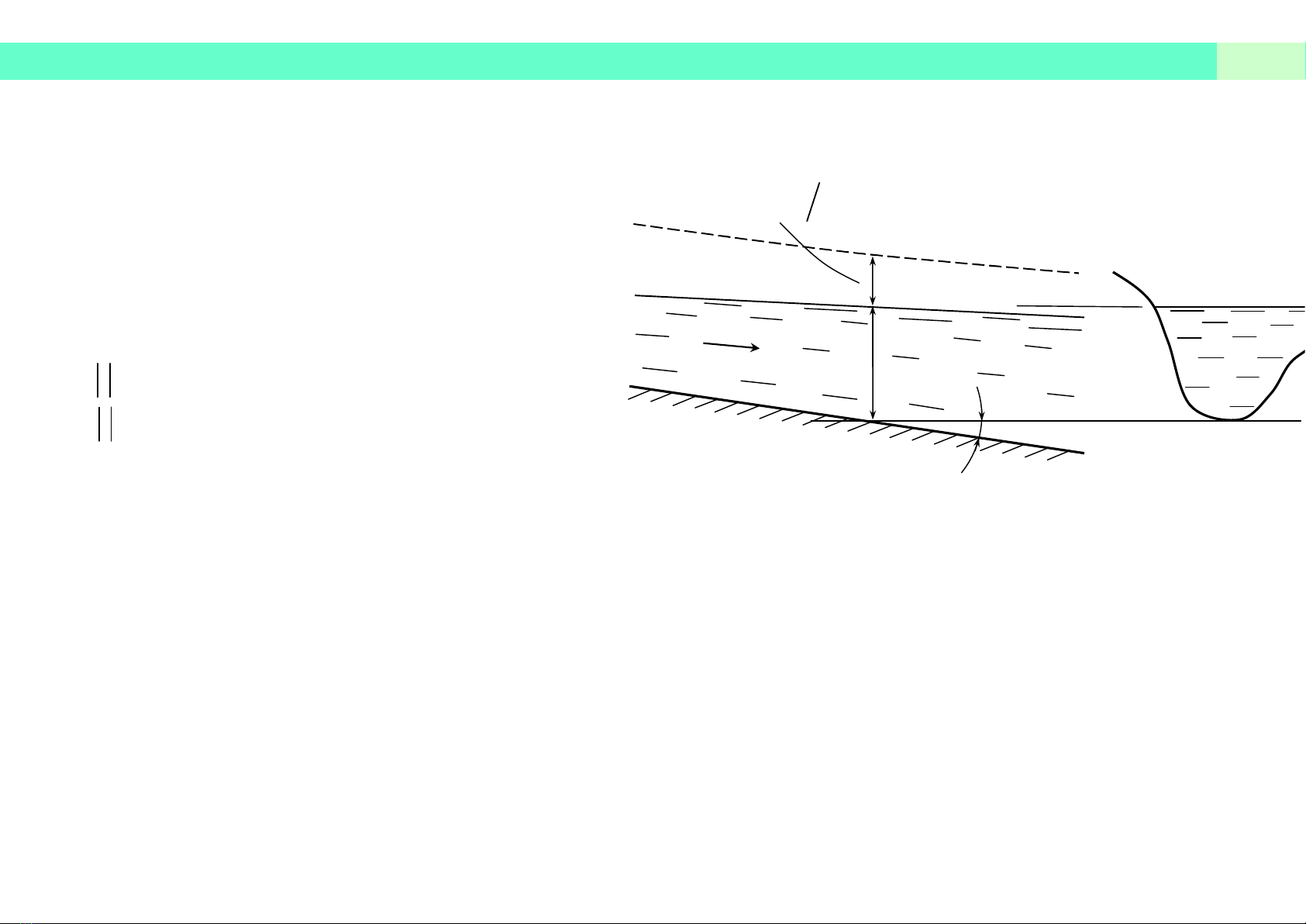
Dòng chảy trong kênh hở: là dòng chảy 1 chiều có mặt thoáng (áp suất trên mặt thoáng có thể bằ
ng
khác áp suất không khí trời)
h
i
P
P
E
E
Q
gV 2
2
Dòng chảy đều: là dòng chảy mà các đặc trưng của nó (vận tốc, độ sâu, diện tích mặt cắt ngang…)
không
đổi dọc theo dòng chảy.
Dòng chảy đều chỉ xảy ra trong kênh lăng trụ có i > 0
Các thông số:
• h – Độ sâu
• i – Độ dốc đáy (i=sin)
1 i
1O i
Phân biệt:
- kênh
- dốc nước
Độ dốc nhỏ => xấp xỉ:
• Đường đo áp P-P trùng với mặt thoáng
• Mặt cắt ướt tính toán = mặt cắt ngang thẳng đứng
Trạng thái chảy:
• Chảy tầng (ReR< 560)
• Chảy rối
Pgs.Ts
120
2. T
ÍNH TOÁN DÒNG TOÁN ĐỀU TRONG KÊNH HỞ (1/7)
2.1
Công thức Chezy
Tính toán dòng chảy trong kênh, người ta thường dùng công thức Chezy:
Hay
Các thông số:
• A, R – Diện tích mặt cắt ướt và bán kính thủy lực
• C – Số Chezy
RiCV
iKRiACQ
löôïng löu module - RACK
Cho 5 thông số, hỏi thông số còn lại (hoặc hỏi
2 thông số thì phải cho thêm 1 điều kiện)
61
1
/
R
n
C
Công thức Manning
2.2
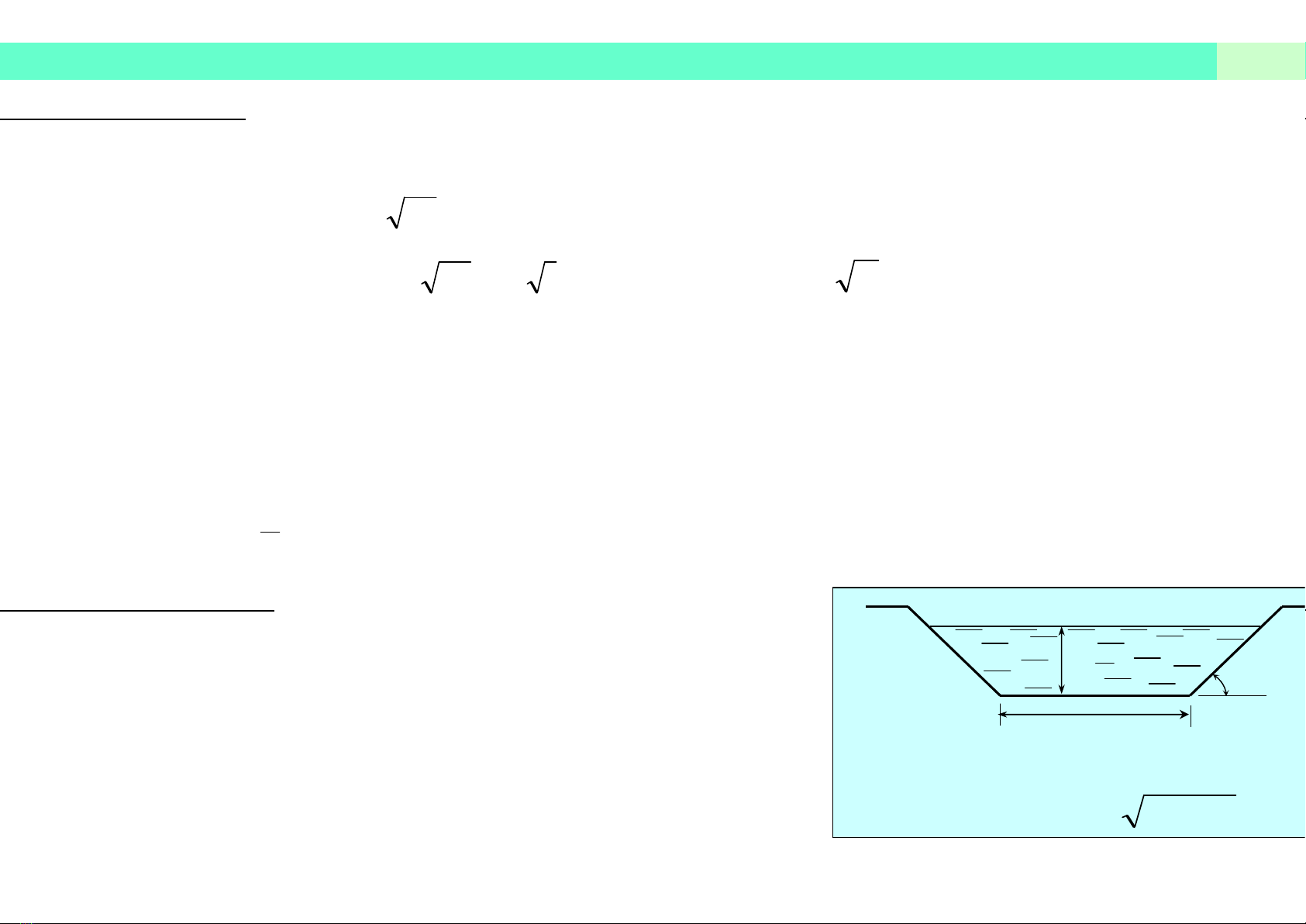
Các bài toán cơ bản (xét kênh hình thang)
Phân
tích:
Số ptrình: 1 (cthức Chezy)
Số thông số: 6 (b, h, m, n, i, Q)
h
b
m
2
12 mhbP
mhbhA
Pgs.Ts
121
2. T
ÍNH TOÁN DÒNG CHẢY ĐỀU TRONG KÊNH HỞ (2/7)
a.
Bài toán 1
Bài toán: Cho b, h, m, n. Biết i hỏi Q (hoặc biết Q hỏi i)
Cách giải:
• Tính A, P R
• Tính C K
• Tính
iKQ
22 KQi hoaëc
V
í dụ: Kênh lăng trụ mặt cắt hình thang có b=20m, h=4m, m=1, n=0,020, i=0,0001. Hỏi Q?
Gi
ải
2
964.1204 mmmmhbhA
mmmmhbP 31,3111.4.22012
22
m
m
m
P
A
R066,3
31,31
96 2
smR
n
C5,06/16/1 26,60066,3
020,0
11
smmsmmRCAK 35,02 10130066,3.26,60.96..
smsmiKQ 33 30,1010001,0.10130
Pgs.Ts
122
2. T
ÍNH TOÁN DÒNG CHẢY ĐỀU TRONG KÊNH HỞ (3/7)
V
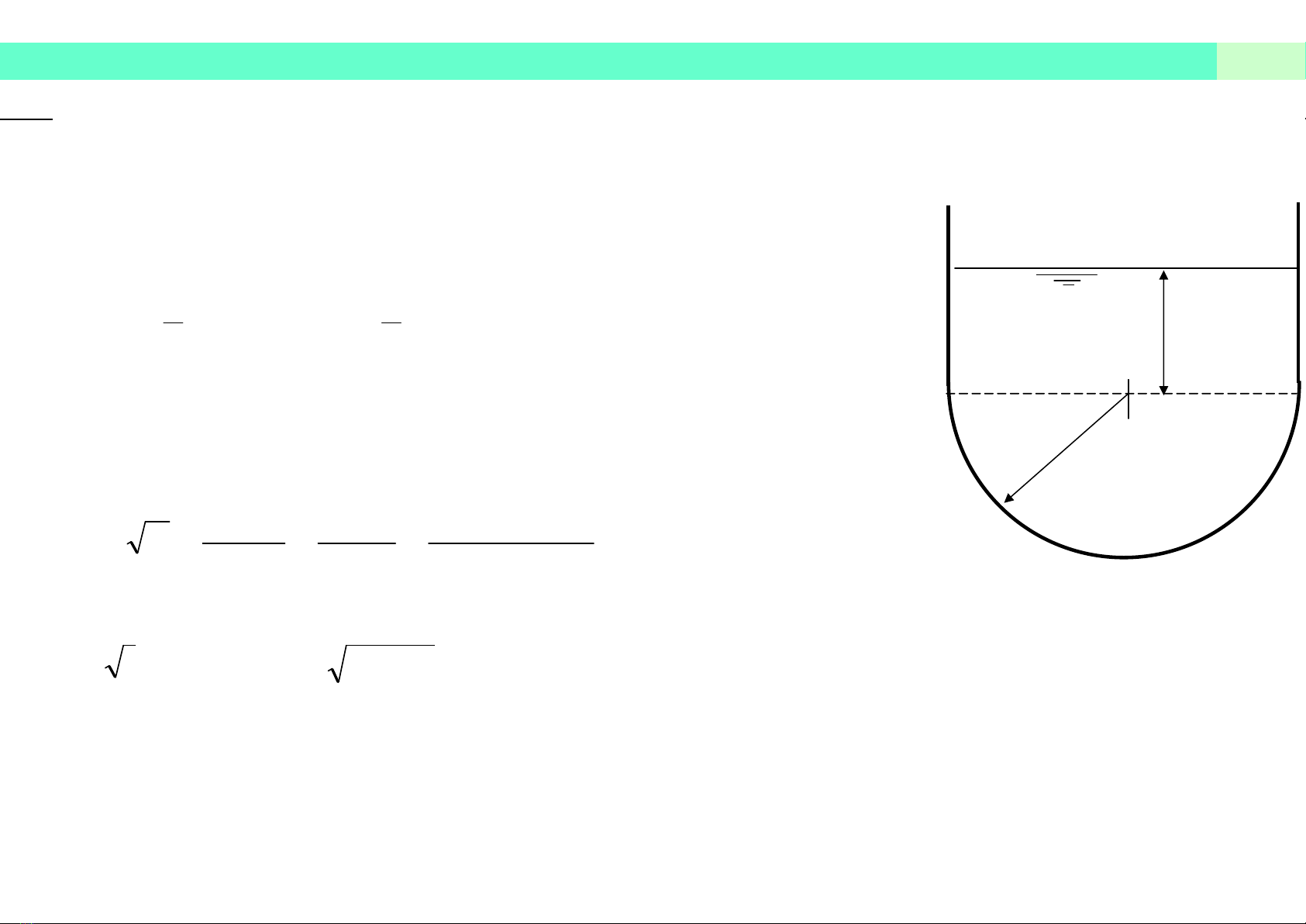
í dụ: Kênh lăng trụ mặt cắt ngang như hình vẽ. Biết R=5m, h=2m, n=0,020, i=0,0004. Hỏi Q?
Gi
ải
2
2
227.595
2
1
2.5.2
2
1
.2 mmmRhRA
mmmRhP 7,195.2.22
sm
Pn
A
n
RA
RACK /2,6176
7,19.02,0
27,59
.
.3
3/2
3/5
3/2
3/53/2
smsmiKQ /52,1230004,0./2,6176 33
R
h
Pgs.Ts
