DepartmentofAppliedMechanics
CHAPTER Cơhọckỹthuật: ĐỘNGLỰCHỌC
EngineeringMechanics:KINETICS
Độnglựchọc:Vachạm
BộmônCơhọcứngdụng
DepartmentofAppliedMechanics
Cơhọckỹthuật
ĐỘNGLỰCHỌC
EngineeringMechanics
KINETICS
ĐỘNGLỰCHỌC:VACHẠM
BộmônCơhọcứngdụng
GV:……………………………………..
DepartmentofAppliedMechanics 3
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
CÁCGIẢTHIẾTVÀCÁCĐỊNHLÝĐỐIVỚIBÀITOÁNVACHẠM
1. Địnhnghĩavàvídụ
2. Đặcđiểmvàcácgiảthiết
3. Môhìnhcơ họchaivậtphẳngvanhau
4. ĐịnhlýNewtonvàĐịnhlýPoissonvềvachạm
5. Địnhlýđộnglượngvàmômenđộnglượngtrongvachạm
DepartmentofAppliedMechanics 4
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
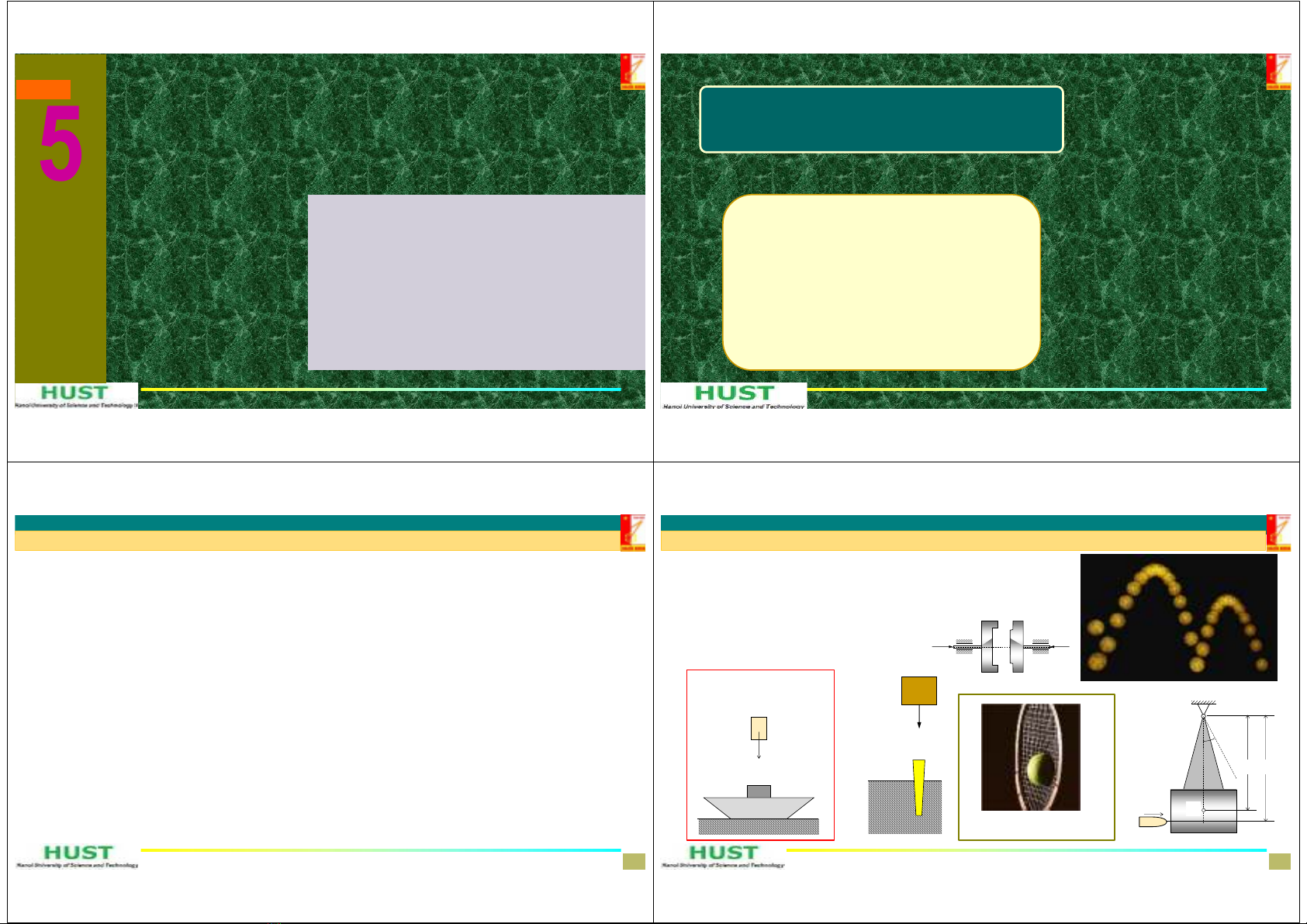
1.Địnhnghĩavàvídụ
vachạm(tươngtácphức
tạp)
https://en.wikipedia.org/wiki/Inelastic_collision
v1
m1
m2
Đóngcọc,
đóngđinh
Rèn
m1
phôi+đe
v1
a
C
O
h
v
m0
Conlắcđo
vậntốcviên
đạn
Định nghĩa: Va chạm của các vật rắn là sự tiếp xúc bất thình
lình của các vật rắn, gây nên sự thay đổi vận tốc các điểm và
vận tốc góc của các vật rắn một lượng hữu hạn trong một
khoảng thời gian rất bé.
Một số ví dụ FF
I1I2
12
DepartmentofAppliedMechanics 5
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
2.Đặcđiểmvàcácgiảthiết
Đặc điểm
vachạm(tươngtác
phứctạp) Sauvachạm
Trướcvachạm
1212
,,
CC C
ttt t ttt
•Thờigianvachạm:t=t2‐t
1rấtnhỏ
•Giaiđoạnbiếndạngvàgiaiđoạnphụchồi(khôi
phục)
2
1
2
1
()
() ()
C
C
t
t
tt
tt
SRtdt
R t dt R t dt




tt1t2
tC
R(t) S
•Lựcvachạm,Xunglựcvachạm
C1
1
P
2
C2
1
v
2
v
R
R
•vachạmmềm(tC=t2)
•vachạmđànhồi
•vachạmtuyệtđốiđànhồi
(khôiphụchoàntoàn
đượchìnhdángbanđầu)
DepartmentofAppliedMechanics 6
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
2.Đặcđiểmvàcácgiảthiết
Các giả thiết gần đúng
Diện tích tiếp xúc nhỏ (coi như tiếp xúc điểm)
Trong quá trình va chạm vị trí củacácvậtvanhaucoi như
không đổi,dothờigianvachạmt=t
2‐t
1rất bé.
Các lực va chạm lớn tới mức có thể bỏ qua tác dụng của các
lực thông thường (trọng lượng, sức đẩy của gió, lực cản
không khí, ...) trong thời gian va chạm.
n
C1
Đườngva
chạm
Mặtphẳngtiếp
xúcchung
1
P
2
C2
2n
v
1n
v
1
v
2
v
C1
1
P
2
C2
1
v
2
v
R
R
DepartmentofAppliedMechanics 7
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
3.Môhìnhcơ họchaivậtrắnphẳngvanhau
12
,vv
 vậntốccủahaiđiểmP1vàP2tạiđiểmtiếpxúctrướcvachạm.
12
,vv

 vậntốccủahaiđiểmP1vàP2tạiđiểmtiếpxúcsauvachạm.
12
12
,,
,
nn
nn
vv
vv

hìnhchiếuvậntốccủahaiđiểmP1vàP2tạiđiểmtiếpxúc
trướcvàsauvachạmtrênđườngvachạmn.
C1
P1
P2
C2
n
n
R
R
R
n
R
n
C1
Đườngva
chạm
Mặtphẳngtiếp
xúcchung
1E
P
2
C2
2n
v
1n
v
1
v
2
v
Lựcvachạm
tt1t2
tC
Rn(t)
•Vachạmnhẵn
•Vachạmkhôngnhẵn(nhám)
0R
0R
Lưu ý chiều của thành phần tt Rt
DepartmentofAppliedMechanics 8
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
3.Môhìnhcơ họchaivậtrắnphẳngvanhau/phânloại
C1C2
n
Va chạm xuyên tâm:đườngva
chạm trùng đường nối qua hai
khối tâm. Trái lại là va chạm
không xuyên tâm.
n
C1
Đườngva
chạm
1
P
2
C2
vckhôngxuyên
tâm
vcxuyêntâm
n
C1
Đườngva
chạm
1
P
2
C2
1
v
2
v
Va chạm thẳng:vậntốchaiđiểm
va nhau nằm trên đường va
chạm. Trái lại là va chạm xiên.
n
C1
Đườngva
chạm
1
P
2
C2
1
v
2
v
vcthẳng
vcxiên
C1
P1
P2
C2
n
n
R
n
R
C1
P1
P2
C2
n
n
R
R
R
n
R
Vachạmnhẵn vàvachạm
khôngnhẵn(nhám)
vcnhẵn
vckhôngnhẵn
DepartmentofAppliedMechanics 9
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
4.ĐịnhluậtNewtonvàĐịnhluậtPoissonvềvachạm
ĐịnhluậtNewtonvềvachạm
21
21
nn
nn
vv
evv

2
1
2
12
1
, ( ) , ( )
C
C
tt
tt
S
eSRtdtSRtdt
S


C1
P1
P2
C2
n
n
R
R
R
n
R
n
C1
Đườngva
chạm
1
P
2
C2
2n
v
1n
v
1
v
2
v
Lưu ý: khi áp dụng chỉ cần sử dụng một trong hai định luật trên.
vachạmmềm,khôngcógiaiđoạnkhôiphục;
0
01
1
e
e
e

vachạmtuyệtđốiđànhồi,(khônghaotổnnăng
lượng).
vachạmđànhồi;
Cặpvậtliệu Hệsốvachạme
Gỗ‐Gỗ 0.5
Thép‐Thép 0.60.8
Ngàvoi‐Ngàvoi 0.89
Thủytinh‐Thủytinh 0.94
Ref.Gross,etal.
Phânloạivachạmcăncứvàohằngsốvachạm
ĐịnhluậtPoissonvềvachạm
2
1
n
n
S
eS
Đốivớiva
chạmnhẵn
DepartmentofAppliedMechanics 10
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
5.Cácđịnhlýbiếnthiênđộnglượngvàmômenđộnglượngtrongvachạm
0
() (0) ()
ee
kk
pp S Rtdt



Địnhlýbiếnthiênđộnglượng
ĐiểmOcốđịnh
00
00
0
() (0) ( ) () ()
() (0) ( ) () ()
() (0) ( ) ( ())
ee e
OO Ok kk k k
ee e
CC Ck kk k k
ee
zz zk zk
ll mS rRtdtrRtdt
ll mS uRtdtuRtdt
ll mS mRtdt












Địnhlýbiếnthiênmômenđộnglượng
C1
P1
P2
C2
n
n
R
R
R
n
R
Trụczcốđịnh
Clàkhốitâm(vậthoặchệ).
Lưuý:cácđịnhlýnàyđượcápdụngchotừngvậthoặccảhệ.
Tạisaotrongquátrìnhvachạmtakhôngápdụngphươngphápnănglượng?
DepartmentofAppliedMechanics 11
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
VACHẠMCỦAHAIVẬTTỊNHTIẾN
1.Vachạmthẳngxuyêntâmcủahaivậttịnhtiến
Đặtbàitoán
Phântíchvàtínhtoán
Vídụ
2.Vachạmxiêncủahaivậttịnhtiến
DepartmentofAppliedMechanics 12
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
1.Vachạmthẳngxuyêntâm/a.Đặtbàitoán
Ta xét hai quả cầu đồng chất khối lượng m1và m2. Chúng chuyển động tịnh tiến theo đường thẳng xuyên
tâm với các vận tốc v1và v2(v1>v
2) và va chạm nhau. Cho biết hệ số khôi phục là e.
Tìm các vận tốc sau va chạm v’1và v’2; lượng mất động năng T qua va chạm của hai quả cầu.
1
tt21
tt

1
v
1
m
2
v
2
m
12
vv
1
v
2
v
1
v
2
v
1
v
2
v
12
vv

Quátrìnhvachạm
DepartmentofAppliedMechanics 13
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
1.Vachạmthẳngxuyêntâm/b.Phântíchvàtínhtoán
Quátrìnhvachạmđượcphânthànhpha: biếndạngvàphakhôiphục
10tC
t2
t
1
v
1
m
2
v
2
m
u
1
v
2
v
phabiếndạng phakhôiphục
t
Quátrìnhvachạm
R
R
1
m2
m
Lựcvachạm
tt1t2
tC
R(t)
S2
S1
Độnglượng:
11 22
(0)pmvmv

12
() ( )
C
pt m m u

21122
()pt mv mv



DepartmentofAppliedMechanics 14
Vachạmgiữacácvậtrắn‐Collisionofrigidbodies
1.Vachạmthẳngxuyêntâm/b.Phântíchvàtínhtoán
10tC
t2
t
1
v
1
m
2
v
2
m
u
1
v
2
v
t
Độnglượng:
11122
()pt mv mv

12
() ( )
C
pt m m u

21122
()pt mv mv



Khixétcảhệđộnglượngđượcbảotoàn:
12
() ( ) ()
C
pt pt pt

HệsốvachạmNewton 21
21
vv
evv


11 22 11 22 1 2
()mv mv mv mv m m u


21 12
()vvevv


(1)
(2)
Giảihệ(1)và(2)tanhậnđược
11 22
12
2
11 12
12
1
22 12
12
(1 ) ( )
(1 ) ( )
mv mv
umm
m
vv e vv
mm
m
vv e vv
mm


DepartmentofAppliedMechanics 15
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
1.Vachạmthẳngxuyêntâm/b.Phântíchvàtínhtoán
Đểtínhxunglựcvachạmtaápdụngđịnhlýbiến
thiênđộnglượngchomỗiquảcầu
trongphabiếndạng: S
1
m2
m
S
trongphakhôiphục
1111
mu mv S
11 1 2
mv mu S

2221
mu mv S
22 2 2
mv mu S

TínhhệsốvachạmtheoPoisson
212 21
112 21
()()
()()
Svv vv
eSvv vv




Vậtm1
Vậtm2
Vậtm1
Vậtm2
(2)
(1)
(4)
(3)
Nhân(2)vớim1trừđi(1)nhânm2tađược:
121 2
1
12
()
()
mm v v
Smm
Nhân(4)vớim1trừđi(3)nhânm2tađược:
121 2
2
12
()
()
mm v v
Smm


VậyhệsốvachạmtheoPoissonvàNewtonlànhưnhau.
DepartmentofAppliedMechanics 16
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
1.Vachạmthẳngxuyêntâm/b.Phântíchvàtínhtoán
Lượngmấtđộngnăngquavachạm
10t
C
t2
t
1
v
1
m
2
v
2
m
u
1
v
2
v
t
12
2
11 12
12
1
22 12
12
,
(1 ) ( )
(1 ) ( )
vv
m
vv e vv
mm
m
vv e vv
mm



22 2 2
11 22 11 22
22 22
11 1 22 2
2
2
12
12
12
11
22
11
()()
22
1()
2
tvc svc
TT T mv mv mv mv
mv v mv v
mm
evv
mm





Nănglượngnàychuyểnhóađiđâu?
10
01 0
eT
eT


DepartmentofAppliedMechanics 17
Vachạmgiữacácvậtrắn‐Collisionofrigidbodies
1.Vachạmthẳngxuyêntâm/c.Hiệusuấtđóngcọcvàhiệusuấtrèn
2
2
12
1
12
1
2
tvc svc
mm
e
TT T v
mm

Ápdụngvàobàitoánrèn
Búam1,v1;phôi+đe:m2,v2=0 11 22 12
,, , 0 ,mv mv vv


Đểphôibiếndạngnhiều,yêucầuTlớnvà v’2nhỏ0.
Hiệusuấtvađậpkhirènđượctính
2
2
12
(1 )
tvc
me
T
Tmm

2
11
1
2
tvc
Tmv
Đểcóhiệusuấtrèncaotacầnchọn
(đephảilớn) 21
mm
Rèn
m1
m2:phôi+đe
v1
DepartmentofAppliedMechanics 18
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
1.Vachạmthẳngxuyêntâm/c.Hiệusuấtđóngcọcvàhiệusuấtrèn
1
21
12
(1 ) m
ve v
mm

v1
m1
m2
Đóngcọc,
đóngđinh
Ápdụngvàobàitoánđóngđinh,đóngcọc:
Búam1,v1cọc(đinh):m2,v2=0 11 22 12
,, , 0 ,mv mv vv


Yêucầuv’2lớn(đểcọc/đinhlúnsâu)
Đểcóhiệuquảđóngcọccaotacầnchọn 12
mm
1
22 12
12
(1 ) ( )
m
vv e vv
mm

DepartmentofAppliedMechanics 19
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
1.Vachạmthẳngxuyêntâm/d.Xácđịnhhệsốvachạmbằngthựcnghiệm
Từ độ cao h0= 36 cm một quả cầu nhỏ rơi xuống nền ngang nhẵn
rồi nẩy lên như trên hình. Đo được độ cao h1=32cm.Hãyxác
định: (a) hệ số khôi phục e,(b)độcaoh2.
2
1
00
22mv mgh v gh
‐ Xácđịnhvậntốcquảcầunhỏtrướcvachạmtừh0.
1
2vgh
‐ Xácđịnhvậntốcquảcầunhỏsauvachạmtừh1.
h0h1h2h3
d1d2d3
n
‐ ÁpdụngđịnhluậtNewtonvềvachạm
21
21
0
0
nn
nn
vv vv
evv vv



 

Hướngdẫn
11
0
0
20.943
2
gh h
v
evh
gh

(a)hệsốkhôiphụce
(b)độcaoh2.
2
12
21
01
28.44
hh
eheh
hh

DepartmentofAppliedMechanics 20
Vachạmgiữacácvậtrắn‐ Collisionofrigidbodies
2.Vachạmxiêncủahaivậttịnhtiến
n
t
v1
v2
u2
u1
m1
m2
Phân tích các vận tốc thành hai thành phần vuông góc: một thành phần
pháp tuyến n(đường nối khối tâm hai vật) và một thành phần tiếp tuyến t:
Thành phần tiếp tuyến của vận tốc không đổi qua va chạm
11 22
;
tt tt
vu vu
11 22 1 1 2 2
nn n n
mv mv mu mu
22 2 2
11 12 1 1 1 2
11
()( )
22
tvc svc
TT T
mv mv mu mu


21
21
nn
nn
uu
evv

ĐịnhluậtNewtonvềvachạm
Bảotoànđộnglượngcủa2vậttheophươngpháptuyến
(1)
(2)
(3)
Giảihệ(1,2,3)tìmđượcthànhphầnvậntốcsauvachạm
121 2 12
,, , ,
ttnn
uuu u uu
Lượngmấtđộngnăngquavachạm
Bàitoán:chom1,m2,v1,v2,e.Tìmu1,u2,T. Vachạmnhẵn