DepartmentofAppliedMechanics
CHAPTER Cơhọckỹthuật: ĐỘNGLỰCHỌC
EngineeringMechanics:KINETICS
Độnglựchọc:
xunglực– độnglượng
BộmônCơhọcứngdụng
DepartmentofAppliedMechanics
Cơhọckỹthuật
ĐỘNGLỰCHỌC
EngineeringMechanics
KINETICS
ĐỘNGLỰCHỌC:
XUNGLỰC– ĐỘNGLƯỢNG
BộmônCơhọcứngdụng
GV:……………………………………..
DepartmentofAppliedMechanics 3
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
XUNGLỰC– ĐỘNGLƯỢNG– ĐỊNHLÝBIẾNTHIÊNĐỘNGLƯỢNG
1. Địnhnghĩa:Xunglực,độnglượng
2. Địnhlýbiếnthiênđộnglượng
3. Địnhlýbảotoànđộnglượng
4. Vídụápdụng
DepartmentofAppliedMechanics 4
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
1.Địnhnghĩa:Xunglực,độnglượng
()dS F t dt
Xunglượng(Xunglực,Xunglượngcủalực):làđạilượngvéctơđặctrưngtácdụngcủalựctheo
thờigian.
XunglượngcủalựcF(t)trongkhoảngthờigiandt,kíhiệudS
XunglượngcủalựcF(t)trongkhoảngthờigianhữuhạntừt1đếnt2:
2
1
()
t
t
SFtdt

tt1t2
F(t)
S
ĐơnvịcủaxunglựclàNewton‐giây[N.s]
DepartmentofAppliedMechanics 5
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
1.Địnhnghĩa:Xunglực,độnglượng
pmv
Động lượng được hiểu đơn giản là khối lượng trong chuyển động (hay đà
chuyển động). Động lượng càng của vật càng lớn thì càng khó dừng lại.
Động lượng là đại lượng véc tơ bằng tích của khối lượng với véc
tơ vận tốc của nó
11 1
() ,
nn n
kk k C C k
kk k
pmv mvmvmm




[kg.m/s]
m
O()rt
v
p
k
x
k
y
k
z
x
y
z
mk
O
m1
kk
mv
Độnglượngcủahệnchấtđiểmbằngtổnghìnhhọc
độnglượngcủacácchấtđiểm
DepartmentofAppliedMechanics 6
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
1.Địnhnghĩa:Xunglực,độnglượng
CC
pvdmrdmmrmv




Động lượng của vật rắn
11 11
11
pp
nn
kk iCi k i C C
ki ki
p
n
ki
ki
pmv mv m mvmv
mm m










Độnglượngcủacơ hệ(cácvậtrắnvàcácchấtđiểm)
b)
x
y
z
O
C
x
y
z
vdm
r
C
r
u
xy
z
O
C
Ci
i
C
r
k
r
k
u
Ci
u
C
r
k
m
i
m
DepartmentofAppliedMechanics 7
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
1.Địnhnghĩa:Xunglực,độnglượng
Động lượng của cơ hệ
11 11
11 11
11 11
pp
nn
x kkiCi kiCC
ki ki
pp
nn
ykkiCi kiCC
ki ki
pp
nn
z kkiCi kiCC
ki ki
pmxmx mmxmx
pmymy mmymy
pmzmz mmzmz





















xy
z
O
C
Ci
i
C
r
k
r
k
u
Ci
u
C
r
k
m
i
m
11 11
pp
nn
kk iCi k i C C
ki ki
pmv mv m mvmv







trong hệ tọa độ Đề ‐các
DepartmentofAppliedMechanics 8
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
2.Địnhlýbiếnthiênđộnglượng
Xuấtpháttừđịnhluật2Newton
2
1
21
() () () () t
kt
dmv F F d mv Fdt dS mv t mv t S Fdt
dt 


a)Đốivớichấtđiểm
Địnhlý1.Viphânđộnglượngcủachấtđiểmbằngxunglựcnguyêntốcủahợplựccủacáclựctácdụng
lênchấtđiểmđó.
Định lý 2. Biến thiên động lượng của chất điểm trong một khoảng thời gian nào đó bằng tổng hình học
xung lượng của các lực tác dụng lên chất điểm trong thời gian ấy.
1
()mv t
2
1
t
tFdt
2
()mv t
Địnhlý1 Địnhlý2
DepartmentofAppliedMechanics 9
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
2.Địnhlýbiếnthiênđộnglượng
b)Đốivớicơhệ
Địnhlý3.Đạohàmtheothờigianđộnglượngcủa
cơhệbằngvéctơchínhcủacácngoạilựctácdụng
lêncơhệ.
Định lý 4. Vi phân động lượng của cơ hệ bằng tổng
hình học xung lượng nguyên tố của các ngoại lực tác
dụng lên cơ hệ.
Định lý 5. Biến thiên động lượng của cơ hệ
trong một khoảng thời gian nào đó bằng tổng
hình học xung lượng của các ngoại lực tác dụng
lên cơ hệ trong khoảng thời gian ấy.
Lưuý:khôngthấysựcómặtcủanộilựctrongđịnhlýđộng
lượng.Nộilựckhônglàmbiếnđổiđộnglượngcủahệ.
e
k
k
dp F
dt 
ee
kk
kk
dp dS F dt


2
1
21
() () t
ee
kk
t
kk
pt pt S Fdt



1
()
C
mv t
2
1
te
k
tFdt
2
()
C
mv t
e
Ck
k
ma F
DepartmentofAppliedMechanics 10
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
3.Địnhlýbảotoànđộnglượng
0,
e
kC
k
If F p const mv const
Địnhlý6:Nếuvectơchínhcủacácngoạilựctácdụnglêncơhệluônluônbằngkhôngthìđộnglượngcủa
cơhệđượcbảotoàn.
Địnhlý7: Nếuhìnhchiếucủavectơchínhcủacácngoạilựclênmộttrụcnàođóluônluônbằngkhôngthì
hìnhchiếuđộnglượngcủacơhệlêntrụcấyđượcbảotoàn.
0,
e
kx x C
k
If F p const mx const
DepartmentofAppliedMechanics 11
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
4.Vídụápdụng
Lực phụ thuộc thời gian P(t)
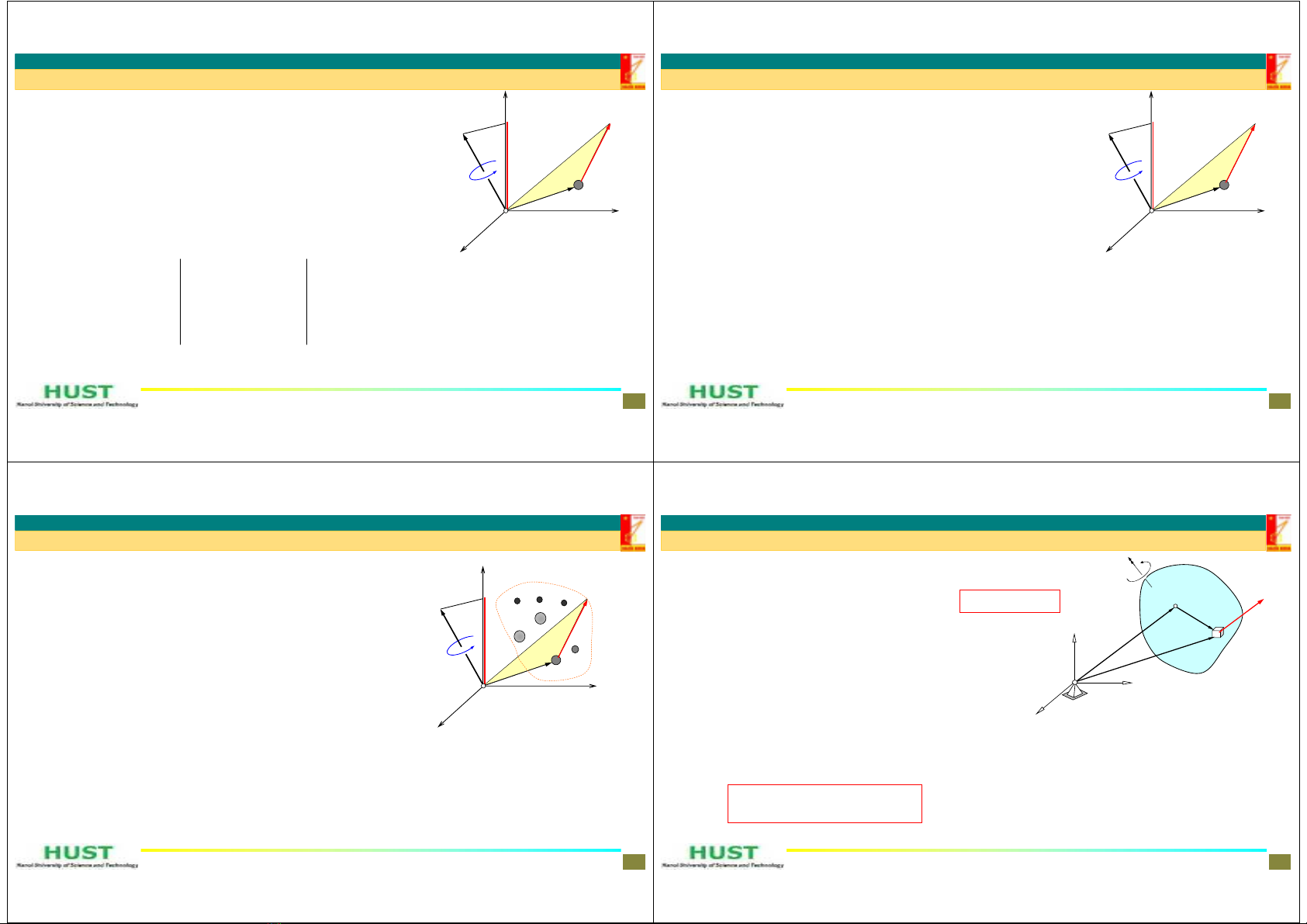
Ví dụ 1. Xeôtôkhốilượngmkhởi động trên đường thẳng ngang từ
trạngtháiđứngyêndolựcđẩyP=P
0(1‐exp(‐a.t)), với P0,alàconst.
Bỏ qua lực cản. Tìm biểu thức vận tốc của xe là hàm theo thời gian.
m
P
t
xx x x x
d mv F dt mv t mv F dt v
0
( ) ( ) (0) , (0) 0
Lời giải.
Lực phụ thuộc thời gian, nên áp dụng định lý động lượng.
Ở đây chỉ quan tâm phương ngang x.
tt
at at
at
PedtPtea
Pt e a P a
00
0
0
00
(1 ) ( / )
(/)/



t
xx x
tat
x
mv t mv F dt
mv P e dt
0
0
0
() (0)
(0) (1 )



at
xx
vt v Pt e a P a
m00
1
() (0) ( / ) /

x
y
DepartmentofAppliedMechanics 12
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
4.Vídụápdụng
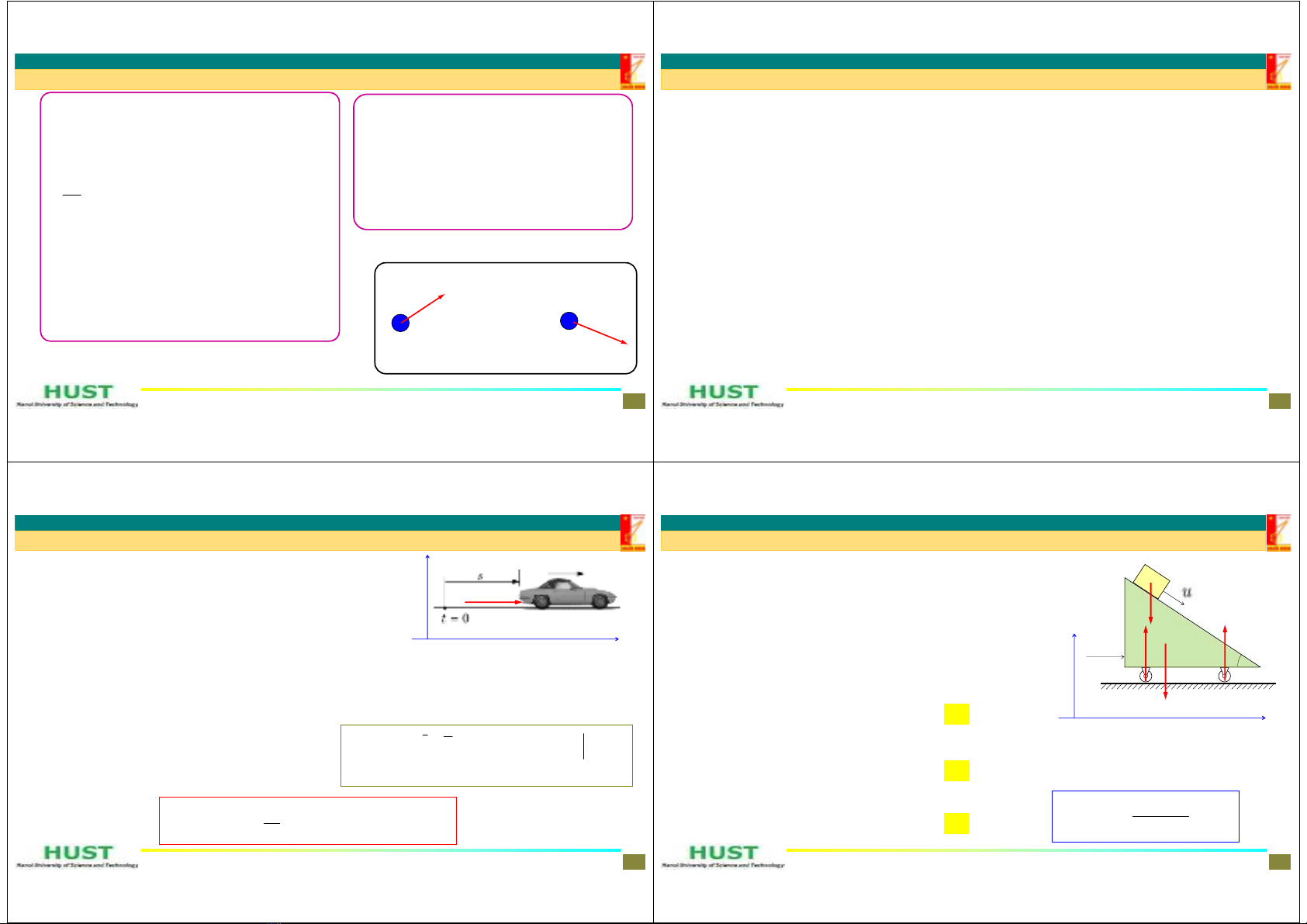
Vídụ2.Bảotoànđộnglượng.ChocơhệgồmvậtAcókhốilượngm1đặt
trênmặtnghiêngcủamộtlăngtrụcókhốilượngm2.Gócnghiêngcủa
mặtlăngtrụvớimặtphẳngnganglà.Lăngtrụđượcđặttrênmộtmặt
ngangnhẵnnhưhìnhvẽ.Banđầuvậtnặngnằmyêntươngđốitrênmặt
lăngtrụ,cònchínhlăngtrụthìtrượtngangsangphảivớivậntốcv0.Sau
đóchovậtAtrượtxuốngtheomặtphẳngnghiêngcủalăngtrụvớivận
tốctươngđốiu=at.Tìmvậntốccủalăngtrụ.
v0
u
A
m1
m2
m
vv u
mm
1
0
12
cos a= - +
HD: Các ngoại lực tác dụng lên hệ: P1,P
2,N
1,N
2
e
kx x x
Fpconstp
,0(0)å== =
xxx
pmv mv
mmv
11 22
120
(0) (0) (0)
()


(1)
(2)
xxx
pt mv t mv t
mvt u mvt
11 22
12
() () ()
(() cos ) ()a
=+
=+ + (3)
x
y
P2
P1
N1
N2
DepartmentofAppliedMechanics 13
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
4.Vídụápdụng
Ví dụ 3. Vật nặng A khối lượng 100‐kg được thả từ trạng thái đứng yên.Nếu
bỏ qua khối lượng các puli và dây, hãy xác định vận tốc của vật nặng B khối
lượng 20 kg sau thời gian 2 giây. (g = 9.81 m/s2)
A
C
O
B
D
sAsB
Lờigiải
Sơđồgiảiphóngliênkết(Sơđồvậtthểtựdo)
WA
2T
2T
TT
A
WB
T
B
VậtA: 2
0
(0)(1009.812)
AA
mv Tdt
2
0
( 0) (20 9.81 )
BB
mv Tdt
Ápdụngđịnhlýđộnglượngtrongkhoảngthờigian2s:
(1)
(2)Vật B:
220
AB AB
ss l vv
Ràng buộc động học
(3)
2
0 654.0Nms, 6.54 m/ s, 13.08 m/ s.
AB
Tdt v v
DepartmentofAppliedMechanics 14
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
Mộtsốbàitoánsửdụngphươngphápđộnglượng
1. Khilực/mômenlàhàmcủathờigian.Xácđịnhđượcvậntốctheothờigian
2. Khihệcókhốilượngthayđổi(tênlửa– rocket)
3. Bàitoánvachạm
Lưuýrằng,phươngpháplực‐giatốccũngđượcsuyratừphươngphápđộnglượngkhikhối
lượngkhôngđổi.
vachạm(tươngtác
phứctạp) Sauvachạm
Trướcvachạm
DepartmentofAppliedMechanics 15
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
ĐỊNHLÝBIẾNTHIÊNMÔMENĐỘNGLƯỢNG
1. Mômenxunglực,mômenđộnglượng
2. Địnhlýbiếnthiênmômenđộnglượng
3. Địnhlýbảotoànmômenđộnglượng
4. Vídụápdụng
DepartmentofAppliedMechanics 16
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
1.Địnhnghĩa:Mômenxunglực,mômenđộnglượng
O
dK m F dt r Fdt()


Mômen xung lượng (mômen xung lượng của lực): là đại
lượng véc tơ đặc trưng tác dụng của ngẫu lực / mômen
của lực theo thời gian.
Mômen xung lượng của lực F(t) đối với điểm O (trục z)
trong khoảng thời gian dt,kíhiệudK
MômenxunglượngcủalựcF(t)trongkhoảngthờigianhữuhạntừt1đếnt2:
tt
O
tt
KmFdtrFdt
22
11
()



tt1t2
mO(t)
K
ĐơnvịcủamômenxunglựclàNewton‐mét‐giây[N.m.s]
zz z
dK m F dt u r F dt() ( )


tt
zz z
tt
KmFdturFdt
22
11
() ( )



F
z
x
y
r
A
O
xyz
eee{, , }

O
mF()
Oz
m
DepartmentofAppliedMechanics 17
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
1.Địnhnghĩa:Mômenxunglực,mômenđộnglượng
OO
lmmvrmv()


MômenđộnglượngcủachấtđiểmđốivớimộttâmO
[kg.m2/s]
xyz xxyyzz
OOxxOyyOzz
rxe ye ze vve ve ve
llelele
,



TínhtoántronghệOxyzvớicơ sở
xyz
O
xyz
zyx x zy y xz
eee
lrmv x y z
mv mv mv
myv zv e mzv xv e mxv yv e
()
()()()




xyz
eee{, , }
 mv
z
x
y
r
A
O
xyz
eee{, , }

O
l
Oz
l
DepartmentofAppliedMechanics 18
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
MômenđộnglượngcủachấtđiểmđốivớimộttrụczquaO
Oz Oz z O z
lmmvelermv() ( )


O
zyx x zy
yxz
lrmv
myv zv e mzv xv e
mxv yv e
()
()()
()




mv
z
x
y
r
A
O
xyz
eee{, , }

O
l
Oz
l
Ox x O x z y
Oy y O y x z
Oz z O z y x
lmmvlemyvzv
lmmvlemzvxv
lmmvlemxvyv
() ( )
() ( )
() ( )



1.Địnhnghĩa:Mômenxunglực,mômenđộnglượng
DepartmentofAppliedMechanics 19
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
1.Địnhnghĩa:Mômenxunglực,mômenđộnglượng
MômenđộnglượngcủahệchấtđiểmđốivớimộttâmO/đốivớitrụcOz
kk
mv
z
x
y
rk
A
O
xyz
eee{, , }

O
l
Oz
l
nnn
OOkkkkkk
kkk
nn
Oz z k z k k
kk
n
Oz z k z O O z
k
lmp rprmv
lmpmmv
lmphclle
111
11
1
()
() ( )
() ()










DepartmentofAppliedMechanics 20
Độnglựchọccơ hệ:Xunglực– độnglượng.Kineticsofamechanicalsystems:Impulse‐ momentum
1.Địnhnghĩa:Mômenxunglực,mômenđộnglượng
C
vv uw=+´
MômenđộnglượngcủavậtrắnđốivớikhốitâmCcủanó
CC
uvdm udmv udm0, 0´= ´= =
òò ò


C
O
vdm
w
r
C
r
u
CC
C
C
lmvdmuvdm
uv udm
uvdm u udm
()
()
()
w
w
==´
=´+´
=´ +´´
ò
ò
ò
ò
ò


C
lu udm()w=´´
ò
