DepartmentofAppliedMechanics
CHAPTER Cơhọckỹthuật: ĐỘNGLỰCHỌC
EngineeringMechanics:KINETICS
Độnglựchọc:lực– giatốc
BộmônCơhọcứngdụng
DepartmentofAppliedMechanics
Cơhọckỹthuật
ĐỘNGLỰCHỌC
EngineeringMechanics
KINETICS
ĐỘNGLỰCHỌC:LỰC– GIATỐC
BộmônCơhọcứngdụng
GV:……………………………………..
DepartmentofAppliedMechanics 3
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
ĐỘNGLỰCHỌCCHẤTĐIỂM:Lực–giatốc
1. Phươngtrìnhviphânchuyểnđộngcủachấtđiểm
•Tọađộđềcác
•Tọađộtựnhiên
•Tọađộcực
•Tọađộtrụ
2. Cácbàitoáncơbảncủađộnglựchọc
3. Mộtsốvídụ
DepartmentofAppliedMechanics 4
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
Xuấtpháttừđịnhluật2Newton
() , (,,)
k
dmv F F m const ma F r v t
dt 



Trong hệ tọa độ đề các Oxyz cố định:
,(,,)
xyz xxyyzz
axeyeze FrvtFeFeFe

  
x
y
z
mx F
my F
mz F



xxyyzz
xxyyzz
000
000
(0) , (0) , (0)
(0) , (0) , (0)



x
e
z
e
y
e
m
r
x
z
y
O
F
PTVP CĐ trong hệ tọa độ đề các
Cácđiềukiệnđầuvềvịtrívàvậntốc
1.Phươngtrìnhviphânchuyểnđộngcủachấtđiểm
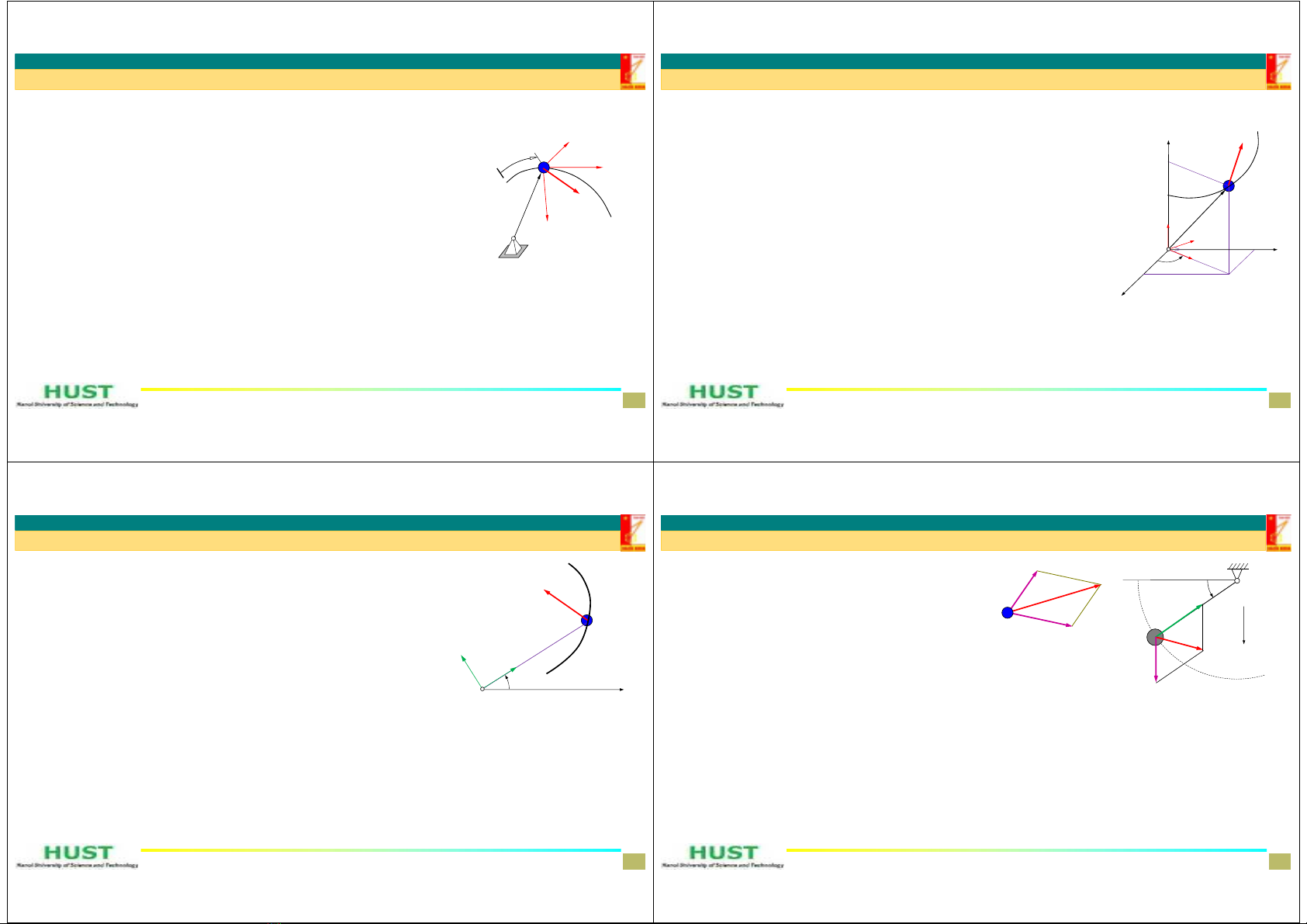
DepartmentofAppliedMechanics 5
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
1.Phươngtrình viphânchuyểnđộngcủachấtđiểm
PTVPCĐcủachấtđiểmtrongdạngtọađộtựnhiên
O
s(t)ds
r
P0
t
e
b
e
n
e
m
F
2
:, (/)
tn t t n n
aa a a se a s e



2
,/,0
tnb
asv a s a


2
,
/,
0
t
n
b
ms F
mv F
mF


00
(0) , (0)ss sv
Cácđiềukiệnđầuvềvịtrívàvậntốc
DepartmentofAppliedMechanics 6
Độnglựchọccơhệ:Lực–giatốc.Kineticsofamechanicalsystems:Force‐acceleration
1.Phươngtrình viphânchuyểnđộngcủachấtđiểm
PTVPCĐcủachấtđiểmtrongdạngtọađộtrụ
2
()(2)
rz
rr zz
av rr e r re ze
FFe Fe Fe






 

2
(),
(2),
r
z
mr r F
mr r F
mz F






00
00
00
(0) , (0)
(0) , (0)
(0) , (0)
rr rr
zz zz






Cácđiềukiệnđầuvềvịtrívàvậntốc
m
F
r
OyM
zM
xM
z
r
z
e
r
e
e
DepartmentofAppliedMechanics 7
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
1.Phươngtrình viphânchuyểnđộngcủachấtđiểm
PTVPCĐcủachấtđiểmtrongdạngtọađộcực
2
()(2)
r
rr
av rre r re
FFe Fe








2
(),
(2),
r
mr r F
mr r F





00
00
(0) , (0)
(0) , (0)
rr rr





Cácđiềukiệnđầuvềvịtrívàvậntốc
m
F
r
e
e
x
r
O
DepartmentofAppliedMechanics 8
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
2.Cácbàitoáncơbảncủađộnglựchọcchấtđiểm
Bài toán 1. [Bt thuận]. Cho biết các lực tác dụng lên chất điểm và các điều kiện đầu của chuyển động (vị trí và
vận tốc ban đầu), xác định chuyển động của chất điểm ấy.
Bài toán 2. [Bt ngược]. Cho biết chuyển động của chất điểm, xác định lực tác dụng lên chấtđiểm.
Bài toán 3. [Bt hỗn hợp]. Cho biết một số lực tác dụng (lực hoạt động) và một số thông tin về chuyển động
(như quĩ đạo, vị trí và vận tốc ban đầu), xác định chuyển động của chất điểm và các lực chưa biết (lực liên kết).
ma F r v t(, ,)

Nếuchấtđiểmchịutácdụngcủanhiềulực
ac
kj
FF F=å +å

Quanhệlựcvàgiatốc(chuyểnđộng)như sau
k
FF=å

Đốivớichấtđiểmchịuliênkết
m
F
F1
F2
O
g
a
F
c
F
F
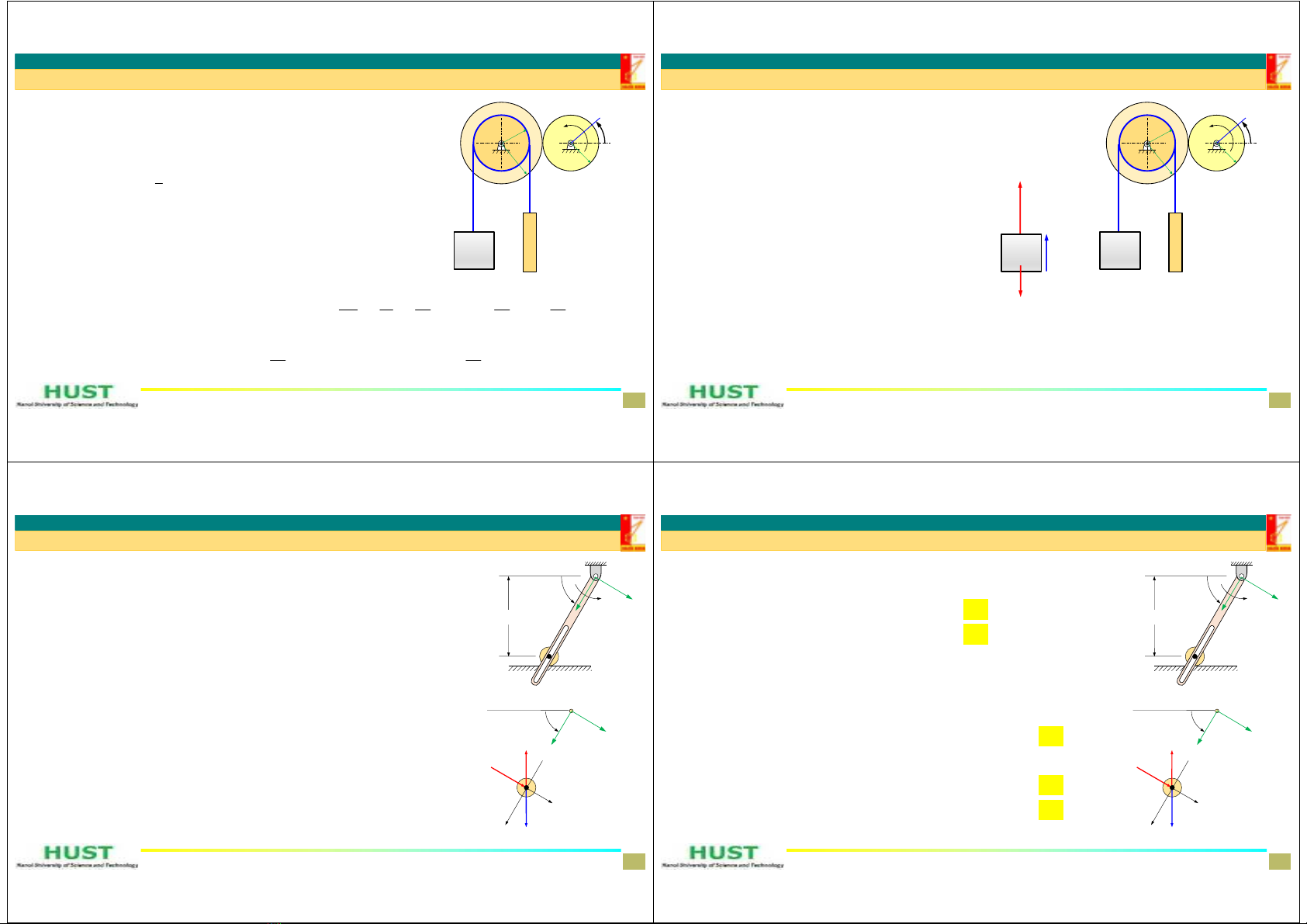
DepartmentofAppliedMechanics 9
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
3.Cácvídụápdụng/vídụ1
Ví dụ 1. Mô hình thang máy như trên hình. Động cơ nối vào bánh răng
1(r
1,z
1), truyền động sang bánh răng 2 (r2,z
2). Tang cuốn bán kính r
gắn liền bánh răng 2. Dây cuốn không dãn. Trong giai đoạn mở máy,
bánh răng 1 quay nhanh dần đều
2
1
10 0
2,consttqa a==
21
r1
A
r
r2
B
1
m
XácđịnhlựccăngcáptreocabinA,biếtkhốilượngcabinlàm.
Lờigiải
Phântíchchuyểnđộng:
rz z z
tt
rz z z
12 2 1 1
11 0 2 1 0
21 1 2 2
,w
wqa w w a
w
== == = =
AAA
zz
vr r tavr r
zz
11
20 20
22
wa wa== ===
Tínhgiatốccabin
DepartmentofAppliedMechanics 10
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
3.Cácvídụápdụng/vídụ1
ma P T
ma T P
TPmaP ag(1 / )



Am
P
T
a
21
r1
A
r
r2
B
1
m
Táchcabinvàviếtquanhệlực‐ giatốcchocabin
Nếugiatốcahướngxuống
TPmaP ag(1 / )

DepartmentofAppliedMechanics 11
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
3.Cácvídụápdụng/vídụ2
Ví dụ 2. Trụ nhỏ C khối lượng 2‐kg có chốt P đi qua tâm chuyển động trong
rãnh của tay quay OA. Biết rằng tay quay OA chuyển động trong mặt đứng
với vận tốc góc = 0.5 rad/s, hãy xác định lực tác dụng lên trục C (coi như
chất điểm) tại thời điểm =60.
h=0.4m
O
CP
A
r
e
e
Lời giải
Vị trí của C được xác định bởi khoảng cách OC và góc ,dođótasử
dụng tọa độ cực để giải bài toán này.
Sơ đồ giải phóng liên kết
Cáclựctácdụnglêntrụbaogồm:trọnglựcW,phảnlựccủanềnNC,vàlực
FPdo rãnh của OA tác dụng vuông góc OA, chiều được giả sử trước.
Chiều của các thành phần gia tốc arvà aθđược chọn như trên hình.
Ởđâycóbốnẩncầntìmlàar,aθ,FPvà NC.W
NC
Fp
a
ar
r
e
e
O
DepartmentofAppliedMechanics 12
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
3.Cácvídụápdụng/vídụ2
Phươngtrìnhquanhệlực–giatốc
Từhìnhvẽtaviếtđượccácphươngtrình
Cr
PC
WN a
WFN a
sin sin 2
cos cos 2




h=0.4m
O
CP
A
r
e
e
W
NC
Fp
a
ar
r
e
e
O
Wmg 19.62 N29.81
Động học
r
arr ar r
2,2




Từhìnhvẽtaxácđịnhđượcliênhệgiữarvàθ
Đạohàmhailầnphươngtrìnhliênkếttanhậnđược
rhsin 0

2
sin cos 0,
sin 2 cos cos sin 0
rr
rr r r






(1)
(2)
(4)
(5)
(3)
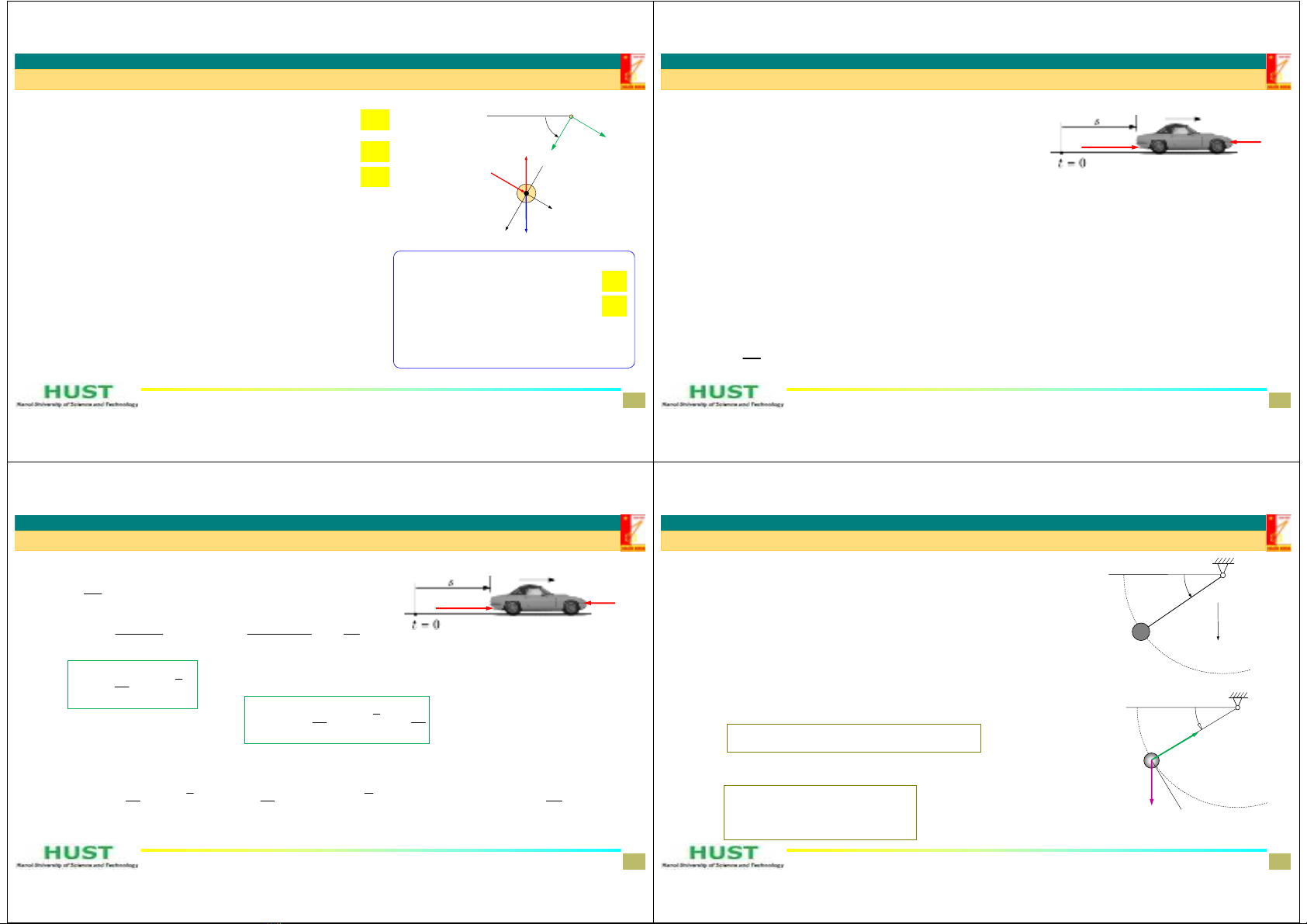
DepartmentofAppliedMechanics 13
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
3.Cácvídụápdụng/vídụ2
Từhệ(1)và(2)vớiθ=60chota
NC=19.4N,FP=‐0.356N.
DấutrừchứngtỏrằngFPtácđộngngượcchiềuhìnhvẽ.
0.462,
0.133, 0.192rrr 
22
0.192 0.462(0.5) 0.0770
r
arr


0 2( 0.133)(0.5) 02.133ar r

 

rhsin 0

2
sin cos 0,
sin 2 cos cos sin 0
rr
rr r r






Giảihệbaphươngtrình
với tanhậnđược:
60 , 0.5, 0



Tínhđược:
(4)
(5)
(3)
W
NC
Fp
a
ar
r
e
e
O
Cr
PC
WN a
WFN a
sin sin 2
cos cos 2




Wmg 19.62 N29.81
(1)
(2)
DepartmentofAppliedMechanics 14
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
3.Cácvídụápdụng/vídụ3
Lực cản tỷ lệ vận tốc
Ví dụ 3.Xeôtôchuyểnđộngtrênđườngthẳngngangtừ
trạngtháiđứngyêndolựcđẩyP=const,lựccảntỷlệvận
tốcxe.
•Tìmbiểuthứcvậntốccủaxelàhàmtheothờigian.
•TìmkhoảngthờigianTcầnthiếtđểchovậntốcđạtgiátrị
bằng95%giátrịvậntốcgiớihạn.
c
Fkv
m
P
Lờigiải
Phântíchchuyểnđộng:XechuyểnđộngngangdướitácdụngcủahailựcPvàFc.
x
mx F x v t mv P kv(,,) ,

Cầnđigiảiphươngtrình viphânbậcnhấtvớiđiềukiệnđầu
dv
mPkv v
dt ,(0)0

DepartmentofAppliedMechanics 15
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
3.Cácvídụápdụng/vídụ3
k
mt
P
vt e
k
() (1 )

mdv d P kv k
dt dt
Pkv Pkv m
[]
[]


c
Fkv
m
P
dv
mPkv v
dt ,(0)0
kkS
mm
TT
PP m
vT e e T
kk k
() (1 ) 0.95 0.05 ln20


•Tìm biểu thức vận tốc của xe là hàm theo thời gian
•Tìm khoảng thời gian T cần thiết để cho vận tốc đạt giá trị bằng 95% giá trị vận tốc giới hạn.
•Tìm vận tốc tới hạn của xe
k
mt
gh t
PP
ve
kk
lim (1 )


DepartmentofAppliedMechanics 16
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
3.Cácvídụápdụng/vídụ4
tn
al a l
2
,,


2
cos
sin
t
n
ma ml P
ma ml T P




m
l
O
g
Vídụ4.Chấtđiểmchịuliênkết(sửdụngtọađộtựnhiên)
Một quả cầu nhỏ khối lượng m được treo vào một dây mềm không
dãn luôn căng chiều dài L đầu kia cố định. Quả cầu được thả từ vị trí
dây ngang không vận tốc ban đầu. Tìm vận tốc của quả cầu phụ thuộc
vị trí của nó và lực căng dây (dây luôn căng).
O
P
T
m
n
Lờigiải
PT,
Phântíchchuyểnđộng:điểmchuyểnđộngtrênđườngtrònđãbiết.Sử
dụngphươngpháptọađộtựnhiên.Cáclựctácdụng
nt
ma P T m a a P T() 



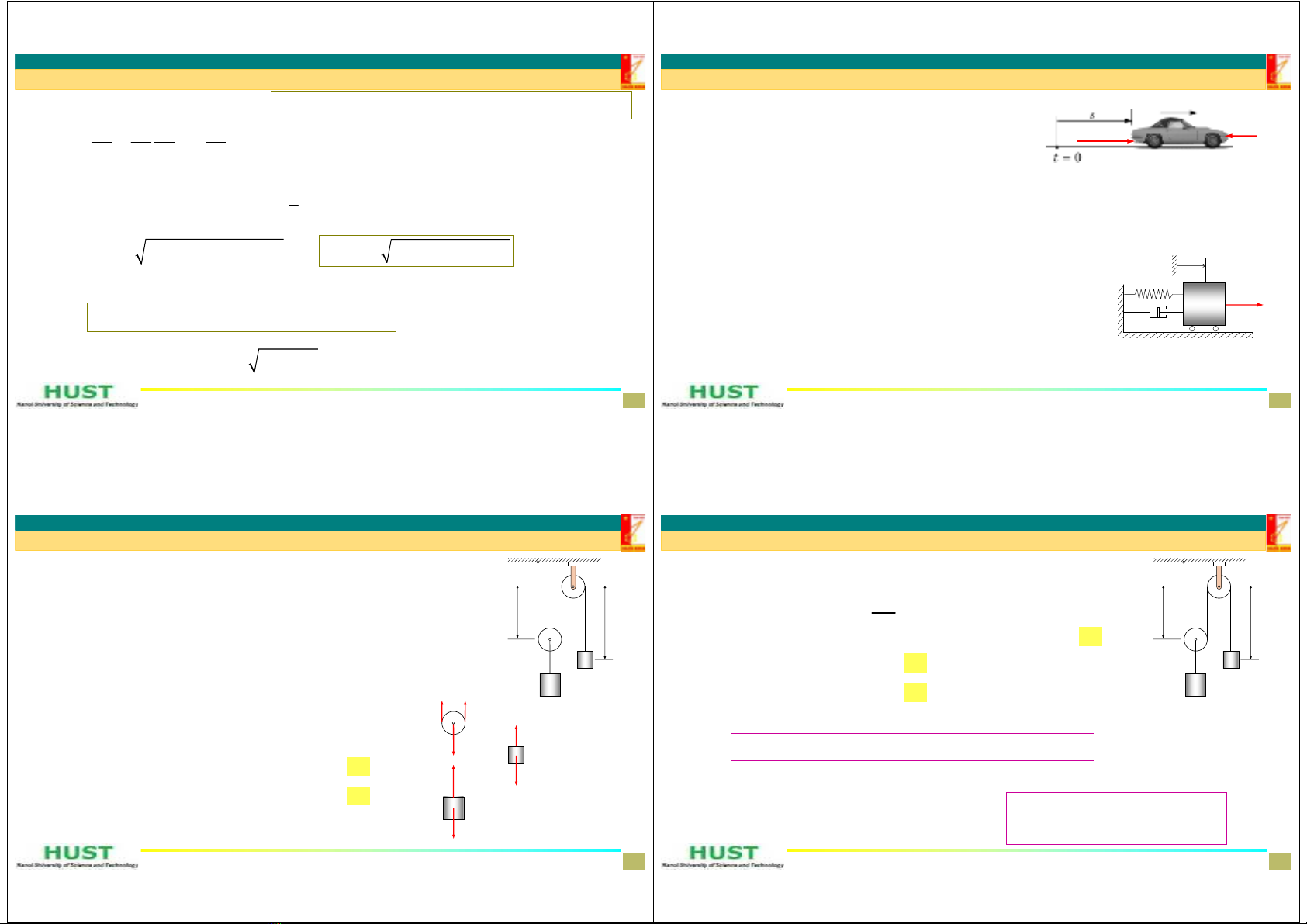
DepartmentofAppliedMechanics 17
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
3.Cácvídụápdụng/vídụ4
Lựccăngdây:
0
2
0
0
1
cos (sin sin )
2
ml d P d ml mg





1
0
2(sin sin)gl


0
2(sin sin )vl gl


2
0
sin (3sin 2sin )Tml P mg


If v gl T mg (0)=0 2 sin , 3 sin


ddd d
dt d dt d




 cos cosml P ml d P d



Sửdụnghệthức
Dựavàocácđiềukiệnđầucủachuyểnđộng,tacó:
tn
ma ml P ma ml T P
2
cos , sin



Vậntốcchấtđiểm:
DepartmentofAppliedMechanics 18
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
3.Cácvídụápdụng/vídụ5
Mộtsốdạngphươngtrình viphânchuyểnđộngcầngiải
mv P kv v,(0)0

mv P kv v
2,(0)0
mx cx kx F t x x x v
000
sin , (0) , (0)

mx kx F t x x x v
000
sin , (0) , (0)

mx kx x x x v
00
, (0) , (0)

mx cx kx x x x v
00
,(0),(0)

n
c
Fkv
m
P
x
k
m
c
F(t)
mx P x x x v
00
, (0) , (0)

(1)
(2)
(3)
(4)
(5)
(6)
(7)
DepartmentofAppliedMechanics 19
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
3.Cácvídụápdụng/vídụ6
A
C
O
B
D
sAsB
Vídụ6.Hệchấtđiểmchịuliênkết(bỏquakhốilượngpuli).
Vật nặng A khối lượng 100 kg được thả từ trạng thái đứng yên. Nếu bỏ qua khối
lượng các puli và dây, hãy xác định vận tốc của vật nặng B khối lượng 20 kg sau
thời gian 2 giây.
WA
WB
2T
2T
TT
T
Lờigiải
Sơđồgiảiphóngliênkết
Dobỏquakhốilượngcácpuli,nênlựccănglàkhôngđổitrongmỗidây.
GọilựccăngtrongnhánhdâytreovậtBlàT,từsơđồlựctrênpuliCta
suyralựctreovậtAlà2T.BaẩntrongbàitoánnàylàT,aAvàaB.
: 981 2
AA
ma T
:209.81
BB
ma T
VậtA:
VậtB:
Cácphươngtrìnhlực‐giatốc
(1)
(2)
DepartmentofAppliedMechanics 20
Độnglựchọccơ hệ:Lực– giatốc.Kineticsofamechanicalsystems:Force‐ acceleration
AB
d
sslconstdt
2
2
2 (..)
 AB
AB
ss
aa
20
20


 
AB
Ta a
22
327.0 N, 3.27 m/ s , 6.54 m/ s
0
0 ( 6.54)(2) 13.1m/ s
B
vv at

3.Cácvídụápdụng/vídụ6
Độnghọc
Từđiềukiệndâykhôngdãntacóđượcliênhệ(dâyO‐>BdàiL)
NhưvậyvậtAcógiatốchướngxuống,vậtBcógiatốchướnglên.
AA
ma T981 2
BB
ma T20 9.81
Giảihệbaphươngtrìnhtrêntanhậnđược
(3)
(1)
(2)
Cácphươngtrìnhlực‐giatốc
VậttốcvậtBsau2giâyđượcxácđịnhnhưsau:
DấutrừchứngtỏvậtBcóvậntốchướnglên.
A
C
O
B
D
sAsB