intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Cơ lưu chất: Chương 2 - PGS.TS.Nguyễn Thị Bảy

Chia sẻ: Luong My | Ngày: | Loại File: PDF | Số trang:26

Thêm vào BST
Báo xấu
765
lượt xem 143
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Chương 2 Tĩnh học lưu chất thuộc bài giảng cơ lưu chất, có kết cấu nội dung được phân làm 9 mục, trình bày kiến thức lý thuyết, các công thức và bài tập ví dụ về tĩnh học lưu chất. Mời các bạn cùng tham khảo và học tốt.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Cơ lưu chất: Chương 2 - PGS.TS.Nguyễn Thị Bảy

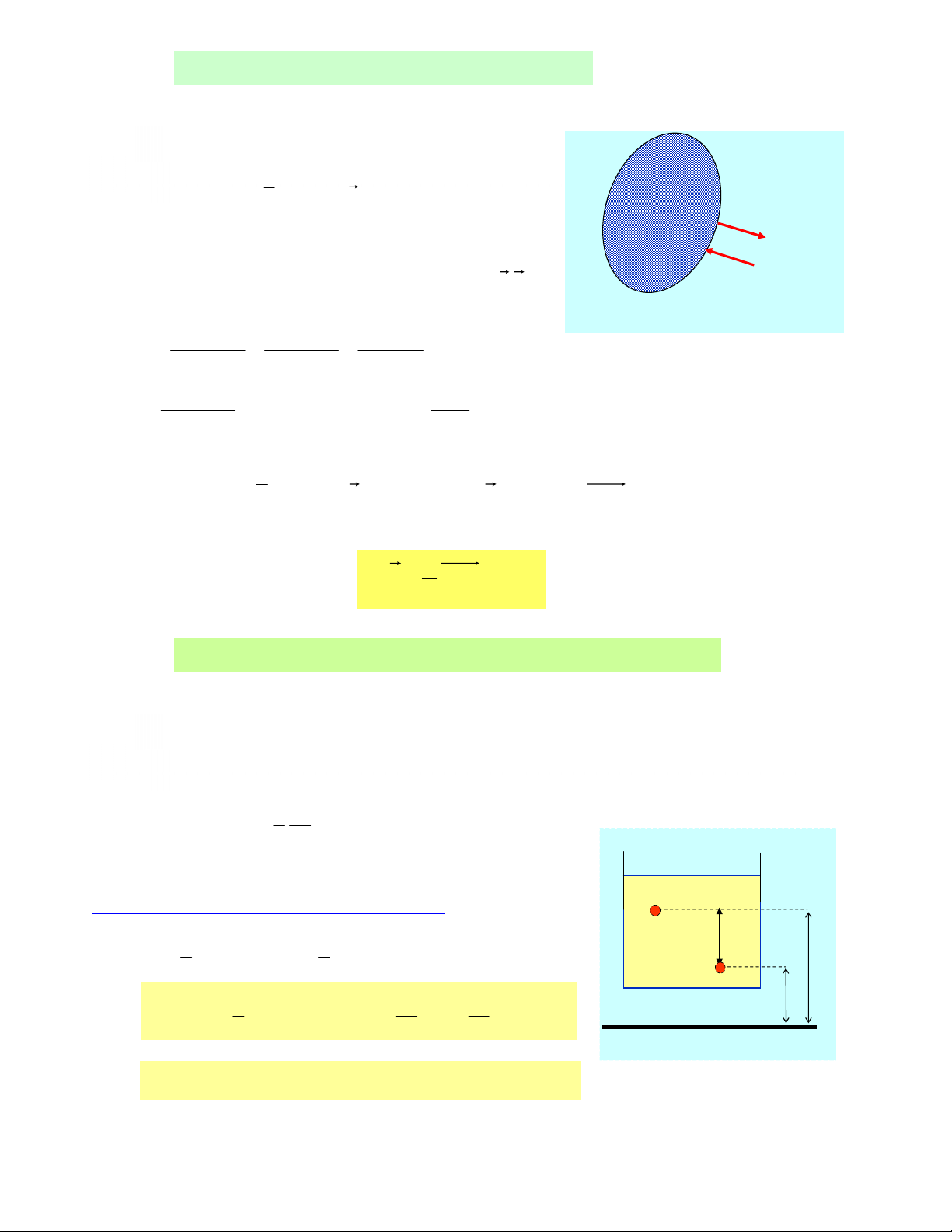
  1. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay CHÖÔNG I. HAI TÍNH CHAÁT CUÛA AÙP SUAÁT THUYÛ TÓNH 1. p ⊥ A vaø höôùng vaøo A. (suy ra töø ñònh nghóa). 2. Giaù trò p taïi moät ñieåm khoâng phuï thuoäc vaøo höôùng ñaët cuûa beà maët taùc duïng. Xem phaàn töû löu chaát nhö moät töù dieän vuoâng goùc ñaët taïi goác toaï ñoä nhö hình veõ: Caùc löïc leân phaàn töû löu chaát: Löïc maët : pxδyδz; pyδxδz; pzδyδx; pnδyδs. Löïc khoái: ½Fδxδyδzρ. z Toång caùc löïc treân phöông x phaûi baèng khoâng: pn n pxδyδz - pnδyδs(δz/δs) + ½Fxδxδyδzρ = 0 δz y Chia taát caû cho δyδz : px δx θ δs x px - pn + ½Fxρδx = 0 ⇒ px = pn khi δx → 0. δy Chöùng minh töông töï cho caùc phöông khaùc pz Suy ra: px =py = pz = pn THUY TINH 1
  2. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay II. PHÖÔNG TRÌNH VI PHAÂN CÔ BAÛN Xeùt löu chaát ôû traïng thaùi caân baèng coù theå tích W giôùi haïn bôûi dieän tích A. Ta coù toång caùc löïc taùc duïng leân löu chaát =0: Löïc khoái + löïc maët = 0: W ∫∫∫ Fρdw − ∫∫ pdA = 0 w A A n Ta xeùt treân truïc x: b .d .Gauss p ∫∫∫ F ρdw − ∫∫ p dA = 0 ⇔ ∫∫∫ F ρdw − ∫∫∫ div (p.n w x A x w x W x )dw = 0 ⎛ ∂ ( p x n xx ) ∂ ( p y n xy ) ∂ ( p z n xz ⎞ ⇔ ρFx − ⎜ ⎜ ∂x + + ⎟=0 ⎝ ∂y ∂z ⎟ ⎠ ∂ ( p x n xx ) p=p x =p y = p ∂ ( p) ⇔ ρFx − = 0 ←⎯ ⎯ ⎯ z → ρFx − ⎯ =0 ∂x ∂x Xeùt töông töï cho caùc truïc khaùc Keát luaän: ∫∫∫ Fρdw − ∫∫ pdA = 0 ⇔ ∫∫∫ Fρdw − ∫∫∫ grad (p)dw = 0 w A w W 1 ⇔ F− grad ( p ) = 0 ρ III. TÍCH PHAÂN PHÖÔNG TRÌNH VI PHAÂN CÔ BAÛN ⎧ 1 ∂p ⎫ ⎪Fx − ρ ∂x = 0 × dx ⎪ ⎪ ⎪ ⎪ 1 ∂p ⎪ 1 ⎨Fy − = 0 × dy ⎬+ ⇒ (Fx dx + Fy dy + Fz dz) − dp = 0 ⎪ ρ ∂y ⎪ ρ ⎪ 1 ∂p ⎪ ⎪Fz − = 0 × dz ⎪ ⎩ ρ ∂z ⎭ pa Chaát loûng naèm trong tröôøng troïng löïc: Fx, Fy=0, Fz=-g: pA 1 ρ=const p hAB − gdz= dp⎯⎯⎯ gz+ = const → zA ρ ρ pB p p p zB hay: z + = const ⇔ zA + A = zB + B (1) chuaån 0 γ γ γ hay: pB = pA + γhAB hay p = pa+γh (2) (1), (2) laø phöông trình thuyû tónh THUY TINH 2
  3. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay Chaát khí naèm trong tröôøng troïng löïc, neùn ñöôïc: pV p Xem nhö chaát khí laø khí lyù töôûng: =R hay = RT T ρ 1 RT − gdz = dp ⇔ −gdz = dp ρ p Neáu bieát ñöôïc haøm phaân boá nhieät ñoä theo ñoä cao, ví duï: T=T0 – az; a>0, T0 laø nhieät ñoä öùng vôùi ñoä cao z=0 (thoâng thöôøng laø möïc nöôùc bieån yeân laëng): R(T0 − az) dp dz g − gdz = dp ⇒ = −g ⇒ ln p = ln(T0 − az) + ln(C) p p R(T0 − az) aR g ⇒ p = C(T0 − az) aR g p0 Goïi p0 laø aùp suaát öùng vôùi z=0: p 0 = CT0 aR ⇒ C = g T0 aR g ⎛ T − az ⎞ aR Phöông trình khí tónh: p = p0 ⎜ 0 ⎟ ⎜ T ⎟ ⎝ 0 ⎠ AÙp suaát tuyeät ñoái taïi maët bieån yeân laëng laø 760mmHg, töông öùng vôùi Ví duï 1: nhieät ñoä T=288 0K. Nhieät ñoä taàng khí quyeån giaûm 6,5 ñoä K khi leân cao 1000m cho ñeán luùc nhieät ñoä ñaït 216,5 ñoä K thì giöõ khoâng ñoåi. Xaùc ñònh aùp suaát vaø khoái löôïng rieâng cuûa khoâng khí ôû ñoä cao 14500m. Cho R=287 J/kg.0K Giaûi: T0 laø nhieät ñoä öùng vôùi ñoä cao z=0 (maët bieån yeân laëng): Ta tìm haøm phaân boá nhieät ñoä theo ñoä cao: T=T0 – az; vôùi a=0, 0065 Cao ñoä öùng vôùi nhieät ñoä T1=216,5 ñoä K laø z1= 11000m Suy ra: 216,5=288 – 0,0065z1 Nhö vaäy töø z0=0 ñeán z1=11000m, aùp suaát bieán thieân theo phöông trình khí tónh: g g 9.81 ⎛ T0 − az ⎞ aR ⎛ T0 − az1 ⎞ aR ⎛ 216,5 − 0.0065 *11000 ⎞ 0.0065*287 p = p0 ⎜ ⎜ T ⎟ ⇒ p1 = p 0 ⎜ T ⎟ ⎜ ⎟ ⎟ = 0.76⎜ ⎟ ⎝ 0 ⎠ ⎝ 0 ⎠ ⎝ 216,5 ⎠ p1 = 0.1695mHg Töø: p p1 0 . 1695 * 13 . 6 * 9 . 81 * 10 3 = RT ⇒ ρ 1 = = = 0.364 kg/m 3 ρ RT 1 287 * 216 . 5 THUY TINH 3
  4. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay Töø z1=11000 m ñeán z2=14500m, nhieät ñoä khoâng ñoåi neân: RT1 RT1 dp RT1 ⎛ − RT1 ⎞ RT − 1 − gdz = dp ⇒ dz = − ⇒z=− ln p + ln(C) = ln⎜ Cp g ⎟ ⇒ Cp g = e z p g p g ⎜ ⎟ ⎝ ⎠ Taïi ñoä cao z1 ta coù aùp suaát baèng p1; suy ra: g e z1 ( z1 − z ) C= RT1 ⇒ p = p1e RT1 (p1 ) g Nhö vaäy taïi ñoä cao z2 =14500m ta tính ñöôïc: g 9.81 ( z1 − z 2 ) (11000−14500 ) p 2 = p1e RT1 = 0.17 * e 278*216.5 = 0.09752 mHg = 97.52mmHg p 2ρ1 vaøø: ρ2 = = 0.209kg / m 3 p1 IV. MAËT ÑAÚNG AÙP, P TUYEÄT ÑOÁI, P DÖ, P CHAÂN KHOÂNG Maët ñaúng aùp cuûa chaát loûng naèm trong tröôøng troïng löïc laø maët phaúng naèm ngang Phöông trình maët ñaúng aùp: Fxdx + Fydy + Fzdz=0 AÙp suaát dö : pdö = ptñ - pa Neáu taïi moät ñieåm coù pdö < 0 thì taïi ñoù coù aùp suaát chaân khoâng pck pck= -pdö = pa – ptñ p trong phöông trình thuyû tónh laø aùp suaát tuyeät ñoái ptñ. hoaëc aùp suaát dö 0 5 6 Các điểm naøo (?) có áp suất bằng nhau; 7 trong ñoaïn oáng 2-5-6 chöùa chaát khí hay 1 2 3 4 chaát loûng ? THUY TINH 4
  5. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay V. ÖÙNG DUÏNG 1. Caùc aùp keá: p=0, chaân khoâng tuyeät ñoái pa B B htñA hdöA pa A B hckA A A pA = pB + γhtd pduA = pduB + γhdu = γhdu pduA = pduB − γhck ⇒ pckA = γhck 2. Ñònh luaät bình thoâng nhau: A’ A’ B’ γ2 h2 Töø p.tr thuyû tónh: pA=pA’+ γ2h2; pB=pB’+ γ1h1 h1 A B Suy ra γ1h1=γ2h2 γ1 3. Ñònh luaät Pascal: f Taïi moät vò trí naøo ñoù trong löu chaát neáp aùp suaát taêng leân moät ñaïi löôïng Δp thì ñaïi löôïng naøy seõ ñöôïc truyeàn ñi trong toaøn mieàn löu chaát p=f/a → öùng duïng trong maùy neùn thuûy löïc. F=pA Pascal 1623-1662 , Phaùp THUY TINH 5
  6. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay 4. Bieåu ñoà phaân boá aùp suaát chieàu saâu: pa pa pa h h h pa+γh pdö=γh pdö/γ=h pck pck pck pck/γ pck pck/γ h h h h1=pck/γ pdö=0, ptñ=pa pck-γh pck/γ-h pdö/γ=h-h1 5 . Phaân boá aùp suaát treân moät maët cong: h p/γ=h p/γ=h 6 . AÙp keá vi sai: pa→pa+ Δp pa Ban ñaàu thì p1=p2=pa: γ1h1= γ2h2 C Δz A γ2 Khi aùp suaát oáng beân traùi taêng leân Δp: p1=pa+Δp; p2=pa γ1 h1 B pa + Δp = pA = p B − γ1h AB = pC + γ 2 h BC − γ1h AB h2 = pa + γ 2 h BC − γ1h AB h 0 ⇒ Δp = γ2hBC − γ1hAB = γ2 (h2 − h + Δz) − γ1(h1 − h − Δz) ⇒ Δp = h ( γ1 − γ 2 ) + Δz( γ1 + γ 2 ) Goïi A, a laàn löôït laø dieän tích ngang oáng lôùn vaø oáng nhoû: ah ah ⇒ a.h = A.Δz ⇒ Δz = ⇒ Δp = h( γ1 − γ 2 ) + ( γ1 + γ 2 ) A A THUY TINH 6
  7. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay VI. LÖÏC TAÙC DUÏNG LEÂN THAØNH PHAÚNG Giaù trò löïc pa O(x) du du = ∫ p dA = α F ∫ γhdA = ∫ γy sin αdA hD h A A A y = γ sin α ∫ ydA =γ sin αy C A = γh C A = p du A C hC A F dA F =p A du du C Ñieåm ñaët löïc C yD D y D F = ∫ ydF = ∫ yγ sin αydA = γ sin α ∫ y 2dA = γ sin αIxx y A A A Taâm aùp Suy ra: γ sin αI xx I I +y A 2 löïc yD = = xx = C C F yCA yCA x IC Ixx=Ic+yC2A yD = yC + y yC yCA Ixy=Ix’y’+xCyCA Töông töï : Ic γ sin αI xy I xy I x 'y ' + x C y C A xD = = = C F yCA yCA Ix ' y ' x D = xC + Ic: M. q tính cuûa A so vôùi truïc //0x vaø qua C ycA Ix’y’: M. q tính cuûa A so vôùi troïng taâm C Löïc taùc duïng leân thaønh phaúng chöõ nhaät ñaùy naèm ngang: hA + hB pC = γ Ω hA 2 F hA A hA + hB hB ⇒ F = ApC = γ (AB)b C* 2 hB D B Ñaët: Ω=(hA+hB).(AB)/2 Suy ra: F=γΩb BD=[(hB+2hA)/(hB+hA)].(AB)/3 THUY TINH 7
  8. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay VII. LÖÏC TAÙC DUÏNG LEÂN THAØNH CONG ÑÔN GIAÛN F = Fx + Fy + Fz2 2 2 Az dAz O(y) pa x Thaønh phaàn löïc theo phöông x Maët Fx = ∫ dFx = ∫ pdA cos(n, ox) h cong A A A Ax = ∫ γhdA x = ∫ γhdA x = p cx A x dFx A Ax dAx (n,ox) Thaønh phaàn löïc theo phöông z n z dA Fz = ∫ dFz = ∫ γhdA cos(n, oz) A A = ∫ γhdA z = γW A W: theå tích vaät aùp löïc: laø theå tích cuûa vaät thaúng ñöùng giôùi haïn bôûi maët cong A vaø hình chieáu thaúng ñöùng cuûa A leân maët thoaùng töï do (Az) pa Caùc ví duï veà vaät aùp löïc W: pdö/γ pa pdö pck Fz pck/γ Fz pa w w w pck pa pck w Fz Fz1 pck/γ pck/γ w1 pa Fz w w2 pa Fz2 Pa Pck Pck Pa Pdu w w Fz Fz Fz w Pa THUY TINH 8
  9. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay pa pa pdö pdö Fz Fz W1: phaàn cheùo lieàn neùt W1: phaàn cheùo lieàn neùt →Fz1 höôùng xuoáng. →Fz1 höôùng leân. W2: phaàn cheùo chaám W2: phaàn cheùo chaám chaám chaám →Fz2 höôùng xuoáng. →Fz2 höôùng leân. W=W1-W2 W=W1-W2 →Fz höôùng xuoáng →Fz höôùng leân Löïc ñaåy Archimeøde: Ar W1 Ar = γW2 − γW1 = γW W W2 (phaàn gaïch cheùo) Archimede 287-212 BC THUY TINH 9
  10. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay VIII. SÖÏ CAÂN BAÈNG CUÛA MOÄT VAÄT TRONG LÖU CHAÁT Ar = −G Ar G Ar Vaät chìm lô löûng D C DC C D G G Ar oån ñònh khoâng oån ñònh Phieám ñònh A G Vaät noåi Ar Ar C M C C M yy D D D G G Ar oån ñònh: MD>CD khoâng oån ñònh:MD
  11. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay Ví duï 3: Bình ñaùy vuoâng caïnh a=2m. Ñoå vaøo bình hai chaát loûng khaùc nhau, δù1 =0,8; δ 2=1,1. V1=6m3; V2=5m3. Tìm pB Giaûi: γ1= δù1 γn=0.8*9.81*10^3 N/m3 pa γ2 γ2= δù2 γn=1.1*9.81*10^3 N/m3 γ1 h1 A h2 B Goïi h2 laø beà daøy cuûa lôùp chaát loûng 2: h2=(5/4)m. h=1m Goïi h1 laø beà daøy cuûa lôùp chaát loûng 1: h1=(6/4)m. a=2m Ta coù hAB = h2 – h = 0.25m Suy ra: pB=pA+γ2*hAB= pA + γ2*(0.25) Suy ra: pB= pa+ γ1*h1 + γ2*(0.25) Suy ra: pdu B= 0+ γ1*(1.5) + γ2*(0.25)=9.81*103(0.8*1.5+1.1*0.25)=14.5 m nöôùc Thí nghiệm: Ottovon Guericke (8.5.1654) tại Maydeburg, Đức Dùng 2 bán cầu D = 37 cm, bịt kín và hút khí để áp suất tuyệt đối trong qủa cầu bằng không . Cho 2 đàn ngựa kéo vẫn không tách bán cầu ra được. Vậy phải cần 1 lực bằng bao nhiêu để tách hai bán cầu ra (xem lực dình giữa 2 bán cầu không đáng kể) Chân không p(tuyệt đối) = 0 D F =? F =? THUY TINH 11
  12. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay Van phaúng AB hình chöõ nhaät cao 1,5m, roäng 2m, quay quanh truïc A Ví duï 4: naèm ngang nhö hình veõ. Tính aùp löïc nöôùc taùc duïng leân van . Tính löïc F (xem hình veõ) ñeå giöõ van ñöùng yeân Giaûi: Giaù trò löïc: Fn du = p du A = γh C A = 9.81*103 * (5 − 1,5 / 2) *1,5 * 2 C = 125.0775 KN Vò trí ñieåm ñaët löïc D: pa 2 *1.53 O I 12 y D = y C + C = 4.25 + = 4.294m yC=hC yCA 4.25 *1.5 * 2 A yD ⇒ DB = 5 − 4.294m = 0.706m 5m 1,5m C Tính caùch khaùc: Fn D C* F? h + 2h A AB 5 + 2 * 3.5 1.5 B DB = B . = = 0.706m hB + hA 3 5 + 3.5 3 y Ñeå tính löïc F giöõ van yeân, ta caân baèng moment: Fn(AD)=F(AB) Suy ra: F=Fn(AD)/(AB)=125.07*(1.5-0.706)/(1.5) = 66.22 KN Ví duï 5: Van phaúng ABE hình tam giaùc ñeàu coù theå quay quanh truïc A naèm ngang nhö hình veõ. Tính aùp löïc nöôùc taùc duïng leân van vaø vò trí ñieåm ñaëc löïc D . Tính löïc F ngang (xem hình veõ) ñeå giöõ van ñöùng yeân Giaûi: pa O hC = 3+2/3 = 3.666m E AB chính laø chieàu cao cuûa tam giaùc ñeàu, 3m A 2 2 4 hC AB = = = = 2.31m A 0 sin(60 ) 3 3 C 2 Caïnh ñaùy AE cuûa tam giaùc: AE=2*AB/tg(600)=2.667m 2m C D Fn B Dieän tích A cuûa tam giaùc: A=(AE)*(AB)/2=3.079 m2 α=600 F B AÙp löïc: Fndu =γhCA=9.81*3.666*3.079 = 110,76 KN Toaï ñoä yC = OC= hC/sin(600) = 4.234m y 3 3 b*h 2.667 * 2.31 I OD = y D = y C + C = y C + 36 = 4.234 + 36 = 4.304m yCA yCA 4.234 * 3.079 Fn(AD)=F(2) Suy ra: F=Fn(AD)/(2)=110.76*(OD-OA)/2 = 110.76*(4.304-3.464)/2 =46.507 KN THUY TINH 12
  13. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay Ví duï 6: Van phaúng ABE hình tam giaùc ñeàu coù theå quay quanh truïc A naèm ngang nhö hình veõ. Tính aùp löïc nöôùc taùc duïng leân van vaø vò trí ñieåm ñaëc löïc D . Tính löïc F ngang (xem hình veõ) ñeå giöõ van ñöùng yeân Giaûi: pa O hC = 1+ 3+2/3 = 4.666m 1m P0du = 0,1at AB chính laø chieàu cao cuûa tam giaùc ñeàu, 2 2 4 E AB = 0 = = = 2.31m sin(60 ) 3 3 3m hC A 2 A C Caïnh ñaùy AE cuûa tam giaùc: AE=2*AB/tg(600)=2.667m Dieän tích A cuûa tam giaùc: A=(AE)*(AB)/2=3.079 m2 C 2m D AÙp löïc: Fndu =γhCA=9.81*4.666*3.079 = 140,97 KN Fn B α=600 F Toaï ñoä yC = OC= hC/sin(600) = 5.389m B b * h3 2.667 * 2.313 I y OD = y D = y C + C = y C + 36 = 5.389 + 36 = 5.444m yCA yCA 5.389 * 3.079 Fn(AD)=F(2) Ghi chuù: OA=4/sin(600) Suy ra: F=Fn(AD)/(2)=140.97*(OD-OA)/2 = 140.97*(5.444 – 4.619)/2 =58.133 KN Van phaúng ABE hình tam giaùc ñeàu coù theå quay quanh truïc A naèm Ví duï 7: ngang nhö hình veõ. Tính aùp löïc nöôùc taùc duïng leân van vaø vò trí ñieåm ñaëc löïc D . Tính löïc F ngang (xem hình veõ) ñeå giöõ van ñöùng yeân Giaûi: pC = -γhC = -9.81*103*(1+ 2-2/3) = -9.81*103* 2.333 N/m2 P0ck = 0,6at AB =2.31 m AE= 2.667m 3m A A=3.079 m2 A C AÙp löïc: Fndu =-γhCA=-9.81*2.333*3.079 D = -70.483 KN 2m C Fn B hC α=600 F Toaï ñoä yC = - OC= hC/sin(600) = -2.694 m B 1m pa O b*h 3 2.667 * 2.31 3 y I OD = y D = y C + C = y C + 36 = −2.694 + 36 = -2.804m yCA yCA − 2.694 * 3.079 Fn(AD)=F(2) Ghi chuù: OA=3/sin(600) Suy ra: F=Fn(AD)/(2)=140.97*(OA-OD)/2 = 70.483*(3.464 – 2.804)/2 =23.25 KN THUY TINH 13
  14. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay Ví duï 8: Van tam giaùc ñeàu ABM caïnh AB=1m ñaët giöõ nöôùc nhö hình veõ (caïnh AB thaúng ñöùng). Aùp suaát treân bình chöùa laø aùp suaát khí trôøi. Bieát hA=1m. Goïi D laø vò trí ñieåm ñaët löïc F cuûa nöôùc taùc duïng leân van öùng vôùi ñoä saâu laø hD. Xác định hD pa ĐS: hD=1,53m Hdẫn: Ta để ý thấy công thức tính moment quán tính hA A A đối với tam giác như trong phụ lục: hD bh 3 M Ic = (*) D 36 so với trục song song với một trong 3 cạnh (đáy b) B B Trong khi đó, từ lý thuyết đã chứng minh, để xác định vị trí D ta áp dụng công thức: IC y D = yC + yC A Với Ic là moment q tính của diện tích A so với trục song song Ox và qua trọng tâm C của A Như vây, muốn ứng dụng công thức (*) trong tính toán yD cần phải có một trong 3 cạnh của tam giác phải song song với Ox (cụ thể là nằm ngang). Trong hình vẽ của bài toán, không có cạnh nào của tam giác nằm ngang, nên trước tiên cần chia tam giác ra hai sao cho một cạnh của mỗi tam giác nhỏ nằm ngang. Sau đó tính lực và vị trí điểm đặt lực riêng đối với từng tam giác nhỏ. Cuối cùng tìm vị trí điểm đặt lực tổng theo công thức: F1 yD1 + F2 yD2 yD = F1 + F2 Ví duï 9: Một hệ thống tự động lấy Cửa có bề nước vào ống đường kính D = 0,3 m rộng b được thiết kế bằng một cửa chắn chữ Cửa chắn nước L. Cửa chắn có bề rộng (thẳng góc với vuông góc trang giấy) b = 1,2m và quay quanh O. Nước Biết áp suất trong ống là áp suất khí Trục quay trời và trọng lượng cửa không đáng kể. a) Giải thích cơ chế hoạt động của cửa D khi độ sâu h thay đổi. b) Xác định độ sâu h tối thiểu để cửa L=1m bắt đầu quay. ống lấy nước HD: Chọn chiều quay ngược chiều kim đồng hồ là chiều dương Phân tích các lực tác dụng lên cửa gồm hai lực: Fx tác động lên phần van chữ nhật thẳng đứng, moment so với O sẽ là: Fxh/3 Fz tác động lên phần diện tích tròn đường kính D, moment so với O sẽ là: FzL Để van có thể lấy nước vào ống thì tổng moment: Fxh/3-FzL = γh3b/6 - γ LhπD2/4 >0 Suy ra: h(γh2b/6 - γ LπD2/4) > 0 suy ra: γh2b/6 > γ LπD2/4 suy ra: h2 > (LπD2/4) / (b/6 ) Suy ra: 3Lπ D2 h> = 0,56m 2b THUY TINH 14
  15. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay Ví duï 10: Moät cöûa van cung coù daïng ¼ hình truï baùn kính R=1,5m; daøi L=3m quay quanh truïc naèm ngang qua O. Van coù khoái löôïng 6000 kg vaø troïng taâm ñaët taïi G nhö hình veõ. Tính aùp löïc nöôùc taùc duïng leân van vaø vò trí ñieåm ñaëc löïc D . Xaùc ñònh moment caàn môû van Giaûi: 1 .5 Fx = p cx A x = γh cx A = 9.81 *10 3 * *1.5 * 3 = 33.10 KN 2 πR 2 π *1 .5 2 Fz = γW = γ L = 9.81 *10 3 * * 3 = 52 KN 4 4 pa O F = Fx2 + Fz2 = 33.10 2 + 52 2 = 61.65 KN 0,6m tg (α ) = Fz = 52 = 1.570796 ⇒ α = 57 ,52 0 0,6mG Fx 1,5m D Fx 33 .1 α M = G * 0.6 = 9.81 * 6000 * 0.6 = 35316 Nm G Fz F nöôùc Ví duï 11: Moät hình truï baùn kính R=2m; daøi L=2m ÔÛ vò trí caân baèng nhö hình veõ . Xaùc ñònh troïng löôïng cuûa phao vaø phaûn löïc taïi A Giaûi: Fz1=γW1 pa R A = Fx = p cx A x = γh cx A x R 2 A = 9.81 *10 3 * * 2 * 2 2 = 39.24 KN nöôùc Fz2=γW2 G + Fz1 + Fz 2 = 0 3 ⇒ G = γW2 - γW1 = 9.81 * L * ( πR 2 + R 2 ) 4 G = 263.3941KN THUY TINH 15
  16. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay Ví duï 12: Moät cöûa van cung coù daïng ¼ hình truï baùn kính R=1,5m; daøi L=2m quay quanh truïc naèm ngang qua O nhö hình veõ. Tính aùp löïc nöôùc taùc duïng leân van vaø vò trí ñieåm ñaëc löïc D . Giaûi: AB = 2R 2 = 2 * 1 .5 2 = 2.12m Fz1 A pa Fx = p cx A x = γh cx A 2 .12 nöôùc = 9.81 * 10 3 * * 2.12 * 2 R 2 450 C O = 44.145 KN 450 Fx ⎛ πR 2 R 2 ⎞ Fz2 Fz = γW = γ ⎜ ⎜ 4 − 2 ⎟L ⎟ α ⎝ ⎠ ⎛ π * 1 .5 2 1 .5 2 ⎞ B F = 9.81 *10 3 * ⎜ ⎜ 4 − ⎟*2 ⎝ 2 ⎟ ⎠ Fz = 12.5989 KN F = Fx2 + Fz2 = 44.145 2 + 12 .60 2 = 45.91 KN Fz 12 .6 tg ( α ) = = = 0.285 ⇒ α = 15 .92 0 Fx 44 .15 Ví duï 13 Moät oáng troøn baùn kính r = 1 m chöùa nöôùc ñeán nöûa oáng nhö hình veõ. Treân maët thoùang khí coù aùp suaát dö po = 0,5 m nöôùc. Bieát nöôùc ôû traïng thaùi tónh. Tính toång aùùp löïc cuûa nöôùc taùc duïng leân ¼ maët cong (BC) treân 1m daøi cuûa oáng po r Giaûi: B C r Fx = p cx A x = γ(0,5 + )r.1 = 9810 * (0,5 + 0,5) *1 = 9810 N 2 r2 Fz = γW = γ ( π + 0,5r ).1 = 9810 *1.285 = 12605.85 N 4 2 F = Fx2 + Fz = 15973.2 N THUY TINH 16
  17. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay Ví duï 14: Moät khoái hình hoäp caïnh a=0,3m ñoàng chaát tyû troïng 0,6 noåi treân nöôùc nhö hình veõ. Tính chieàu saâu ngaäp nöôùc x cuûa hình hoäp . Giaûi: G = Ar ⇔ 0.6*γn*a3 = γn*a2*x x ⇒x= 0.6*a =0.6*0.3 x = 0.18 m Câu 13: Ví duï 15: a a Một vật hình trụ đồng chất có tiết diện hình vuông, cạnh là a = 1m, chiều cao là H = 0,8m. Khi cho vào nước, mực nước ngập H h đến độ cao là h=0,6m. Lực tác dụng lên một mặt bên của vật và tỷ trọng của vật là: Hình câu 14 ĐS: F=1765,8 N; δ=0,75 Ví duï 16: Một quả bóng có trọng lượng 0,02 N, phía dưới có buột một vật nhỏ (bỏ qua thể tích) trọng lượng 0,3N. Cho γkhong khi=1,23 kg/m3. Nếu bơm bóng đầy bằng khí có γkhi=0,8 kg/m3 thì đường kính D quả bóng phải bằng bao nhiêu để bóng có thể bay lên được Gb Gv gamakk gamak Wb D3 D ĐS: 0.02 0.3 1.23 0.8 0.076 0.14 0.52522 Hdẫn: Gb + GVat + Gkhi = γ khongkhiWb → Gb + GVat + γ khiWb = γ khongkhiWb Gb + GVat Wb = γ khongkhi − γ khi Ví duï 17: Vật đồng chất nằm cân bằng lơ lửng trong môi trường dầu-nước như hình vẽ. Biết tỷ trọng của dầu là 0,8. Phần thể tích vật chìm trong nước bằng phần thể tích vật trong dầu. Tỷ trọng của vật ? ĐS: 0,90 Dầu Hướng dẫn: Trọng lượng của vật cân bằng với với lực Vật đẩy Archimede do dầu tác dụng lên nửa cầu trên và nước lên nửa cầu dưới Nước THUY TINH 17
  18. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay Ví duï 18 Moät oáng ño tæ troïng nhö hình veõ coù khoái löôïng M = 0,045kg vaø tieát dieän ngang cuûa oáng laø ω = 290mm2 . Khi boû vaøo trong nöôùc coù tæ troïng δN = 1 , oáng chìm ñeán vaïch A, vaø khi boû vaøo trong daàu coù tæ troïng δD = 0,9 oáng chìm ñeán vaïch B. Tìm khoûang caùch ñoïan AB Giaûi: B • A B • • G = gM = γ n W = γ d ( W + L ABω) ω A Nöôùc • ω Daàu G G ⎛1 ⎞ ⇒ W = ; L AB = ⎜ − 1⎟ γn ωγ n ⎜ δ d ⎟ ⎝ ⎠ 9.81 * 0.045 ⎛ 1 ⎞ L AB = −6 ⎜ − 1⎟ *1000 = 17.24mm 290 *10 * 9810 ⎝ 0.9 ⎠ Ví duï 19: Bình truï troøn chöùa chaát loûng trong ñoù coù thaû phao hình caàu. Bình naøy laïi ñöôïc nhuùng noåi treân maët thoaùng beå chöùa cuøng loaïi chaát loûng. Bieát : Troïng löôïng cuûa bình laø G1; Troïng löôïng cuûa chaát loûng chöùa trong bình laø G2; TyÛ soá caùc chieàu saâu (nhö hình veõ) k=z1/z2; Tìm troïng löôïng cuûa phao Giaûi: Theo ñònh luaät Ar.; toaøn boä heä chòu taùc duïng cuûa G1 löïc ñaåy Ar, höôùng leân, baèng troïng löôïng cuûa khoái chaát loûng bò vaät chieám choã. G Trong khi ñoù löïc theo phöông thaúng ñöùng taùc z1 duïng leân toaøn boä heä bao goàm G+G1+G2 . G2 z2 Vaäy: G + G1 + G2 = Ar = z1A γ vôùi A laø tieát dieän ngang cuûa bình. Ar Xeùt rieâng heä goàm chaát loûng trong bình vaø phao, ta coù troïng löôïng cuûa phao cuõng baèng troïïng löôïng cuûa khoái chaát loûng bò phao chieám trong bình : G = z2A γ -G2 ⇒ Aγ = (G+G2)/z2 G1 Suy ra: G + G1 + G2 = z1(G+G2)/z2 = kG+kG2. ⇒G= − G2 k −1 THUY TINH 18
  19. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay Ví duï 20: Một bình baèng saét hình noùn cuït khoâng ñaùy ( δ=7.8) được uùp như hình vẽ. Đaùy lôùn R=1m, ñaùy nhoû r=0,5m, cao H=4m, daøy b=3mm. Tính giới hạn möïc nöôùc x trong bình ñeå bình khoûi bò nhaác leân. Giaûi: Vnoncuttrong = πH(R 2 + r 2 + Rr ) / 3 Vnoncutngoai = πH((R + b) 2 + (r + b) 2 + (R + b)(r + b)) / 3 Troïng löôïng bình: G = γ n δV = γ n δ(Vnoncutngoai − Vnoncuttrong ) = 1000 * 7.8 * 0.057 = 441.96kgf Ta tính löïc Fz höôùng leân do nöôùc taùc duïng leân bình: r Từ quan hệ: x = R − rx ⇒ r = R − x (R − r ) b x H R −r H ⎡ πx 2 2 ⎤ H Fz = γ n W = γ n ⎢R 2 πx − (R − rx + Rrx )⎥ rx ⎣ 3 ⎦ πx ⎡ 2 x x ⎤ x = γn ⎢2R − (R − H (R − r )) − R (R − H (R − r ))⎥ 2 W 3 ⎣ ⎦ πx ⎡ 3R (R − r ) ⎛ (R − r ) ⎞ ⎤ 2 R = γn ⎢ x −⎜ x ⎟ ⎥ = 392.7 x 2 − 16.36x 3 Fz 3 ⎢⎣ H ⎝ H ⎠ ⎥⎦ Ñieàu kieän: G ≥ Fz Suy ra: 441.96 ≥ Fz ⇔ 16.36x 3 − 392.7 x 2 + 441.96 ≥ 0 Giaûi ra ñöôïc x ≤ 1.09 m THUY TINH 19
  20. PGS.TS. Nguyen Thi Bay, DHBK tp. HCM; www4.hcmut.edu.vn/~ntbay VIII. TÓNH HOÏC TÖÔNG ÑOÁI z 1.Nöôùc trong xe chaïy tôùi tröôùc nhanh daàn ñeàu: x •Phaân boá aùp suaát: O α A 1 a (Fxdx+ Fydy+ Fzdz) − dp= 0 vôùi Fx=-a; Fy=0; Fz=-g H ρ B Suy ra: g* 1 p g (−adx − gdz) − dp = 0 ⇒ ax + gz + = C ρ ρ Ñoái vôùi hai ñieåm A,B thaúng ñöùng: pA p + gzA = B + gzB ⇒ pB = pA + γhAB hay p = pa + γh* ρ ρ •P.tr Maët ñaúng aùp: a (−adx − gdz) = 0 ⇒ ax + gz = C ⇒ z = − x+C g 2.Nöôùc trong bình truï quay ñeàu quanh truïc thaúng ñöùng: z •Phaân boá aùp suaát: H/2 H ÔÛ ñaây: Fx=ω2x; Fy=ω2y; Fz=-g. H/2 O A r ω2r Suy ra: 1 p ω2r2 B (ω2xdx+ ω2 ydy− gdz) − dp = 0 ⇒ z + − =C ρ γ 2g g ω Ñoái vôùi hai ñieåm A,B thaúng ñöùng: 2 2 pA ω2rA pB ω2rB * zA + − = zB + − ⇒pB = pA + γhAB hay p = pa + γh γ 2g γ 2g •P.tr Maët ñaúng aùp: ω2r 2 ω2r 2 (ω xdx+ ω ydy− gdz) = 0 ⇒ z − 2 2 = C ⇒z = +C 2g 2g THUY TINH 20
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
4=>1