1
1
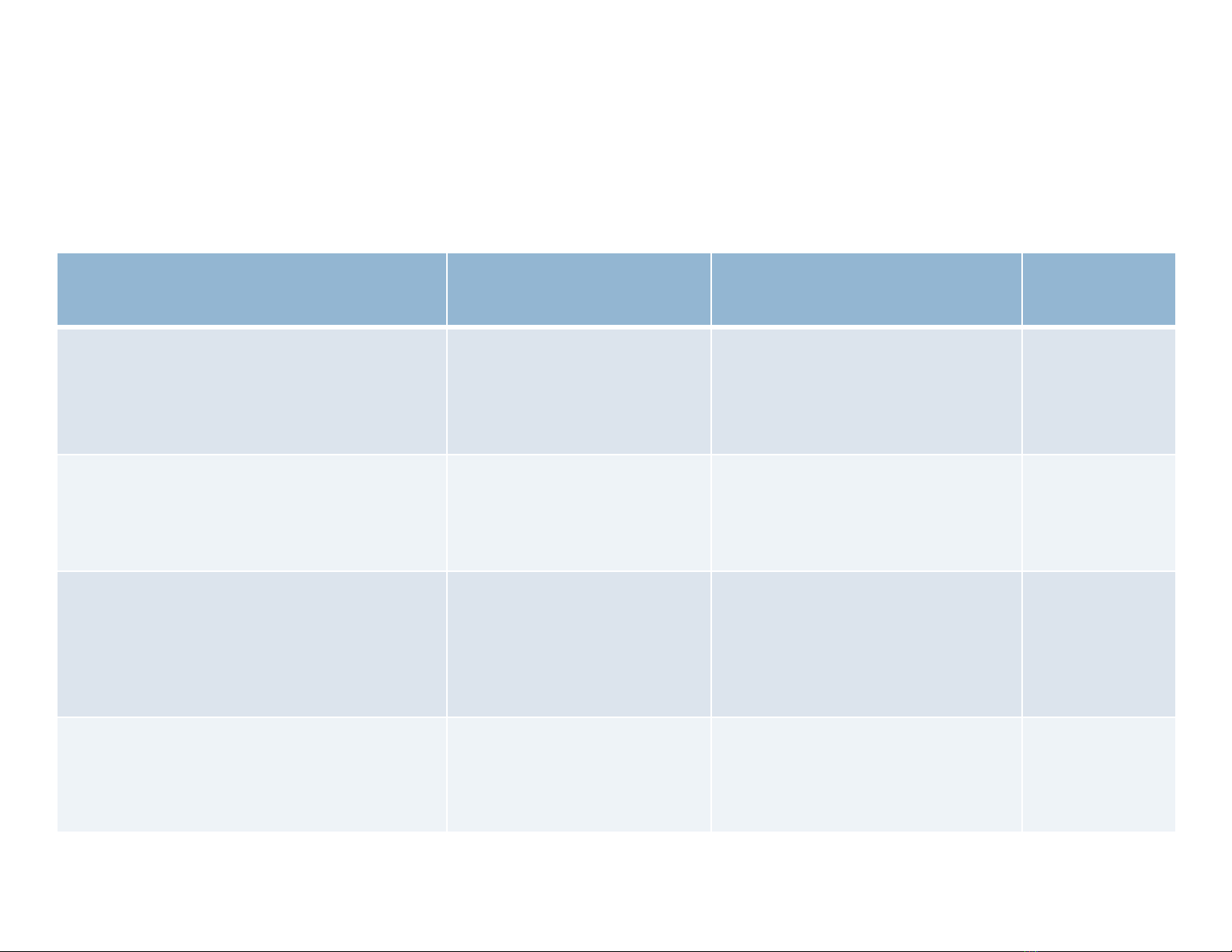
GIẢ THIẾT NỘI DUNG KHUYẾT TẬT MỤC
Mô hình đinh dạng
đúng
Mô hình định dạng sai
(chỉ định sai)
5.1 và 5.5
Phươngsai sai số
đồng đều
Phươngsai sai số thay
đổi 5.2
Các biến độc lập
không có tương quan
tuyến tính
Đa cộng tuyến 5.4
Sai số ngẫu nhiên
phân phối chuẩn
Sai số ngẫu nhiên không
phân phối chuẩn
5.3
CƠ SỞ ĐÁNH GIÁ MÔ HÌNH
CÁC GIẢ THIẾT CỦA PHƯƠNG PHÁP OLS
0),...,,/( 32
kiiii XXXUE
2
32 ),...,,/var(
kiiii XXXU
0),cov(
iji UX
0
...
3322
kikii XXX
),0(~ 2
NUi
2
5.1. KỲ VỌNG CỦA SAI SỐ NGẪU NHIÊN KHÁC KHÔNG
5.1.1. NGUYÊN NHÂN
5.1.2. HẬU QUẢ
5.1.3. PHÁT HIỆN
5.1.4. KHẮC PHỤC

3
5.1. KỲ VỌNG CỦA SAI SỐ NGẪU NHIÊN KHÁC KHÔNG
NGUYÊN NHÂN
Nguyên nhân 1: Mô hình thiếu biến quan trọng
-Biến Z có tác động đến Y
Mô hình đúng:
Mô hình sai:
- Biến Z có tương quan với ít nhất một biến độc lập
iikikmimiii uZXXXXY
.......
33221
ikikmimiii vXXXXY
......
33221
0),cov(0),cov( 22
vXZX

4
5.1. KỲ VỌNG CỦA SAI SỐ NGẪU NHIÊN KHÁC KHÔNG
NGUYÊN NHÂN
kikmimiikimiii XXXXXXXXYE
......),...,,...,,/( 3322132
ikikmimiii uXXXXY
......
33221
Nguyên nhân 2: Dạng hàm sai
nếu thỏa mãn: thì sẽ có:
nhưng các phương trình sau lại không thỏa mãn:
0),...,,/( 32
kiiii XXXUE
iikikiikiii uXXXXXXYE 2
2332212 ...),...,/(
ikikiikiii uXXXXXYE
)log(....)log(.)log(.),...,/( 332212

5
5.1. KỲ VỌNG CỦA SAI SỐ NGẪU NHIÊN KHÁC KHÔNG
NGUYÊN NHÂN
Nguyên nhân 3: Tính tác động đồng thời của số liệu
Nguyên nhân 4: Sai số do đo lường số liệu


























