1
1
2D Transformations
2D Transformations
Các phép bi n đ i 2Dế ổ
Các phép bi n đ i 2Dế ổ
2
2
•B n ch t c a phép bi n đ i hình h c là thay đ i v trí c a đ i t ng, ả ấ ủ ế ổ ọ ổ ị ủ ố ượ
B n ch t c a phép bi n đ i hình h c là thay đ i v trí c a đ i t ng, ả ấ ủ ế ổ ọ ổ ị ủ ố ượ
làm thay đ i đ i t ng v h ng, kích th c, hình d ng.ổ ố ượ ề ướ ướ ạ
làm thay đ i đ i t ng v h ng, kích th c, hình d ng.ổ ố ượ ề ướ ướ ạ
•Hai ph ng pháp đ bi n đ i hình h c:ươ ể ế ổ ọ
Hai ph ng pháp đ bi n đ i hình h c:ươ ể ế ổ ọ
–Bi n đ i đ i t ng: thay đ i t a đ c a đ i t ng.ế ổ ố ượ ổ ọ ộ ủ ố ượ
Bi n đ i đ i t ng: thay đ i t a đ c a đ i t ng.ế ổ ố ượ ổ ọ ộ ủ ố ượ
–Bi n đ i h t a đ : t o h t a đ m i và t t c đ i t ng s đ c ế ổ ệ ọ ộ ạ ệ ọ ộ ớ ấ ả ố ượ ẽ ượ
Bi n đ i h t a đ : t o h t a đ m i và t t c đ i t ng s đ c ế ổ ệ ọ ộ ạ ệ ọ ộ ớ ấ ả ố ượ ẽ ượ
chuy n v h t a đ m i.ể ề ệ ọ ộ ớ
chuy n v h t a đ m i.ể ề ệ ọ ộ ớ
•Các phép bi n đ i hình h c c b n: t nh ti n, quay, bi n đ i t l , ế ổ ọ ơ ả ị ế ế ổ ỉ ệ
Các phép bi n đ i hình h c c b n: t nh ti n, quay, bi n đ i t l , ế ổ ọ ơ ả ị ế ế ổ ỉ ệ
bi n d ng.ế ạ
bi n d ng.ế ạ
Gi i thi uớ ệ
Gi i thi uớ ệ
3
3
•M t phép bi n đ i là m t ánh x ộ ế ổ ộ ạ
M t phép bi n đ i là m t ánh x ộ ế ổ ộ ạ T
T:
:
Phép bi n đ i hình h cế ổ ọ
Phép bi n đ i hình h cế ổ ọ
)','(),(
:
22
yxQyxP
RRT
→
P(x,y)
Q(x’,y’)
=
=
),('
),('
yxgy
yxfx
4
4
•Phép bi n đ i Affine là phép bi n đ i v i f(x,y) và g(x,y) là 2 ế ổ ế ổ ớ
Phép bi n đ i Affine là phép bi n đ i v i f(x,y) và g(x,y) là 2 ế ổ ế ổ ớ
hàm tuy n tính:ế
hàm tuy n tính:ế
•Bi u di n phép bi n đ i Affine d i d ng ma tr n:ể ễ ế ổ ướ ạ ậ
Bi u di n phép bi n đ i Affine d i d ng ma tr n:ể ễ ế ổ ướ ạ ậ
•Thông th ng, chúng ta ch kh o sát phép bi n Affine nên ta ườ ỉ ả ế
Thông th ng, chúng ta ch kh o sát phép bi n Affine nên ta ườ ỉ ả ế
th ng dùng thu t ng phép bi n đ i đ ng ý là phép bi n ườ ậ ữ ế ổ ể ụ ế
th ng dùng thu t ng phép bi n đ i đ ng ý là phép bi n ườ ậ ữ ế ổ ể ụ ế
đ i Affine.ổ
đ i Affine.ổ
Phép bi n đ i hình h c (cont.)ế ổ ọ
Phép bi n đ i hình h c (cont.)ế ổ ọ
++=
++=
feydxy
cbyaxx
'
'
PTQy
x
fed
cba
y
x
.
11001
'
'
=⇔
=
5
5
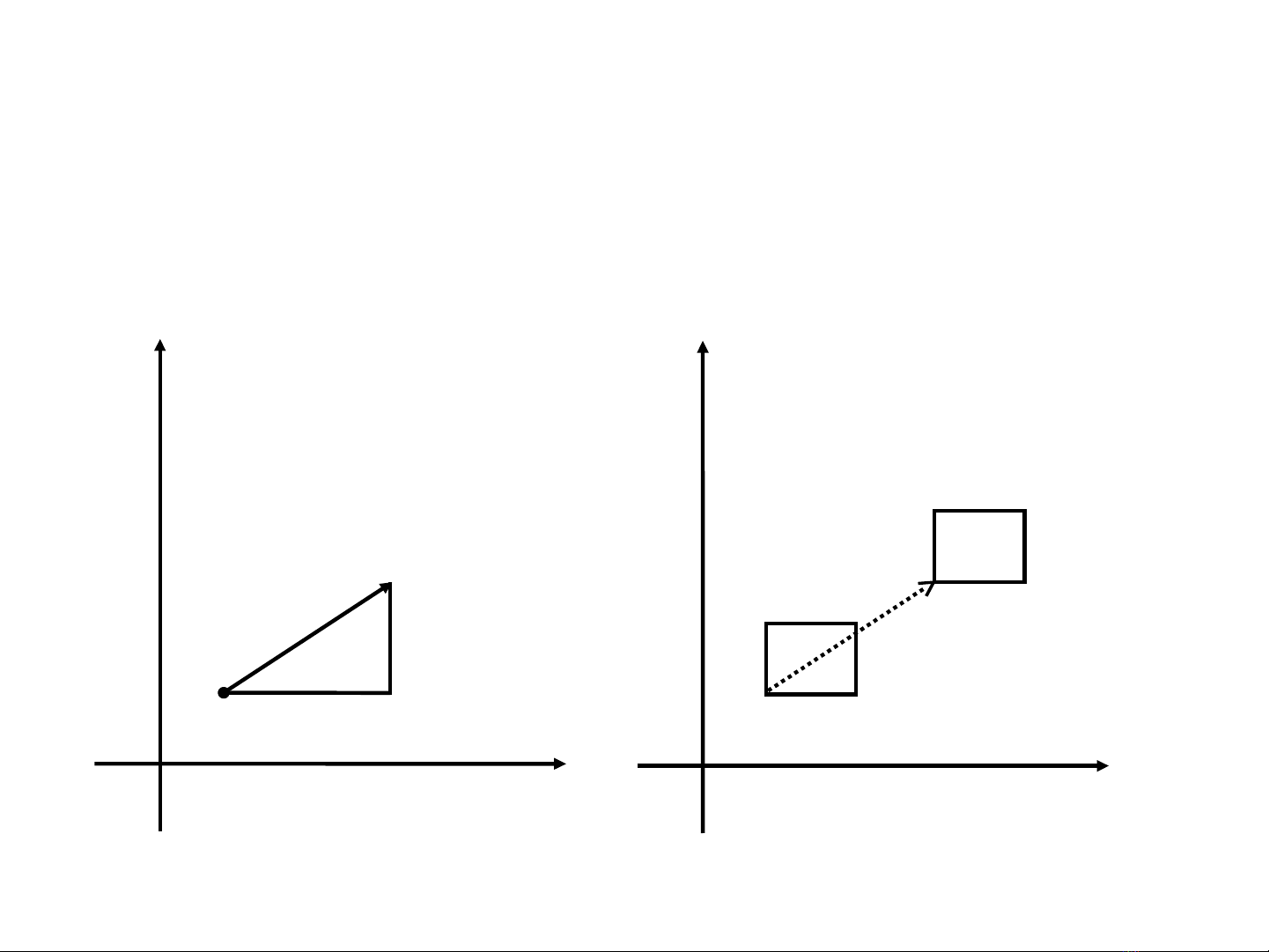
•Phép t nh ti n dùng đ d ch chuy n đ i t ng t v trí này sang ị ế ể ị ể ố ượ ừ ị
Phép t nh ti n dùng đ d ch chuy n đ i t ng t v trí này sang ị ế ể ị ể ố ượ ừ ị
v trí khác.ị
v trí khác.ị
Phép t nh ti n - Translationị ế
Phép t nh ti n - Translationị ế
trx
try
P
Q