1
1
Projection
Projection
Phép chi uế
Phép chi uế
2
2
Plane Projection
Plane Projection
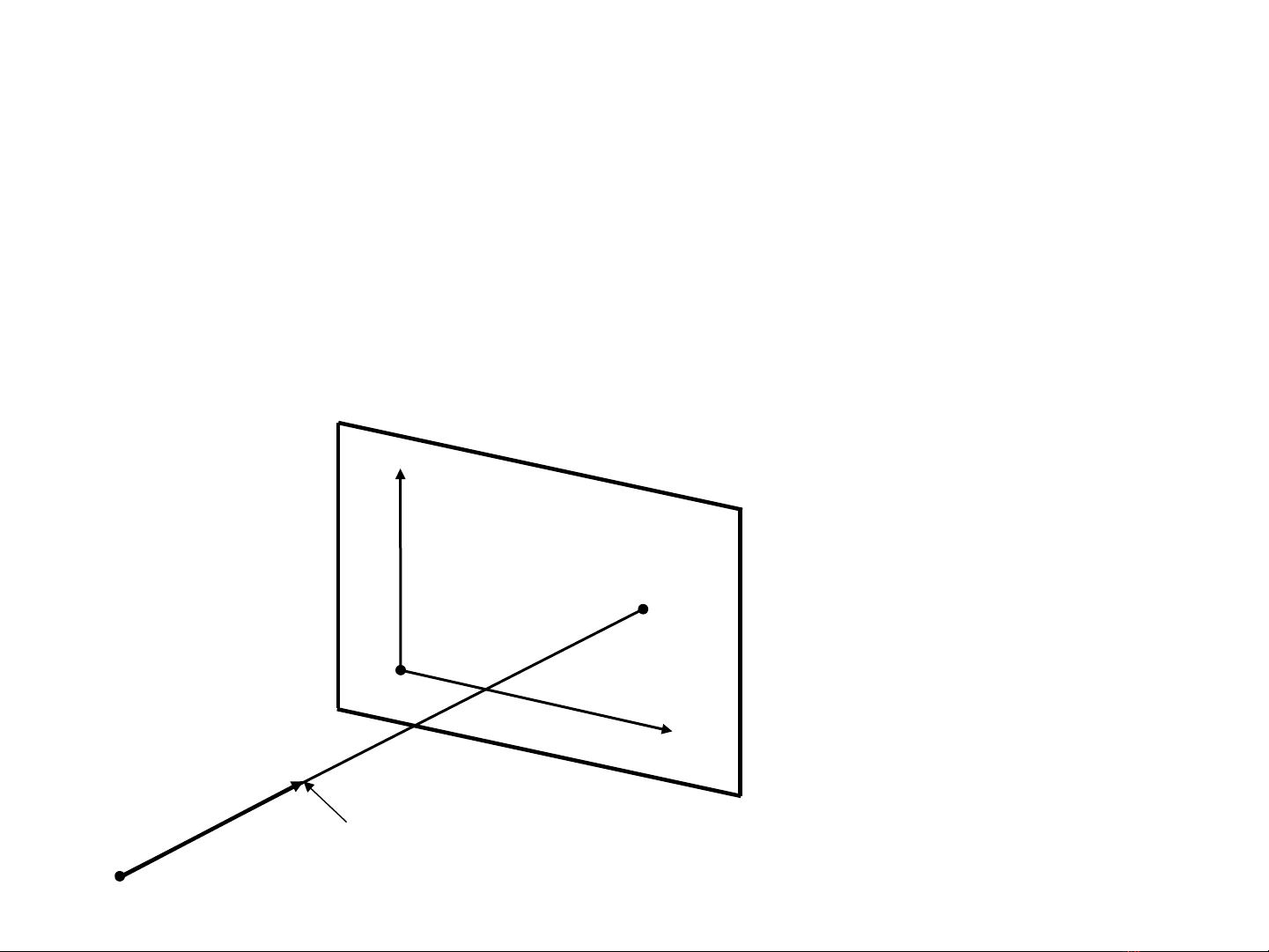
•Đ hi n th các đ i t ng 3D trong thi t b hi n th 2D.ể ể ị ố ượ ế ị ể ị
Đ hi n th các đ i t ng 3D trong thi t b hi n th 2D.ể ể ị ố ượ ế ị ể ị
•Trong phép chi u ph ng, m i đi m đ i t ng – ế ẳ ỗ ể ố ượ
Trong phép chi u ph ng, m i đi m đ i t ng – ế ẳ ỗ ể ố ượ object
object
point
point – đ c chi u trên m t ph ng nh – ượ ế ặ ẳ ả
– đ c chi u trên m t ph ng nh – ượ ế ặ ẳ ả picture plane
picture plane
(view plane)
(view plane), chúng ta đ c m t đi m nh – ượ ộ ể ả
, chúng ta đ c m t đi m nh – ượ ộ ể ả picture point
picture point.
.
u2
u1
r0
r object point
r’ picture point
Projection line
Picture
plane
u
3
3
M
Mt ph ng chi uặ ẳ ế
t ph ng chi uặ ẳ ế
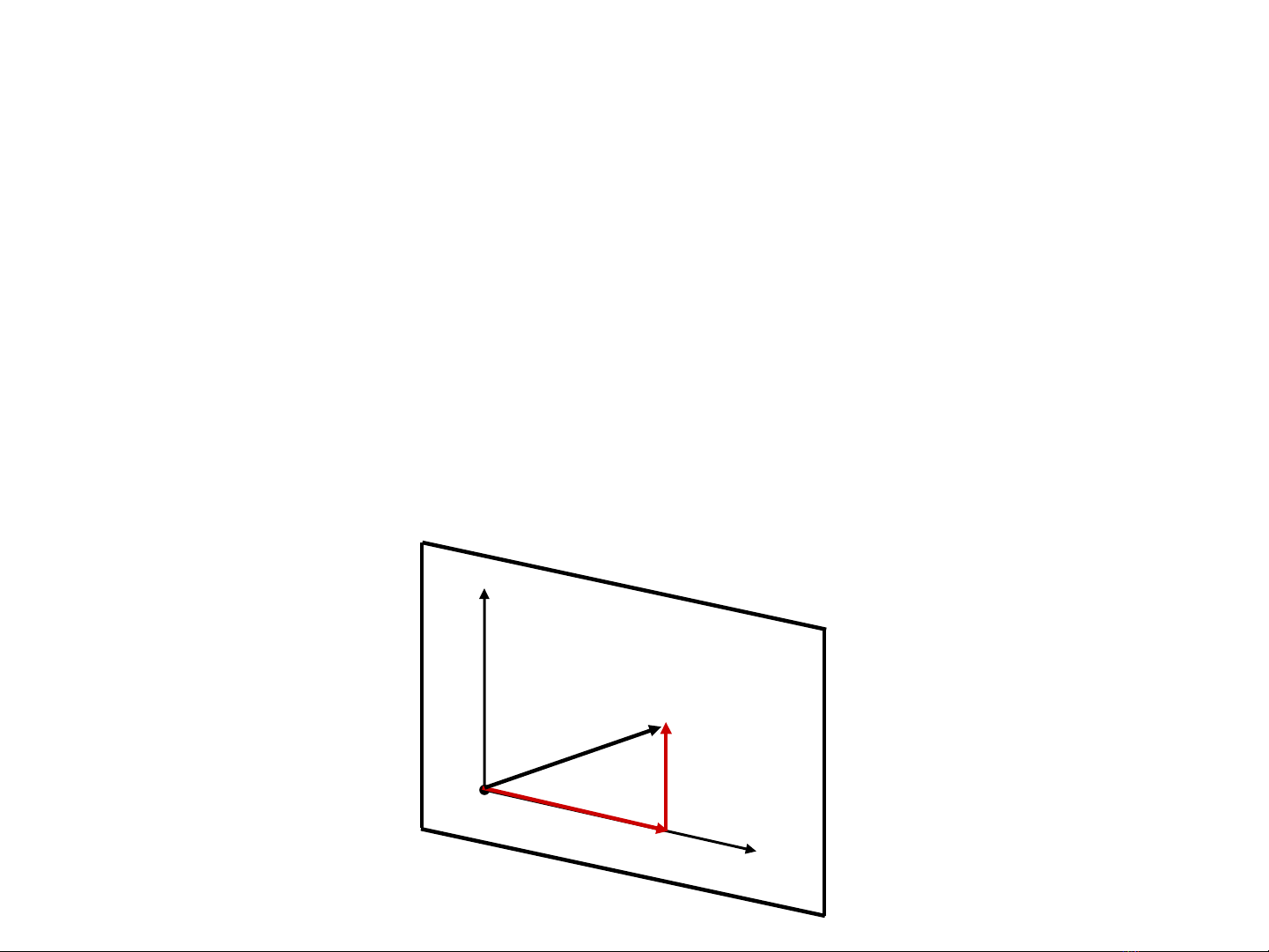
M t ph ng chi u có g c ặ ẳ ế ố
M t ph ng chi u có g c ặ ẳ ế ố r
r0
0 và 2 vect đ n v ơ ơ ị
và 2 vect đ n v ơ ơ ị u
u1
1 và
và u
u2
2
V i đi m r’ trên m t ph ng chi u, ta có vect ớ ể ặ ẳ ế ơ
V i đi m r’ trên m t ph ng chi u, ta có vect ớ ể ặ ẳ ế ơ (r’ – r
(r’ – r0
0)
) đ c ượ
đ c ượ
phân tích theo 2 vect đ n v :ơ ơ ị
phân tích theo 2 vect đ n v :ơ ơ ị
r’ – r
r’ – r0
0 = x’ u1 + y’ u2
= x’ u1 + y’ u2
Khi đó
Khi đó (x’, y’)
(x’, y’) là t a đ c a ọ ộ ủ
là t a đ c a ọ ộ ủ r’
r’ trên m t ph ng chi u.ặ ẳ ế
trên m t ph ng chi u.ặ ẳ ế
u2
u1
r0
r’
x’u1
y’u2
4
4
Plane Parallel Projection
Plane Parallel Projection
Phép chi u song songế
Phép chi u song songế
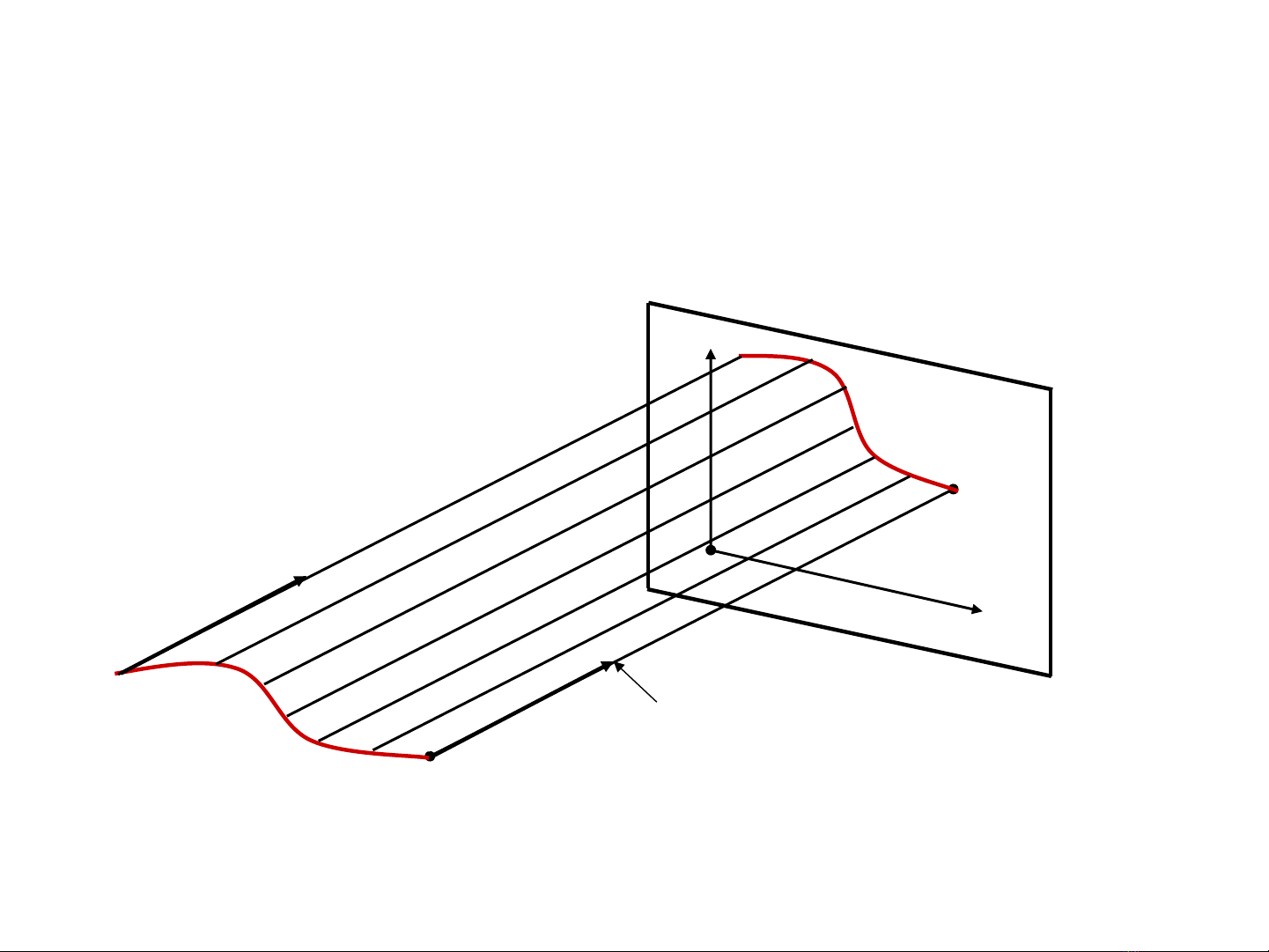
•Các đ ng th ng chi u song song v i nhau.ườ ẳ ế ớ
Các đ ng th ng chi u song song v i nhau.ườ ẳ ế ớ
u2
u1
r0
r
r’
Projection line
u
u
5
5
Plane Parallel Projection
Plane Parallel Projection
(cont)
(cont)
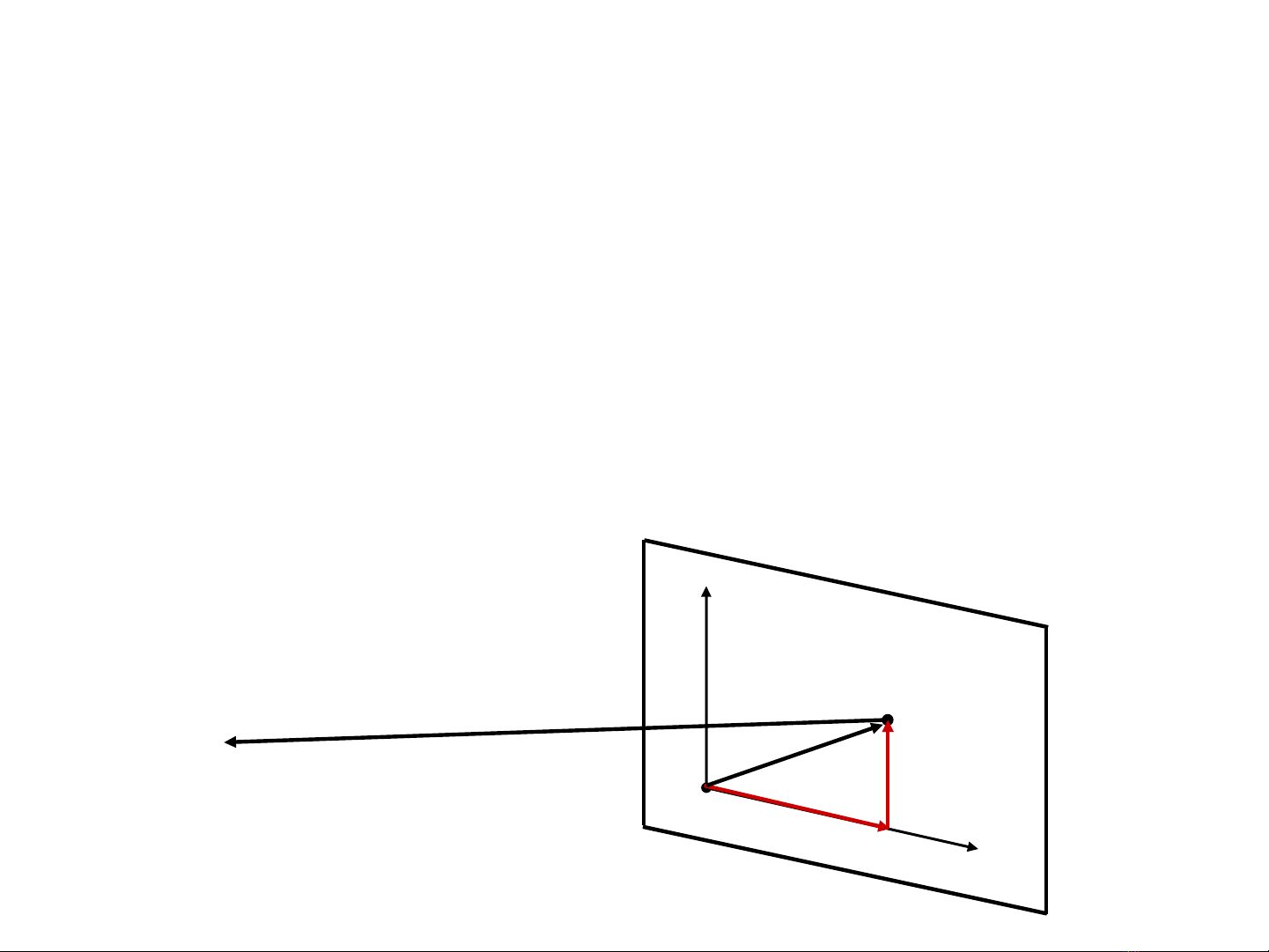
M i đi m r đ c chi u song song theo ph ng u vào m t ỗ ể ượ ế ươ ặ
M i đi m r đ c chi u song song theo ph ng u vào m t ỗ ể ượ ế ươ ặ
ph ng chi u, ta đ c đi m nh r’:ẳ ế ượ ể ả
ph ng chi u, ta đ c đi m nh r’:ẳ ế ượ ể ả
∃
∃! z’ : r’ = r – z’u
! z’ : r’ = r – z’u
r’ là đi m nh n m trên m t ph ng chi u:ể ả ằ ặ ẳ ế
r’ là đi m nh n m trên m t ph ng chi u:ể ả ằ ặ ẳ ế
∃
∃! x’, y’ : r’ = r
! x’, y’ : r’ = r0
0 + x’u
+ x’u1
1 + y’u
+ y’u2
2
Do đó:
Do đó:
r – z’u = r
r – z’u = r0
0 + x’u
+ x’u1
1 + y’u
+ y’u2
2
(1)
(1)
u2
u1
r0
rr’
z’u
x’u1
y’u2