1
1
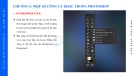
Thu t toán v đ ng th ng Bresenhamậ ẽ ườ ẳ
Thu t toán v đ ng th ng Bresenhamậ ẽ ườ ẳ
2
2
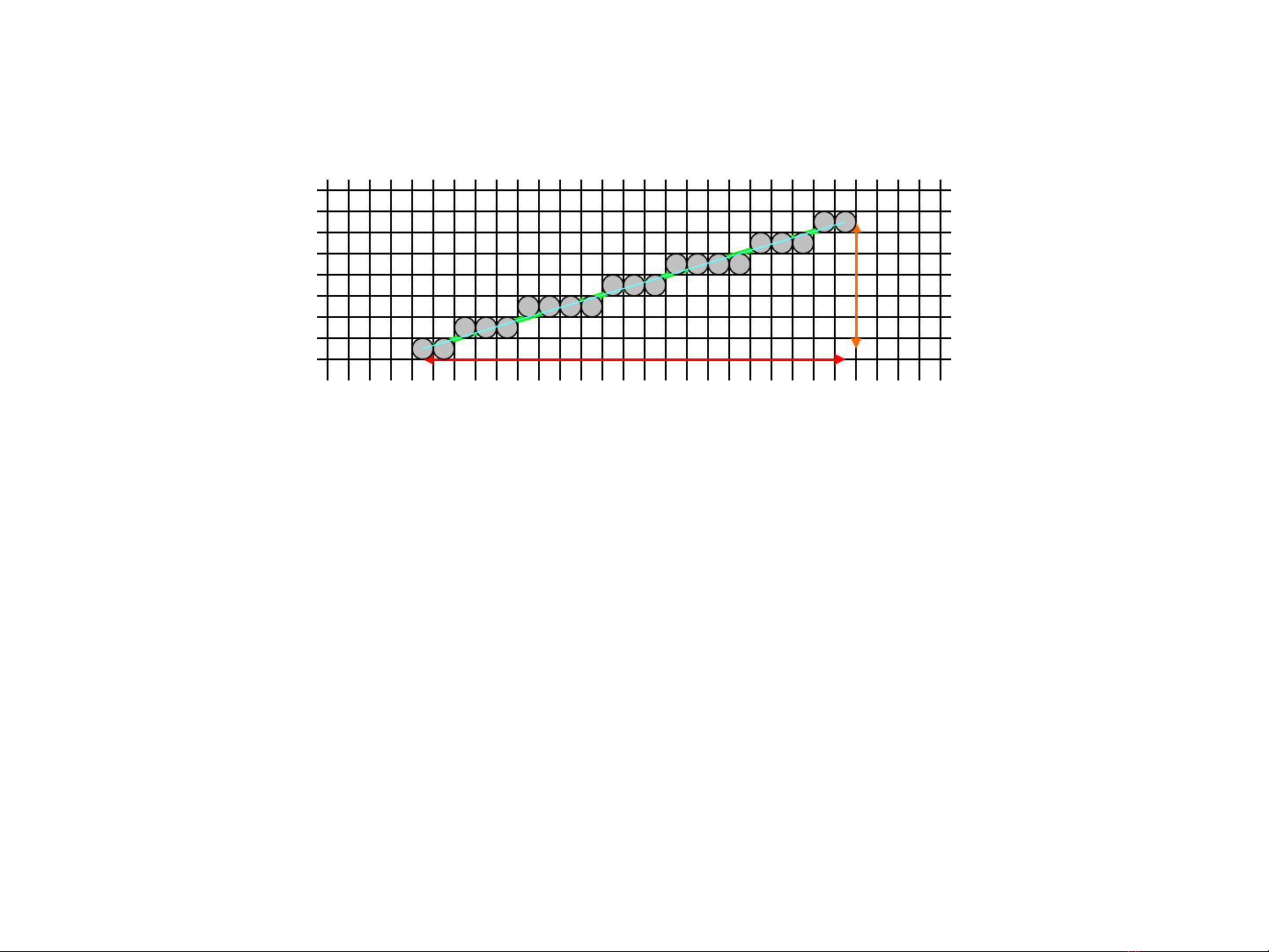
M i t ng quan gi a X & Yố ươ ữ
M i t ng quan gi a X & Yố ươ ữ
khi đ l n h s góc nh h n 1ộ ớ ệ ố ỏ ơ
khi đ l n h s góc nh h n 1ộ ớ ệ ố ỏ ơ
x tăng 1 và y gi nguyên hay tăng 1ữ
x tăng 1 và y gi nguyên hay tăng 1ữ
Đi u này b o đ m cho đ ng th ng ề ả ả ườ ẳ
Đi u này b o đ m cho đ ng th ng ề ả ả ườ ẳ liên t cụ
liên t cụ
N u đ l n c a h s góc l n h n 1, chúng ta đ i vai trò c a x ế ộ ớ ủ ệ ố ớ ơ ổ ủ
N u đ l n c a h s góc l n h n 1, chúng ta đ i vai trò c a x ế ộ ớ ủ ệ ố ớ ơ ổ ủ
& y
& y
x đ c g i là giá tr đ c l p và y là ượ ọ ị ộ ậ
x đ c g i là giá tr đ c l p và y là ượ ọ ị ộ ậ giá tr ph thu cị ụ ộ
giá tr ph thu cị ụ ộ
Dx
Dy
3
3
Thu t toán Bresenhamậ
Thu t toán Bresenhamậ
Gi i thi u:ớ ệ
Gi i thi u:ớ ệ
•Gi s đ ng cong đ c x p x thành các đi m l n l t là ả ử ườ ượ ấ ỉ ể ầ ượ
Gi s đ ng cong đ c x p x thành các đi m l n l t là ả ử ườ ượ ấ ỉ ể ầ ượ
(x
(xi
i,y
,yi
i)
). Các đi m này có t a đ nguyên và đ c hi n th trên ể ọ ộ ượ ể ị
. Các đi m này có t a đ nguyên và đ c hi n th trên ể ọ ộ ượ ể ị
màn hình.
màn hình.
•Bài toán đ t ra là n u bi t đ c t a đ (xặ ế ế ượ ọ ộ
Bài toán đ t ra là n u bi t đ c t a đ (xặ ế ế ượ ọ ộ i
i,y
,yi
i) c a b c th i, thì ủ ướ ứ
) c a b c th i, thì ủ ướ ứ
đi m b c i+1 là (xể ở ướ
đi m b c i+1 là (xể ở ướ i+1
i+1,y
,yi+1
i+1) s đ c xác đ nh nh th nào. ẽ ượ ị ư ế
) s đ c xác đ nh nh th nào. ẽ ượ ị ư ế
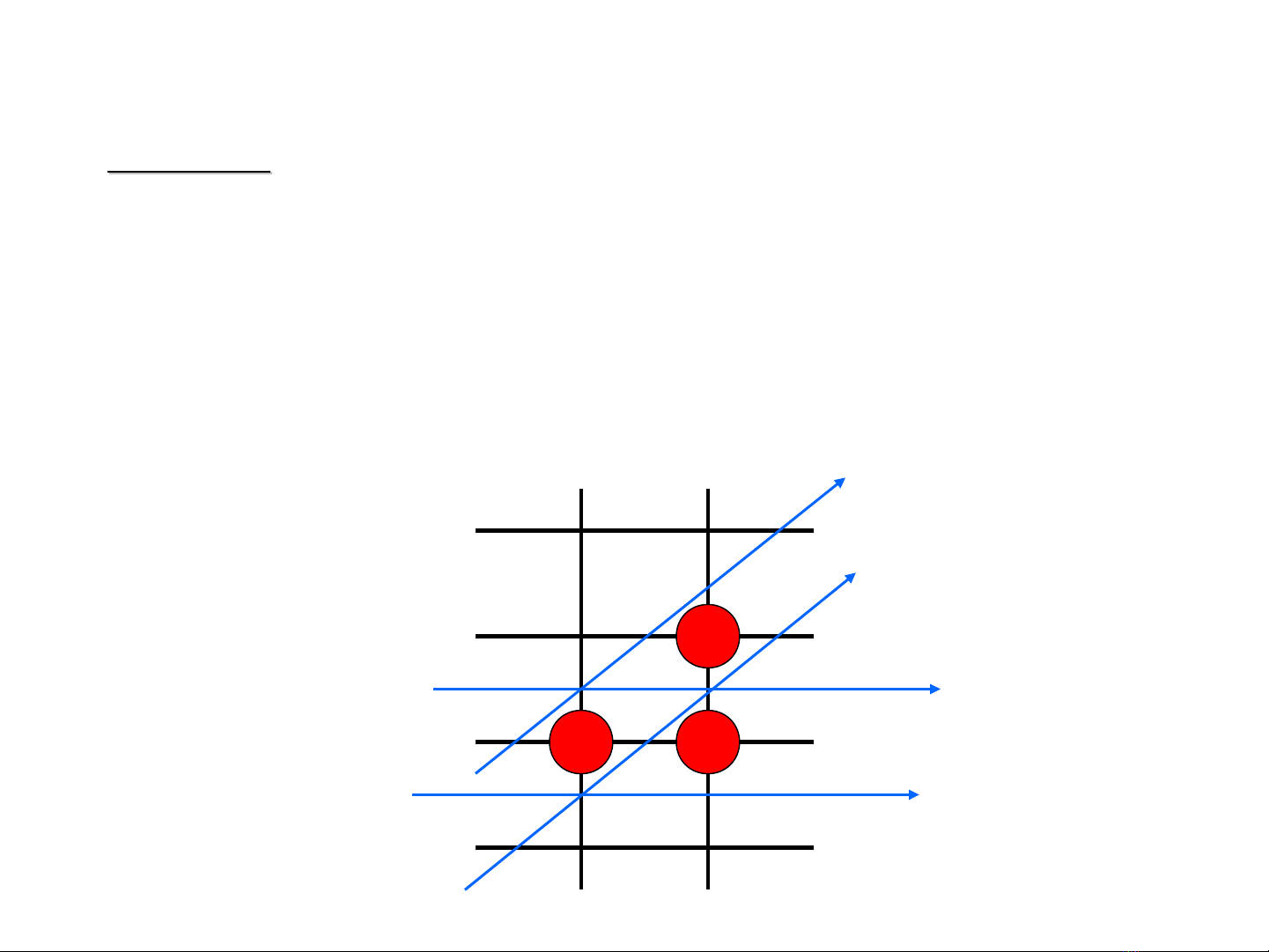
•Trong tr ng h p h s góc 0<=m<=1, chúng ta có xườ ợ ệ ố
Trong tr ng h p h s góc 0<=m<=1, chúng ta có xườ ợ ệ ố i+1
i+1=x
=xi
i+1 và
+1 và
y
yi+1
i+1=y
=yi
i hay y
hay yi+1
i+1=y
=yi
i+1
+1
xi
yi
yi+1
yi-1
xi+1
4
4
Thu t toánậ
Thu t toánậ
•Ph ng trình đ ng th ng qua 2 đi m (xươ ườ ẳ ể
Ph ng trình đ ng th ng qua 2 đi m (xươ ườ ẳ ể 1
1, y
, y1
1) và (x
) và (x2
2, y
, y2
2) là
) là
y=mx+b v i m=Dy/Dx và b=yớ
y=mx+b v i m=Dy/Dx và b=yớ1
1-mx
-mx1
1.
.
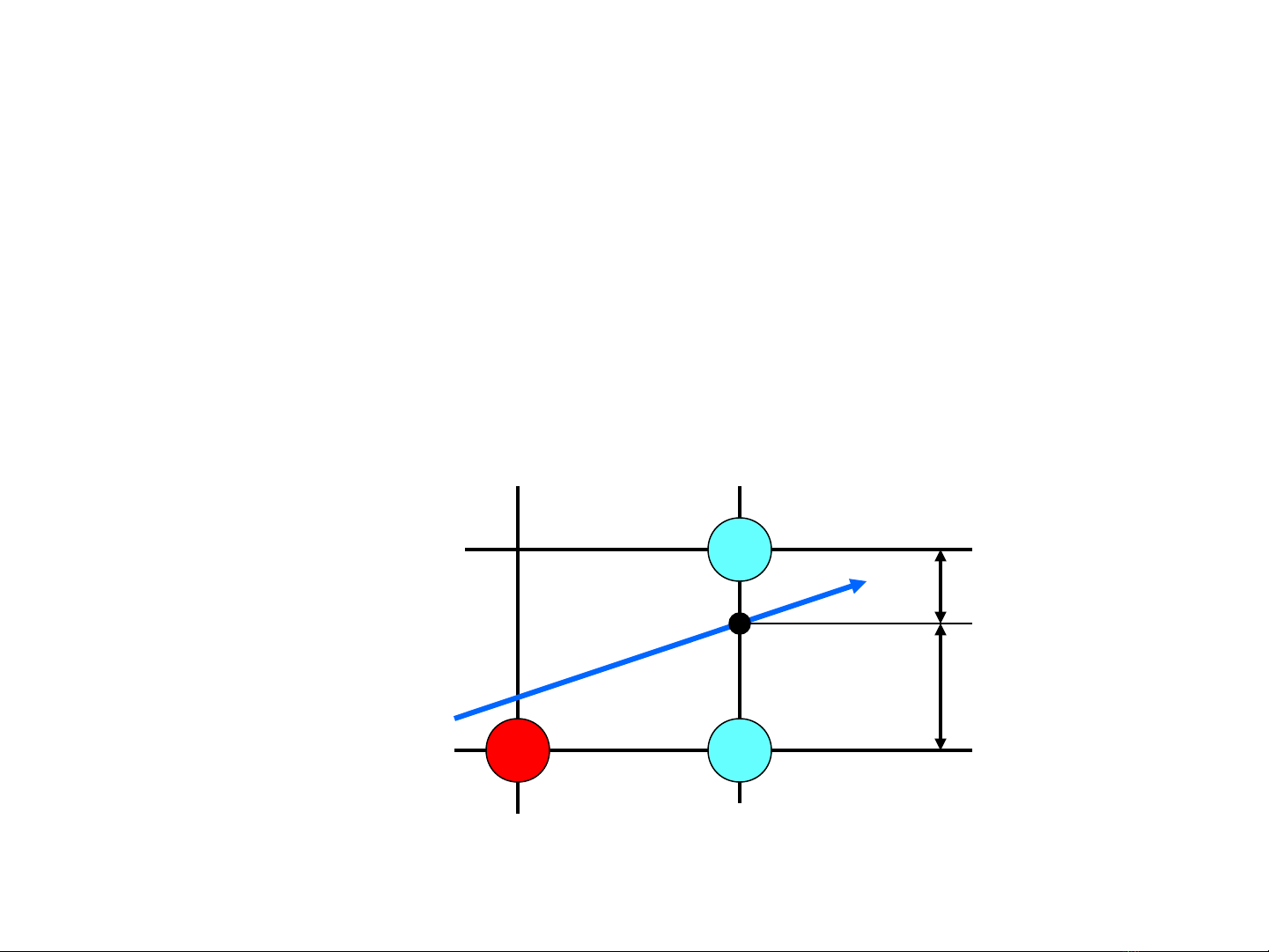
•Đ t dặ
Đ t dặ1
1=y-y
=y-yi
i và d
và d2
2=(y
=(yi
i+1)-y, do đó vi c ch n t a đ c a yệ ọ ọ ộ ủ
+1)-y, do đó vi c ch n t a đ c a yệ ọ ọ ộ ủ i+1
i+1 ph ụ
ph ụ
thu c vào dộ
thu c vào dộ1
1 và d
và d2
2 ( hay d u c a dấ ủ
( hay d u c a dấ ủ 1
1 - d
- d2
2):
):
–N u dế
N u dế1
1-d
-d2
2<0 thì ch n yọ
<0 thì ch n yọi+1
i+1=y
=yi
i
–Ng c l i, ch n yượ ạ ọ
Ng c l i, ch n yượ ạ ọ i+1
i+1=y
=yi
i+1
+1
xi
yi
yi+1 P
xi+1=xi+1
S
d2
d1
(xi+1,y=f(xi+1))
5
5
Thu t toán (cont.)ậ
Thu t toán (cont.)ậ
•d
d1
1 - d
- d2
2 = (2y – 2y
= (2y – 2yi
i – 1) là m t s th c do ch a ộ ố ự ứ
– 1) là m t s th c do ch a ộ ố ự ứ m
m
•Xét p
Xét pi
i = Dx (d
= Dx (d1
1 - d
- d2
2) = Dx (2y - 2y
) = Dx (2y - 2yi
i - 1) = 2Dy x
- 1) = 2Dy xi
i - 2Dx y
- 2Dx yi
i + C
+ C
–C = 2Dy + (2b - 1)Dx
C = 2Dy + (2b - 1)Dx
•Do d u c a pấ ủ
Do d u c a pấ ủ i
i và (d
và (d1
1-d
-d2
2) gi ng nhau nên khi xét d u c a pố ấ ủ
) gi ng nhau nên khi xét d u c a pố ấ ủ i
i thì ta
thì ta
xác đ nh đ c yị ượ
xác đ nh đ c yị ượ i+1
i+1
•M c khác, pặ
M c khác, pặi+1
i+1 – p
– pi
i = (2Dy x
= (2Dy xi+1
i+1 - 2Dx y
- 2Dx yi+1
i+1 + C) - (2Dy x
+ C) - (2Dy xi
i - 2Dx y
- 2Dx yi
i + C)
+ C)
= 2Dy – 2Dx(y
= 2Dy – 2Dx(yi+1
i+1 – y
– yi
i)
)
•T đây, ta suy ra cách tính pừ
T đây, ta suy ra cách tính pừi+1
i+1 theo p
theo pi
i:
:
–N u pế
N u pếi
i<0 thì y
<0 thì yi+1
i+1=y
=yi
i nên p
nên pi+1
i+1 = p
= pi
i + 2Dy
+ 2Dy
–Ng c l i thì yượ ạ
Ng c l i thì yượ ạ i+1
i+1=y
=yi
i+1 nên p
+1 nên pi+1
i+1 = p
= pi
i + 2Dy – 2Dx
+ 2Dy – 2Dx
•Giá tr p đ u tiên đ c tính t i (xị ầ ượ ạ
Giá tr p đ u tiên đ c tính t i (xị ầ ượ ạ 1
1, y
, y1
1) là p
) là p1
1 = 2Dy x
= 2Dy x1
1 -2Dx y
-2Dx y1
1 + C =
+ C =
2Dy – Dx
2Dy – Dx