Chương8: Biến đổi Fourier
8.1. Phân tích chuổi Fourier
8.2. Các hệ số khai triển Fourier
8.3. Biến đổi dạng lượng lượng giác 3 thành phần
8.4.Áp dụng chuổi Fourier để phân tích mạch
8.5.Trị hiệu dụng hàm tuần hoàn
8.6.Công suất trung bình P
8.7.Chuổi Fourier dạng hàm mũ
8.8.Phổ biên độ và phổ pha rời rạc
CuuDuongThanCong.com https://fb.com/tailieudientucntt
8.1.Phân tích chuổi Fourier
f(t): Hàm tuần hoàn có chu kỳ T có thể được biểu diễn bởi chuỗi
Fourier dạng lượng giác 3 thành phần (dạng chuẩn):
*Với n là các số nguyên 1,2,3, …
*av , an , bn gọi là các hệ số khai triển Fourier.
*ω0 = 2л/T: gọi là tần số cơ bản ; các tần số là bội của ω gọi là
sóng hài như 2ω là sóng hài bậc 2; 3ω là sóng hài bậc 3..v.v..
*Ta có thể phân tích nguồn kích thích tuần hoàn thành chuổi
Fourier gồm thành phần một chiều av + tổng các thành phần điều
hòa (an và bn ) và dùng nguyên lý xếp chồng để tìm đáp ứng xác
lập.
Ta xác định các hệ số khai triển Fourier như sau:
)1.9(sincos)( 0
1
0tnbtnaatf n
n
nv
CuuDuongThanCong.com https://fb.com/tailieudientucntt
8.2. Các hệ số khai triển Fourier
Ta lưu ý các trị giá của các tích phân sau:
)4.9(sin)(
2
)3.9(cos)(
2
)2.9()(
1
0
0
0
0
0
0
0
0
dttktf
T
b
dttktf
T
a
dttf
T
a
Tt
t
k
Tt
t
k
Tt
t
v
CuuDuongThanCong.com https://fb.com/tailieudientucntt
nm
T
nmdttntm
nm
T
nmdttntm
dttntm
dttm
dttm
Tt
t
Tt
t
Tt
t
Tt
t
Tt
t
;
2
;0coscos
;
2
;0sinsin
0sincos
0cos
0sin
0
0
0
0
0
0
0
0
0
0
00
00
00
0
0
CuuDuongThanCong.com https://fb.com/tailieudientucntt
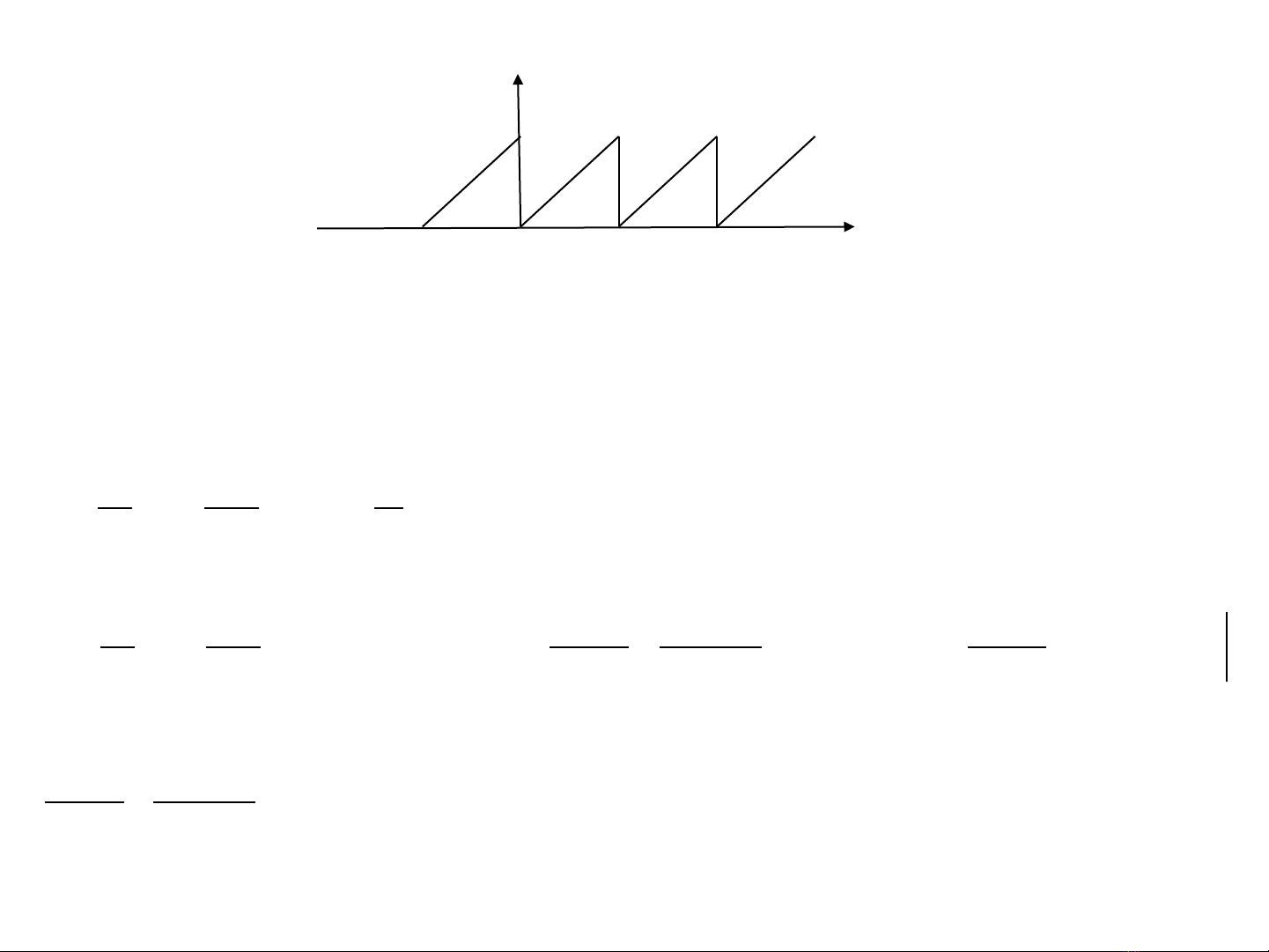
Ví dụ tìm chuổi Fourier của dạng sóng cho trước
Để tính các av; ak; bkta phải chọn to .Trong trường hợp này ta
nên chọn t0 = 0. Biểu thức v(t) trong khoảng 0 và T:v(t) = (Vm /T)t
v(t)
Vm
0
TT 2T
012cos
1
2
sincos
1
2
cos)(
2
2
1
)(
1
2
0
22
00
0
0
2
0
22
00
0
k
kT
V
tk
k
t
tk
kT
V
dttkt
T
V
T
a
Vtdt
T
V
T
a
m
T
m
Tm
k
m
Tm
v
CuuDuongThanCong.com https://fb.com/tailieudientucntt