HỆTRỢGIÚP QUYẾT ĐỊNH
Lớp HTTT + Pháp
Nămhọc 2009 - 2010
Bài 4, 5, 6 – Các mô hình ra quyếtđịnh
vớisựkhông chắcchắn
3.3. Các mô hình ra quyếtđịnh vớisựkhông chắcchắn:
NỘI DUNG :
-Ra quyếtđịnh đathuộctinh
-Toántửtích hợp
-Quanhệso sánh
TD Khang – ĐHBK Hà Nội
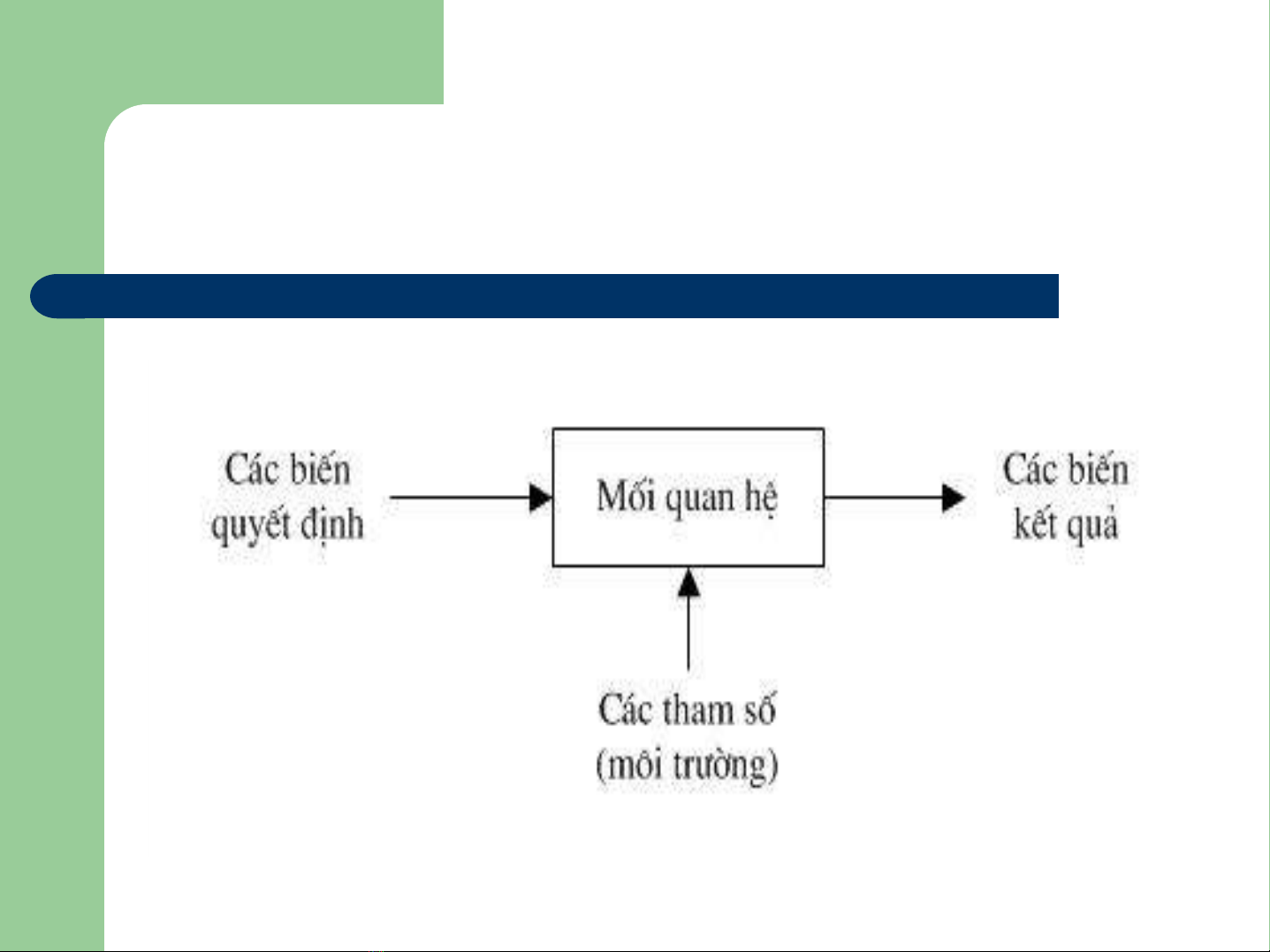
Mô hình bài toán đathuộc tính, đamục
tiêu, đa tiêu chuẩn
TD Khang – ĐHBK Hà Nội
A/ Ra quyếtđịnh đathuộc tính
Lựachọn trong sốcác phương án đượcđặctrưng bởi
nhiềuthuộctính
Dạng bảng biểudiễn giá trịcủacácphương án tại các
thuộctínhtương ứng
| Các thuộctính
Các phương án | Các giá trị
TD Khang – ĐHBK Hà Nội
Thuộctính
zChuẩn hoá các giá trịcủamộtthuộctính
-Đơnđiệu:
tuyến tính: rij = xij / xj*, vớix
j* là giá trịlớnnhất
(lợi ích) (nhỏnhất-thuộc tính giá) trong miền
giá trịthuộctínhX
j
vectơ: rij = xij / (Σixij2)1/2
-Không đơnđiệu: rij = exp(-z2/2), z= (xij –x
j0) / σj
-Định tính
zTrọng sốcủacácthuộc tính: wj∈[0,1], Σwj=1