
Học Máy
(IT 4862)
ễhậ
Nguy
ễ
n N
hậ
t Quang
quangnn-fit@mail.hut.edu.vn
Trường Đại học Bách Khoa Hà Nội
Viện Công nghệ thông tin và truyền thông
Năm học 2011-2012
Nội
d
ô
h
Nội
d
ung m
ô
n
h
ọc:
Giới thiệu chun
g
g
Đánh giá hiệunăng hệthống họcmáy
Các phương pháp họcdựatrênxácsuất
Các
phương
pháp
học
dựa
trên
xác
suất
Các phương pháp họccógiámsát
Học
dựa
trên
các
láng
giềng
gần
nhất
(Nearest
Học
dựa
trên
các
láng
giềng
gần
nhất
(Nearest
neighbors learning)
Các
p
hươn
g
p
há
p
học khôn
g
g
iám sát
p g
pp
g
g
Lọccộng tác
Học
tăng
cường
2
Học Máy – IT 4862
Học
tăng
cường

Học dựa trên các láng giềng gần nhất
Mộtsốtên gọi khác củaphương pháp họcdựa trên các láng
giềng gầnnhất (Nearest neighbors learning)
•Instance-based learning
•Lazy learning
•
Memory
-
based learning
Memory
based
learning
Ý tưởng củaphương pháp họcdựa trên các láng giềng gầnnhất
•Vớim
ộ
tt
ập
các ví d
ụ
h
ọ
c
ộ
ập
ụ
ọ
─(Đơngiảnlà) lưulạicácvídụhọc
─Chưaxâydựng mộtmôhình(môtả) rõ ràng và tổng quát của
hàm
mục
tiêu
cần
học
hàm
mục
tiêu
cần
học
•Đốivớimộtvídụcần phân loại/dựđoán
─Xét quan hệgiữavídụđóvớicácvídụhọcđể gán giá trịcủa
3
Học Máy – IT 4862
hàm mụctiêu(một nhãn lớp, hoặcmộtgiátrịthực)

Học dựa trên các láng giềng gần nhất
Biểu diễn đầu vào của bài toán
•Mỗi ví dụ xđược biểu diễn là một vectơ
n
chiều tron
g
khôn
g
g
ian
ggg
các vectơ X∈Rn
•x= (x1,x2,…,xn), trong đó xi(∈R) là một số thực
Cể ả ể
C
ó th
ể
áp dụng được với c
ả
2 ki
ể
u bài toán học
•Bài toán phân lớp (classification)
─
Hàm m
ụ
c tiêu có
g
iá tr
ị
rời r
ạ
c
(
a discrete-valued tar
g
et function
)
ụgị ạ (
g)
─Đầu ra của hệ thống là một trong số các giá trị rời rạc đã xác định
trước (một trong các nhãn lớp)
•
Bài toán
dự đoán/hồi quy (prediction/regression)
•
Bài
toán
dự
đoán/hồi
quy
(prediction/regression)
─Hàm mục tiêu có giá trị liên tục (a continuous-valued target function)
─Đầu ra của hệ thống là một giá trị số thực
4
Học Máy – IT 4862
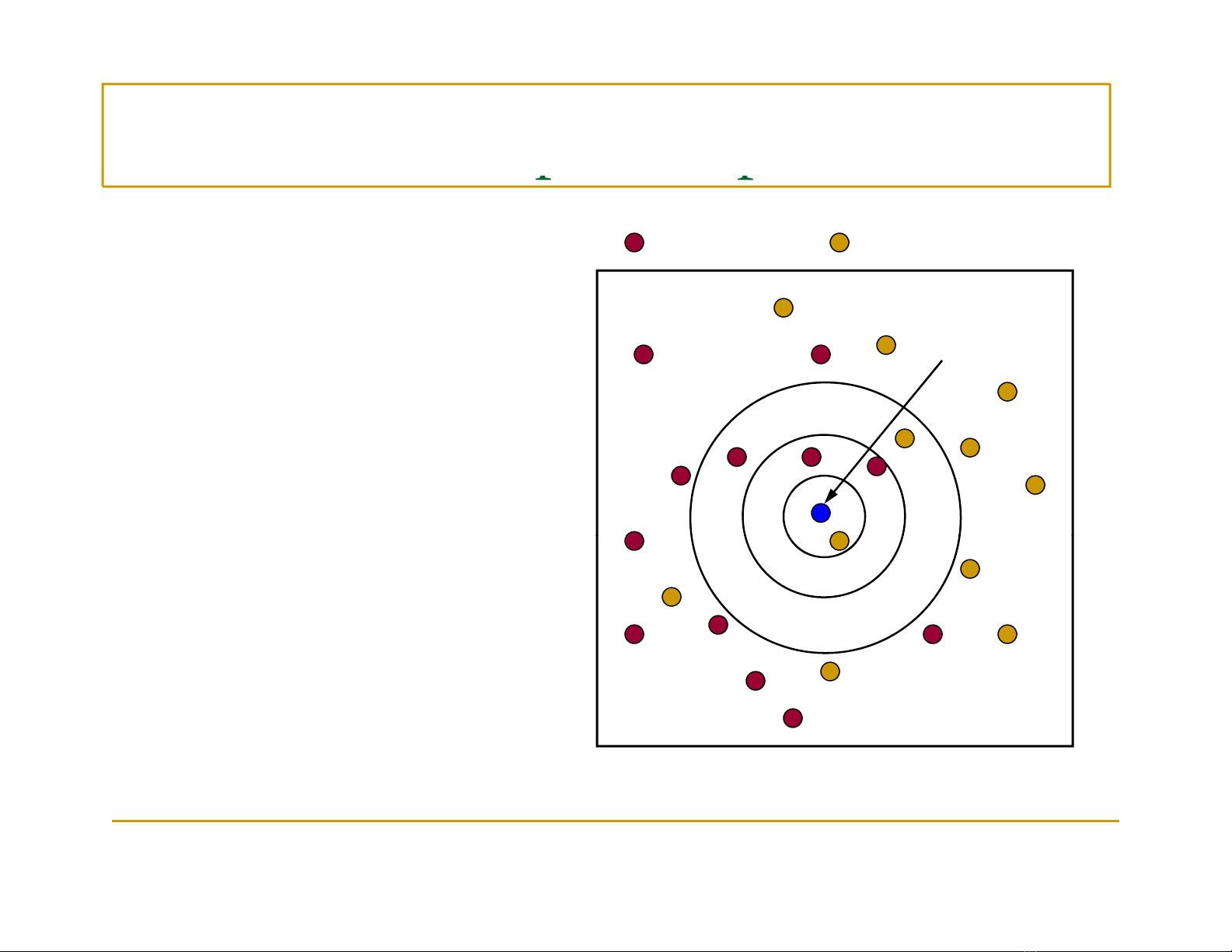
V
í dụbài toán
p
hân lớ
p
p
p
Lớp c1 Lớp c2
Xét 1 láng giềng gần
Ví dụ cần
phân lớp z
nhất
→Gán zvào lớpc2
Xét 3 láng giềng gần
nhất
→
Gán
z
vào
lớp
c1
→
Gán
z
vào
lớp
c1
Xét 5 láng giềng gần
nhất
nhất
→Gán zvào lớpc1
5
Học Máy – IT 4862



















![Hệ thống quản lý cửa hàng bán thức ăn nhanh: Bài tập lớn [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251112/nguyenhuan6724@gmail.com/135x160/54361762936114.jpg)
![Bộ câu hỏi trắc nghiệm Nhập môn Công nghệ phần mềm [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251111/nguyenhoangkhang07207@gmail.com/135x160/20831762916734.jpg)





