
Kiểu Bình Phương Latin
(LatinSQ)
–Yêu cầu:
•Khu thí nghiệm có 2 hướng biến thiên
• Hoặc chiều biến thiên khó xác định
được.
-Đặc điểm sau của kiểu LatinSQ
•Có số lần lập lại bằng với số nghiệm
thức
• Mỗi khối có đủ số nghiệm thức và
được phân phối ngẫu nhiên

• Các lô thí nghiệm được chia làm thành
r hàng và r cột.
• Mỗi hàng (row) hay mỗi cột (column)
đều có đủ các nghiệm thức và mỗi
nghiệm thức chỉ xuất hiện một lần.
– Ví dụ: một thí nghiệm khảo sát 5 giống lúa
mới đuợc bố trí theo kiểu LATINSQ. Hãy vẽ
sơ đồ bố trí
1
2
3
4
5
1
2
3
4
5
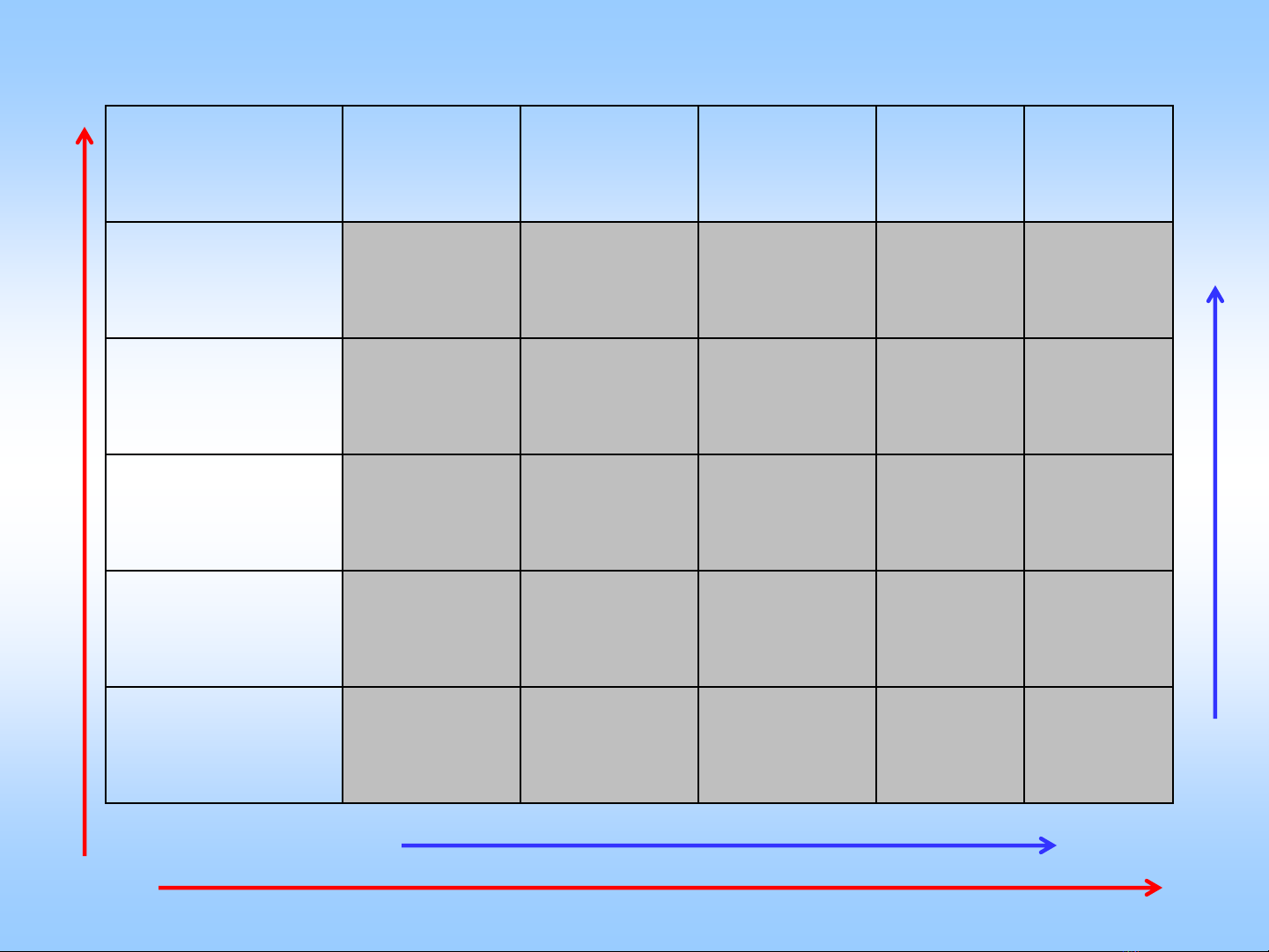
Chiều biến thiên
Chiều biến thiên
Cột
Hàng
Sơ đồ bố trí thí nghiệm
1
2
3
4
5
1
A
2
A
3
A
4
A
5
A
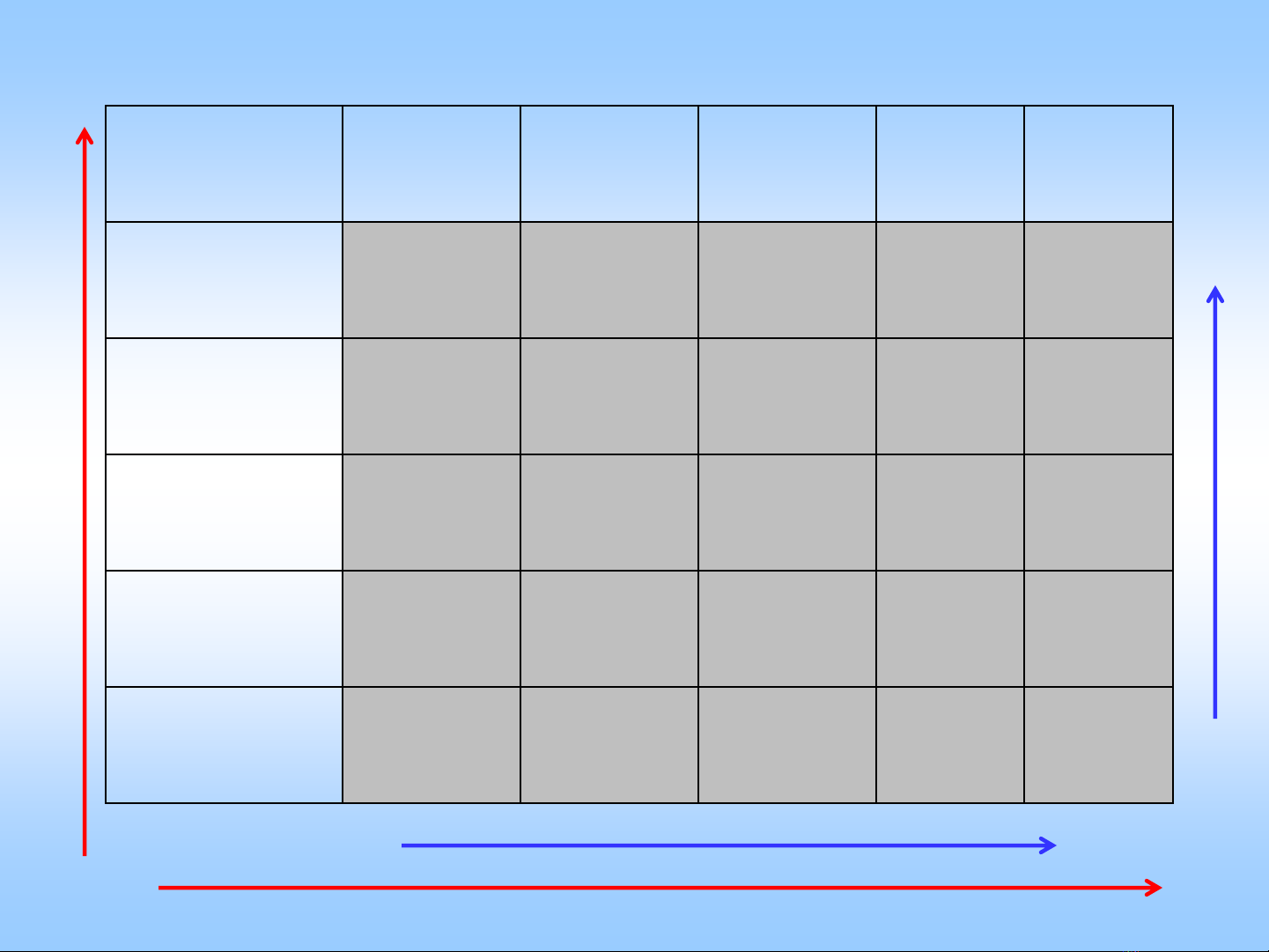
Chiều biến thiên
Chiều biến thiên
Cột
Hàng
Sơ đồ bố trí thí nghiệm
1
2
3
4
5
1
B
A
2
A
B
3
B
A
4
B
A
5
A
B
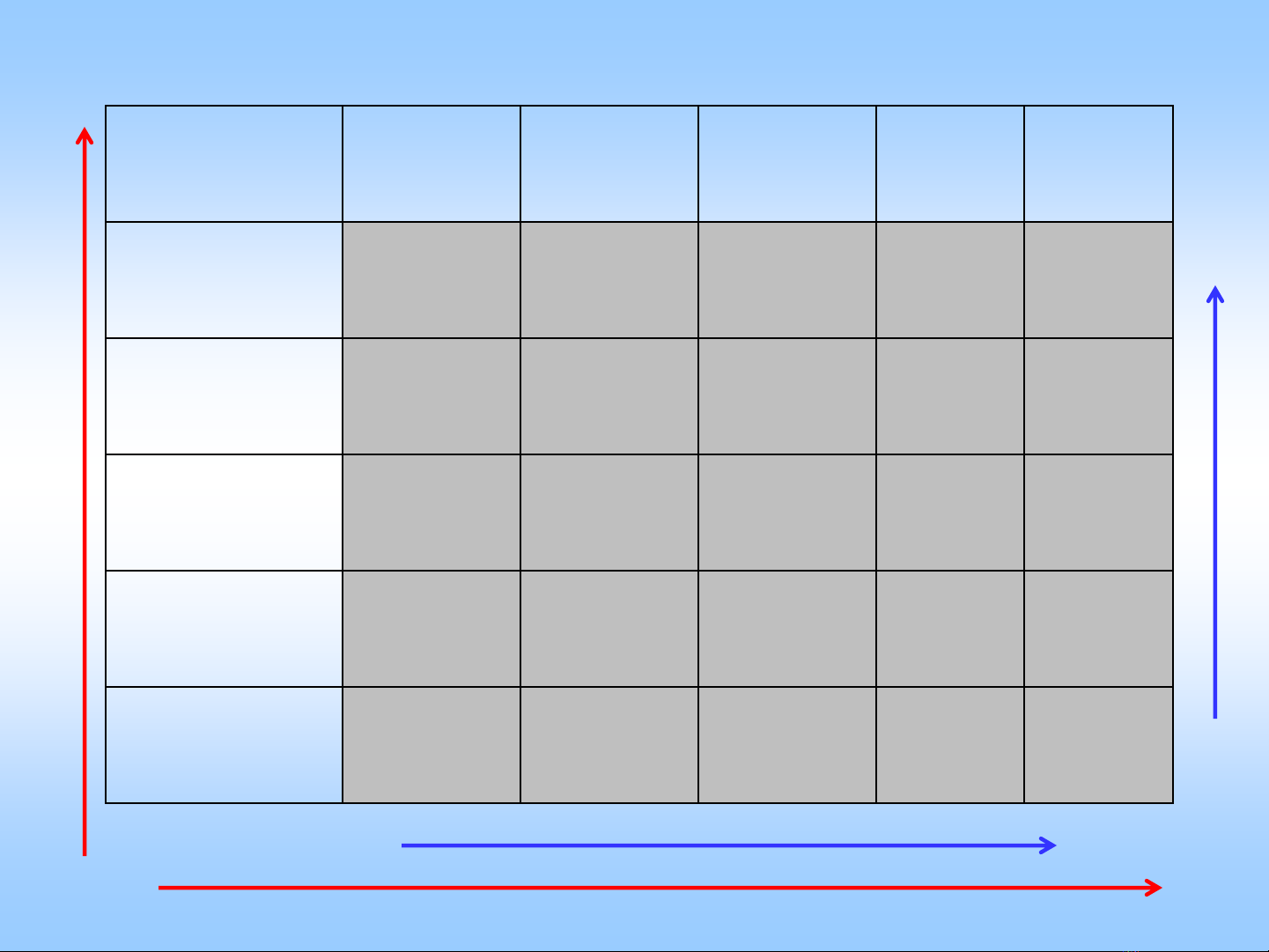
Chiều biến thiên
Chiều biến thiên
Cột
Hàng
Sơ đồ bố trí thí nghiệm


























