zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Kỹ Thuật - Công Nghệ

» Kiến trúc - Xây dựng

Bài giảng Kinh tế xây dựng: Chương 2.2 - Đặng Thế Gia

Chia sẻ: Trần Văn An | Ngày: | Loại File: PDF | Số trang:13

Báo xấu

48
lượt xem 2
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tiếp nội dung phần 2 sẽ cung cấp các kiến thức về Hệ số độ dốc số học P/G và A/G (Chuỗi thay đổi đều); Hệ số độ dốc P/G; Hệ số độ dốc A/G; Hệ số độ dốc số học F/G; Hệ số độ dốc hình học (Chuỗi thay đổi không đều); Tìm lãi suất và số năm;...Mời các bạn cùng tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Kinh tế xây dựng: Chương 2.2 - Đặng Thế Gia

11/18/2018 Chương 2: MÔN HỌC KINH TẾ XÂY DỰNG (KC269) Thời gian & Lãi suất Time & Interest GIÁO VIÊN PHỤ TRÁCH Phần 2 ĐẶNG THẾ GIA Bộ môn Kỹ Thuật Xây Dựng Khoa Công Nghệ, Trường Đại Học Cần Thơ Nội dung chương 1. Hệ số P/G & A/G 2. Gradient hình học 3. Tính lãi suất Hệ số độ dốc số học P/G & A/G 4. Tính thời đoạn (Chuỗi thay đổi đều) 5. Bảng tính Arithmetic Gradient Factors P/G & A/G Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ
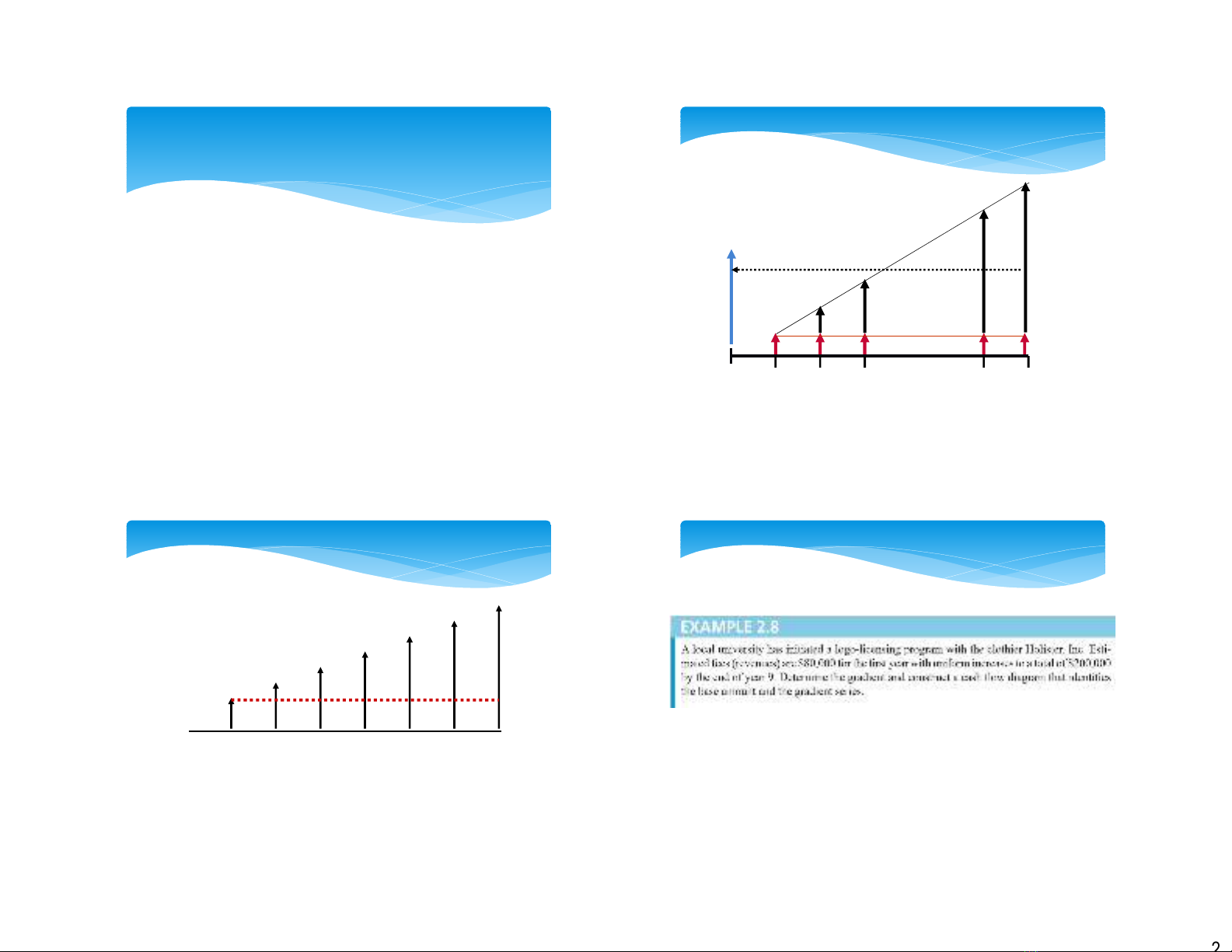
11/18/2018 Khái niệm A1+(n-1)G  Cấu hình dòng tiền A1+(n-2)G Tìm P, biết độ dốc G của dòng tiền Hệ số độ dốc P/G A1+2G A1+G Số tiền ban đầu = A1 0 1 2 3 n-1 n Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ CFi = A1 ± (i - 1)G Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Ví dụ Ví dụ $700 $600 $500 $400 $300 $200 $100 0 1 2 3 4 5 6 7 Độ dốc gồm hai thành phần: Số tiền ban đầu & lượng gia tang (gradient) 1. Số tiền ban đầu = $100 2. Số tiền gia tang (bên trên) = $100/thời đoạn Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ
11/18/2018 Ví dụ Ví dụ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Cấu thành của độ dốc Phân rã độ dốc (Gradient composition) (Gradient Decomposition) (n-2)G (n-1)G  (n-3)G Tìm P của chuỗi dốc Chúng ta đã biết, độ dốc số học gồm hai 2G 1G thành phần 0G Thành phần không đổi = A / thời gian 1. Số tiền ban đầu (Base amount) …….. 2. Thành phần độ dốc (Gradient component) 0 1 2 3 n-2 n-1 n Khi dòng tiền có độ dốc, hệ số P/G là độ dốc cấu thành duy nhất  Giá trị hiện tại là điểm cách một đơn vị thời gian về phía trái của nơi có giá trị độ dốc 0G  Áp dụng hệ số P/A đối với số tiền ban đầu  Để tính giá trị hiện tại của số tiền ban đầu, sử dụng hệ số P/A (đã biết)  PT = PA1 (base amount) + PG (gradient)  Để tính giá trị hiện tại của chuỗi độ dốc, sử dụng hệ số P/G (xem phía sau) Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ
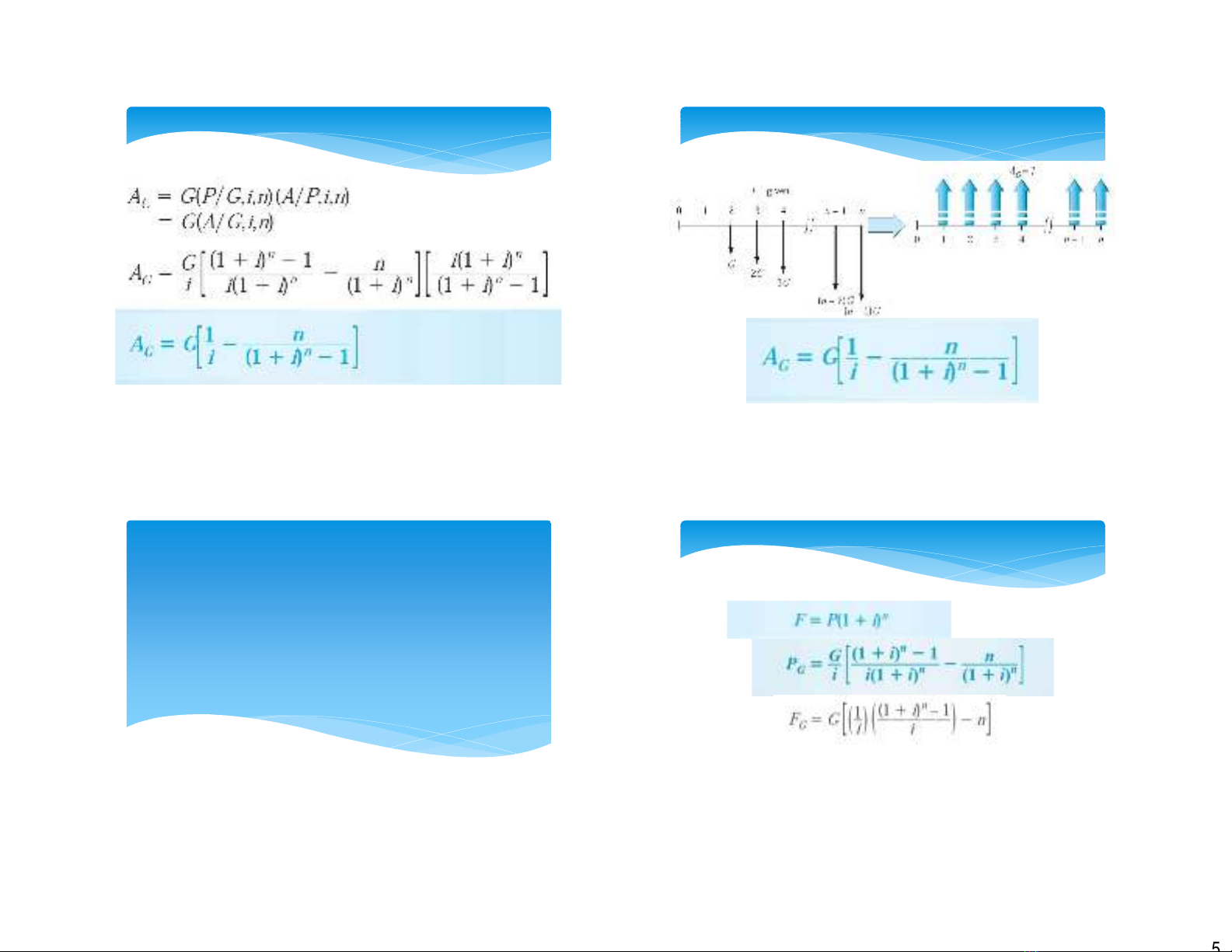
11/18/2018 Thành lập công thức Dạng bài toán Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Khái niệm AG = G(A/G,i,n) (n-1)G  Cấu hình dòng tiền (n-2)G Tìm AG, biết độ dốc G AG AG AG ... AG AG 2G Hệ số độ dốc A/G G A tương đương của chuỗi độ dốc 0 1 2 3 n-1 n CFi = (i - 1)G AT = A1 (base amount) + AG (gradient) Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ
11/18/2018 Thành lập công thức Dạng bài toán Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Thành lập công thức Hệ số độ dốc số học F/G Arithmetic Gradient Factor F/G Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ
11/18/2018 Ví dụ Ví dụ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Ví dụ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ
11/18/2018 Ví dụ Ví dụ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ $75 Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ
11/18/2018 Hệ số độ dốc hình học $75 (Chuỗi thay đổi không đều) Geometric Gradient Series Factor Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Khái niệm Chuỗi độ dốc hình học điển hình • Đôi khi các chi phí bảo quản, vận hành, nhân công,… A1(1+g)n-1 tăng/giảm theo một tỉ lệ nhất định, chẳng hạn 0.1%/tháng hay 3%/năm. • Độ dốc hình học (Geometric Gradient)  Chuỗi dung tiền bắt đầu từ giá trị A1  Tăng/giảm một tỉ lệ (lãi suất) không đổi (constant Cho biết A1, i%, và g% percentage) theo thời gian  Tỉ lệ/Lãi suất này được gọi là: A1(1+g)2 A1(1+g) A1 o Độ dốc hình học (Geometric Gradient) o Ký hiệu: .... 0 1 2 3 n-2 n-1 n g = tỉ lệ/lãi suất, tính bằng %, theo đó giá trị tương lai sẽ tăng/giảm theo mỗi đơn vị thời gian Yêu cầu: Tìm hệ số (P/A,g%,i%,n) dùng để chuyển đổi dòng tiền hàng năm trong tương lai về thời điểm hiện tại (t = 0) Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ
11/18/2018 Thành lập công thức Thành lập công thức  Trường hợp g ≠ i  Trường hợp g = i Nhân 2 vế cho (1+g)/(1+i) rồi trừ cho phương trình trên: Thay g = i vào phương trình trên: Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Dạng bài toán Các ghi chú Trường hợp g ≠ i Trường hợp g = i  1 g   n n A1 1      1 i   g  i Pg  Pg  A1  (1  i )  ig      Các lưu ý khi sử dụng hệ số (P/A,g%,i%,n)  A1 là giá trị khởi điểm  Bài toán này KHÔNG có số tiền ban đầu  Lượng tiền ở những năm (thời đoạn) kế tiếp được tình trực tiếp từ A1 Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ
11/18/2018 Ví dụ Ví dụ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Ví dụ Ví dụ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ
11/18/2018 Ví dụ Tìm lãi suất và số năm Determination of Unknown Interest Rate & Unknown Number of Years Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặt vấn đề Đặt vấn đề  Khi tất cả các giá trị dòng tiền được biết đến hoặc  Có vài cách để tìm i & n chưa biết, tùy thuộc vào đã được ước tính, giá trị i (interest rate or rate of bản chất của dòng tiền tệ và tùy thuộc vào phương return) hoặc giá trị n (số năm) thường là chưa biết. pháp tìm.  Ví dụ: Một công ty đầu tư vốn để phát triển một sản  Các trường hợp tìm i & n sẽ đơn giản khi chỉ liên phẩm mới. Sau vài năm, giá trị thu nhập ròng hàng quan đến giá trị hiện tại và giá trị tương lai (P & F). năm trên thị trường đã được biết, vấn đề đặt ra là cần xác định tỷ lệ lợi nhuận (rate of return) trên vốn  Các trường hợp tìm i & n sẽ phức tạp hơn khi liên đầu tư. quan đến A, G, và đặc biệt là g. Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ
11/18/2018 Ví dụ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Ví dụ Tóm tắt chương 2 • Các công thức và hệ số được thành lập và áp dụng trong chương này giúp xác định đương lượng (giá trị tương đương) của dòng tiền hiện tại (P), tương lai (F), chuỗi hàng năm (A), và có chuỗi có độ dốc (G); • Các công thức cho phép tính toán quy đổi qua lại các kiểu dòng tiền khác nhau; • Cho phép tính lãi suất (i) và thời gian (n); • Khả năng ứng dụng của các công thức và ký hiệu có ý nghĩa quan trọng cho các nghiên cứu kinh tế kỹ thuật. Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ Đặng Thế Gia, BM Kỹ Thuật Xây Dựng, Đại Học Cần Thơ
11/18/2018 XIN CẢM ƠN!

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.15: Bộ Đồ Án Tốt Nghiệp Chuyên Ngành Cơ Khí

65 tài liệu

2431 lượt tải

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.