http://www.ebook.edu.vn 14
−
−฀
−
−
−
−
Ch−¬ng 3. ChuyÓn ®æi ®iÖn tõ
Lµ chuyÓn ®æi trong ®ã ®¹i l−îng kh«ng ®iÖn (th−êng lµ c¸c di chuyÓn th¼ng hay gãc )
dÉn ®Õn thay ®æi ®iÖn c¶m, hç c¶m hoÆc xuÊt hiÖn søc ®iÖn ®éng c¶m øng ë cuén d©y.
http://www.ebook.edu.vn 15
Bµi 1. ChuyÓn ®æi ®iÖn c¶m
ChuyÓn ®æi ®iÖn c¶m lµ chuyÓn ®æi biÕn ®æi gi¸ trÞ ®¹i l−îng ®o thµnh trÞ sè ®iÖn c¶m
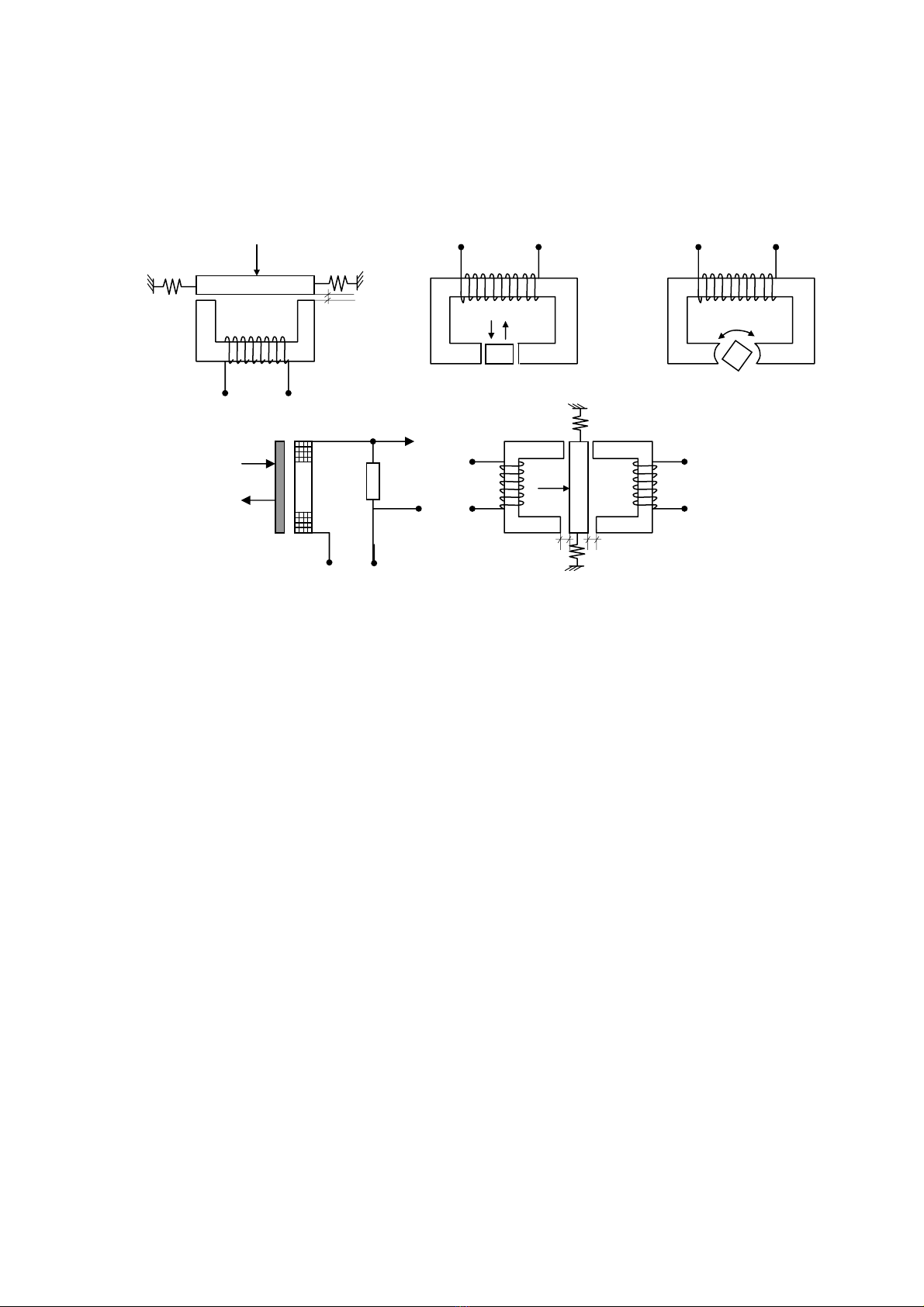
a. Mét sè lo¹i chuyÓn ®æi th−êng gÆp nh− sau:
H×nh 3.14 Mét sè chuyÓn ®æi ®iÖn c¶m th−êng gÆp
-H×nh a lµ chuyÓn ®æi ®¬n kh¸ phæ biÕn, d−íi t¸c dông cña ®¹i l−îng c¬ häc P vÝ
dô nh− lùc, ¸p xuÊt, sù di chuyÓn v.v sÏ lµm thay ®æi khe hë kh«ng khÝ δ nªn lµm thay
®æi tõ trë toµn bé m¹ch tõ. Nh− vËy sÏ lµm thay ®æi tæng trë Z còng nh− ®iÖn c¶m L cña
cuén d©y.
H×nh b, c d−íi t¸c dông cña ®¹i l−îng c¬ häc P sÏ lµm thay ®æi khe hë kh«ng khÝ δ.
ChuyÓn ®æi nµy th−êng dïng ®Ó ®o nh÷ng di chuyÓn tõ 5 ÷ 20mm hoÆc di chuyÓn gãc.
H×nh d lµ chuyÓn ®æi lµm thay ®æi dßng ®iÖn xo¸y, gåm mét cuén d©y kh«ng lâi
thÐp ®−îc m¾c vµo ®iÖn ¸p cã tÇn sè rÊt cao(cì vµi Mhz). Khi ta di chuyÓn tÊm kim lo¹i
hoÆc vßng d©y ng¾n m¹ch sÏ lµm thay ®æi tæn hao tõ trong cuén d©y, do vËy ®iÖn c¶m L
cña cuén d©y còng thay ®æi theo. H×nh a, b, c, d cßn gäi lµ chuyÓn ®æi ®iÖn tõ ®¬n.
H×nh e lµ chuyÓn ®æi lµm thay ®æi khe hë kh«ng khÝ kiÓu vi sai, gåm hai cuén d©y
gièng hÖt nhau. Khi chuyÓn ®æi ch−a lµm viÖc th×:
δ1 = δ2 =δ0, Z1 = Z2 =Z0
NÕu chuyÓn ®æi lµm viÖc th×: δ1 ≠ δ2, Z1 = Z0 ± ΔZ, Z2 = Z ± ΔZ
b. TÝnh n¨ng cña chuyÓn ®æi ®iÖn c¶m
NÕu ta bá qua tõ trë cña m¹ch tõ th×:
(a)
W W
P
(c) (b)
δ
R
U≈ (d) (e)
P
δ1 δ2
P
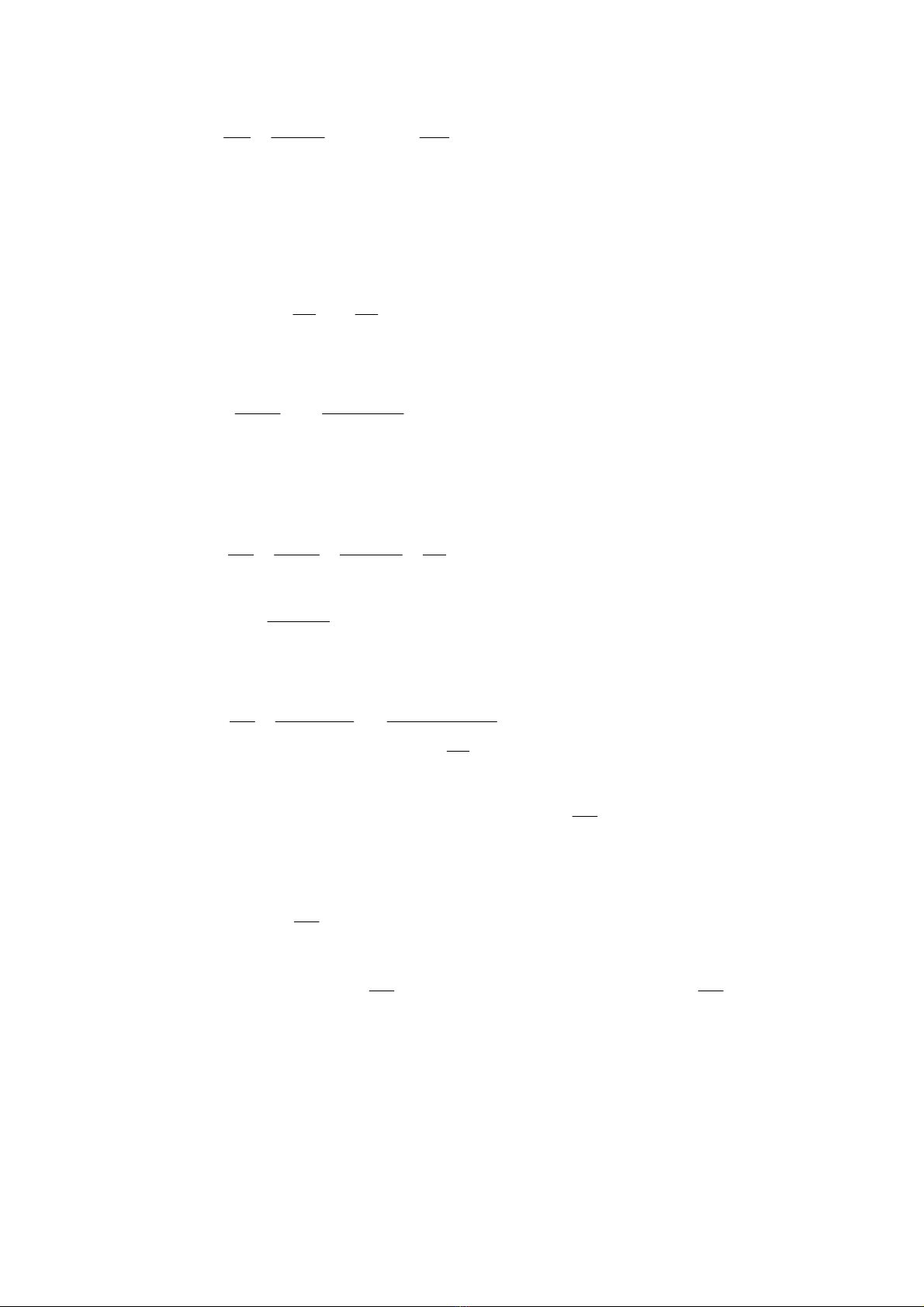
http://www.ebook.edu.vn 16
δ
µ
==
µ
Sw
R
w
L
2
0
2
, víi S
R
0
µ
δ
=
µ
w: lµ sè vßng d©y, µ0 = 4π.10-7 lµ hÖ sè dÉn tõ cña kh«ng khÝ, δ lµ chiÒu dµi khe hë
kh«ng khÝ, S tiÕt diÖn hiÖu dông cña khe hë kh«ng khÝ, Rµ lµ tõ trë cña khe hë kh«ng khÝ
VËy L phô thuéc vµo S vµ δ, sù biÕn thiªn cña L theo S vµ δ nh− sau:
Ta cã: δ
δ∂
∂
+
∂
∂
=d
L
dS
S
L
dL
víi l−îng thay ®æi h÷u h¹n Δδ vµ ΔS th×
δΔ
δΔ+δ
µ
−Δ
δ
µ
=Δ 2
0
0
2
0
0
2
0
)(
Sw
S
w
L
Trong ®ã S0, δ0 lµ gi¸ trÞ ban ®Çu cña S vµ δ khi chuyÓn ®æi ch−a lµm viÖc
+§é nh¹y cña chuyÓn ®æi khi tiÕt diÖn thay ®æi (δ = δ0 =const)
Ss = const
S
L
S
Sww
L
0
0
00
00
2
0
0
2
==
δ
µ
=
δ
µ
=
δΔ
Δ
Víi L0 =
0
0
2
0Sw
δ
µ lµ gi¸ trÞ ®iÖn c¶m ban ®Çu cña chuyÓn ®æi
+ §é nh¹y cña chuyÓn ®æi khi δ thay ®æi lµ (S = S0 =const):
()
2
0
0
0
2
0
0
2
0
1
LSw
L
S
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
δ
δΔ
+δ
−=
δΔ+δ
µ
=
δΔ
Δ
=
δ
Ta thÊy ®é nh¹y cña chuyÓn ®æi phô thuéc vµo
0
δ
δΔ
NhËn xÐt: §é nh¹y cña chuyÓn ®æi khi S thay ®æi b»ng h»ng sè, cßn khi δ thay ®æi
th× phô thuéc vµo
0
δ
δΔ , vËy quan hÖ gi÷a L=f(δ) lµ phi tuyÕn. Thùc tÕ cho thÊy quan hÖ
L = f(δ) lµ tuyÕn tÝnh khi
0
δ
δΔ ≤ 0.2 ®èi víi chuyÓn ®æi ®¬n, vµ
0
δ
δΔ ≤ 0.4 ®èi víi
chuyÓn ®æi vi sai.
http://www.ebook.edu.vn 17
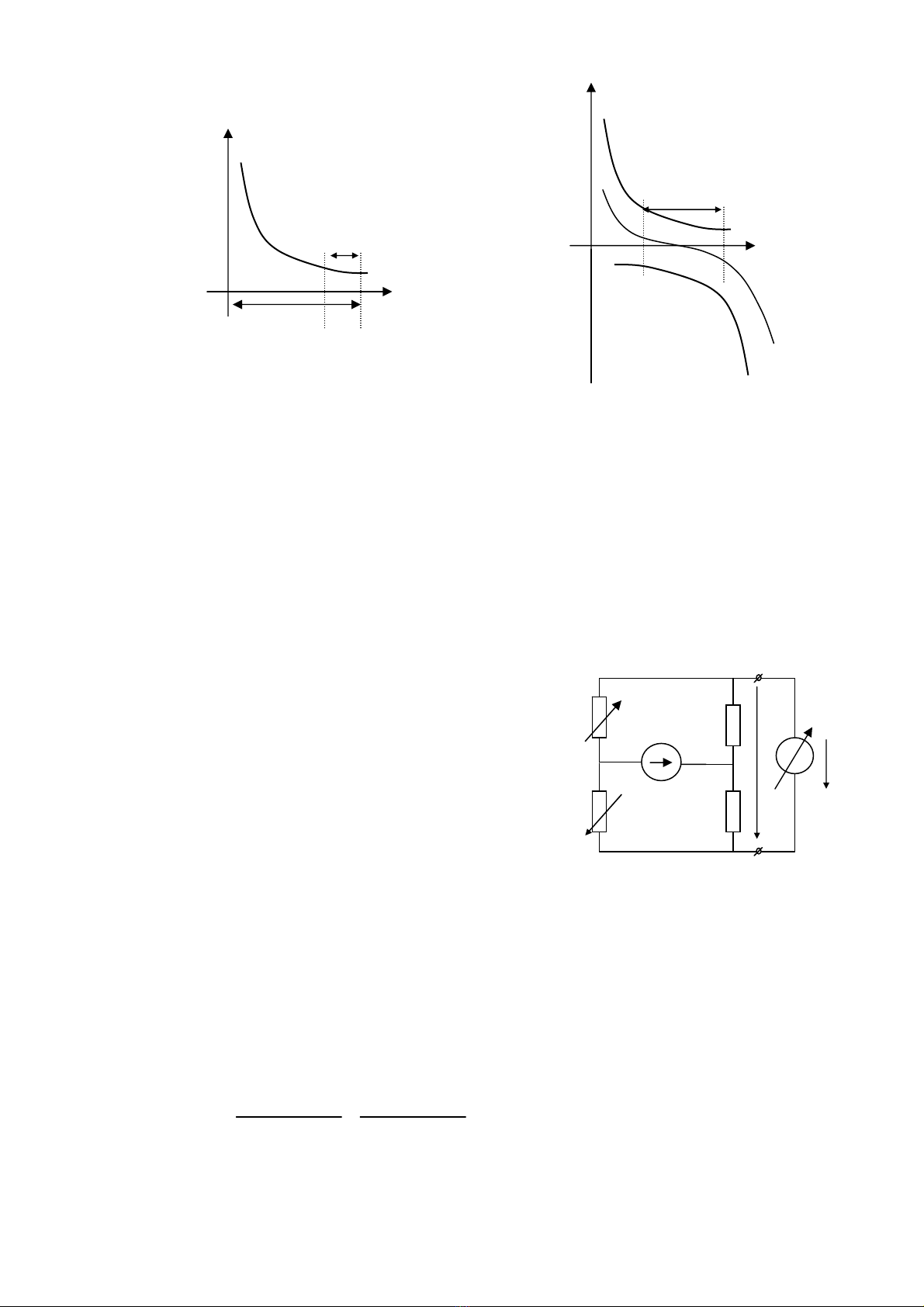
H×nh 3.15 Quan hÖ gi÷a ®iÖn c¶m vµ sù biÕn thiªn
δ
cña chuyÓn ®æi ®iÖn c¶m
c. M¹ch ®o cña chuyÓn ®æi
Sù biÕn thiªn ®iÖn c¶m sÏ lµm biÕn thiªn trë kh¸ng trong toµn m¹ch. M¹ch ®o cã
nhiÖm vô biÕn ®æi tiÕp tÝn hiÖu thµnh ®¹i l−îng ®iÖn ®ñ lín ®Ó cã thÓ ph¸t ra c¸c tÝn hiÖu
khèng chÕ mét c¸ch ch¾c ch¾n, biÕn thiªn ®iÖn c¶m trong m¹ch cã thÓ dÉn ®Õn biÕn
thiªn vÒ biªn ®é hoÆc pha hoÆc tÇn sè cña ®iÖn ¸p hay dßng ®iÖn ®Çu ra. M¹ch ®o cã tªn
t−¬ng øng lµ m¹ch ®iÒu biªn, ®iÒu pha hoÆc ®iÒu tÇn. Ta sÏ nghiªn cøu m¹ch th«ng dông
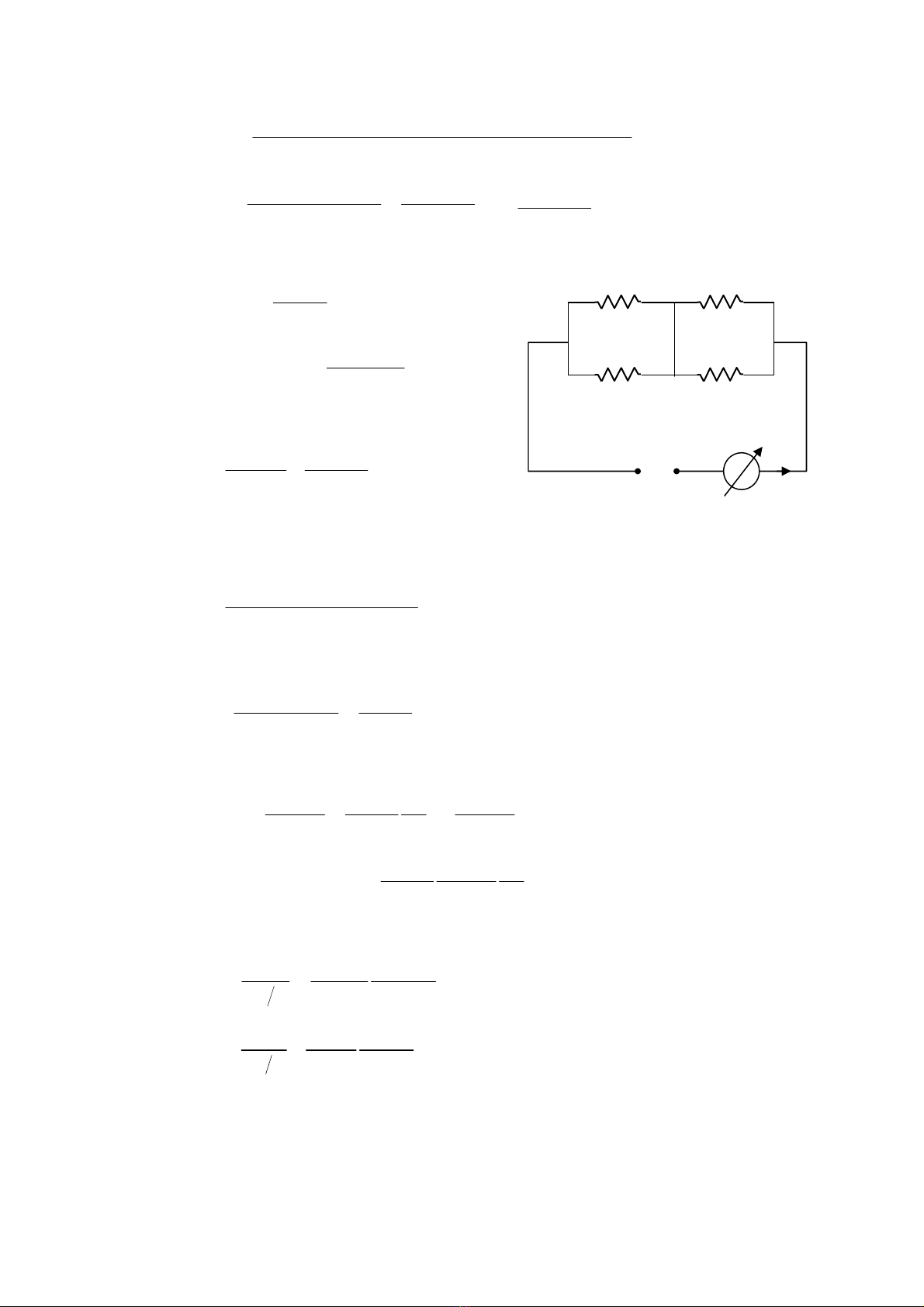
lµ m¹ch ®iÒu biªn. M¹ch nµy th−êng lµ m¹ch cÇu vi sai nh− sau:
Z1, Z2 lµ trë kh¸ng cña chuyÓn ®æi vi sai.
Zb lµ trë kh¸ng phèi hîp víi Z1 vµ Z2
Z0 trë kh¸ng cña dông cô ®o.
U nguån cung cÊp,
+Khi trôc ®o n»m ë vÞ trÝ c©n b»ng
δ1 = δ2 = δ0, Z1 = Z2 = Z
CÇu c©n b»ng vµ Ura = 0
+Khi trôc ®o lÖch khái vÞ trÝ c©n b»ng tøc lµ δ1 vµ δ2 biÕn thiªn ng−îc nhau 1 l−îng
lµ Δδ, khi ®ã Z1 vµ Z2 còng biÕn thiªn mét l−îng lµ ΔZ. Ta gi¶ sö
Z1 = Z + ΔZ, Z2 = Z - ΔZ
Ta ®i t×m quan hÖ gi÷a sù biÕn thiªn cña ®iÖn ¸p Ur theo sù biÕn thiªn ΔZ nh− sau:
+ Gäi Uh lµ ®iÖn ¸p khi hë m¹ch ®o ( Z0 = ∞)
b
b
b
b
hZ)ZZ(
EZ
Z)ZZ(
EZ
U+Δ+
−
+Δ−
=
δ
δ0
Δ
δ
L
L = f(δ)
ChuyÓn ®æi ®¬n
δ
L1-L2=f3(δ)
Δδ
L
L1= f1(δ)
ChuyÓn ®æi vi sai
L2 = f2(δ)
Ur
Z1
Z2
Zb
Zb
E Z0
Uh
H×nh 3.16 M¹ch cÇu vi sai chuyÓn ®æi ®iÖn c¶m
http://www.ebook.edu.vn 18
()()
22
b
2
bbb
2
bbb
ZZZ
EZZEZZEZEZZEZZEZ
Δ−+
+Δ−−+Δ+
=
=
()()()
2
b
b
22
b
b
ZZ
ZEZ2
ZZZ
ZEZ2
+
Δ
≈
Δ−+
Δ =
()
2
b
b
ZZ
ZEZ2
+
Δ
+ Gäi Uz lµ ®iÖn ¸p r¬i trªn c¸c phÇn tö cña chuyÓn ®æi vi sai khi chuyÓn ®æi ch−a
lµm viÖc: Uz =
b
ZZ
EZ
+
VËy ta cã Uh =
()
ZZZ
ZUZ2
b
zb
+
Δ
+ Trë kh¸ng trong cña cÇu
Zi =
b2
b2
b1
b1
ZZ
ZZ
ZZ
ZZ
+
+
+
Thay Z1 = Z + ΔZ, Z2 = Z - ΔZ, quy ®ång mÉu sè vµ rót gän ta ®−îc
Zi =
()
2
2
b
2
b
2
bb
2
ZZZ
Z
Z2ZZ2ZZ2
Δ−+
Δ
−+
V× ΔZ kh¸ nhá cho nªn ta cã thÓ bá qua ΔZ2
Zi ≈
()
()
b
b
2
b
bb
ZZ
ZZ2
ZZ
ZZZZ2
+
=
+
+
+Quan hÖ gi÷a dßng ®iÖn I0 vµ ®iÖn ¸p Ura theo sù biÕn thiªn ΔZ lµ:
VËy I0 =
0i
z
b
b
0i
0
ZZ
1
U
Z
Z
ZZ
Z2
ZZ
U
+
Δ
+
=
+
Hay Z
0i
0
b
b
00ra
'
0U
Z
Z
ZZ
Z
ZZ
Z2
ZIUU Δ
++
===
+ §é nh¹y vÒ dßng vµ ¸p cña cÇu:
z
0i0
b0
SI U
ZZ
1
ZZ
Z2
ZZ
I
K++
=
Δ
=
'
00
00
2.
b
SU z o SI
i
UZZ
KUZK
ZZ Z Z Z Z
== =
Δ++
B»ng c¸ch tÝnh t−¬ng tù ta cã thÓ tÝnh ®−îc ®é nh¹y dßng vµ ¸p cña nhiÒu m¹ch
chuyÓn ®æi
d. ¦u nh−îc ®iÓm vµ øng dông
Z0
Uh
I0
Z1
Z2
Zb Zb
H×nh 3.17 M¹ch thay thÕ cña chuyÓn ®æi vi sai