
LOGO
Chương
Chương 2
2
GI
GIÁ
ÁTR
TRỊ
ỊTHEO TH
THEO THỜ
ỜI GIAN
I GIAN
C
CỦ
ỦA TI
A TIỀ
ỀN T
N TỆ
Ệ
Gv: ThS.HàngLêCẩmPhương
KhoaQuảnLýCôngNghiệp
Nộidung
CÔNG THỨC GIÁTRỊ TƯƠNG ĐƯƠNG CỦA DÒNG TIỀN
LÃI SUẤT
MỘT SỐKHÁI NIỆM
VÍDỤ
1. MỘT SỐKHÁI NIỆM
vLãi tức (Interest): là lượng tiền tăng lên từsốvốn
gốc đem đầu tư đến sốvốn tích lũy cuối cùng.
Lãi tức = Tổng vốn tích lũy –Vốn đầu tư ban đầu
vLãi suất (Interest Rate): biểu thịphần trăm của lãi
tức đối với sốvốn ban đầu trên 1 đơn vịthời gian.
Lãisuất= (Tiềnlãi/ Vốngốc) x 100%
1. MỘT SỐKHÁI NIỆM
vLãi tức đơn (Single Interest): chỉtính theo vốn gốc ban đầu màkhông
xét đến phần lãi tức tích lũy, phát sinh do tiền lãi của những thời đoạn
trước.
Lãi tức đơn = Vốn đầu tư ban đầu x Lãi suất đơn x Sốthời đoạn
i = P.S.N
Trong đóP : sốvốn cho vay (đầu tư)
S : lãi suất đơn
N : sốthời đoạn trước khi thanh toán (rút vốn)
vLãi tức ghép (Compound Interest): lãi tức tại mỗi thời đoạn được tính
theo vốn gốc vàtổng tiền lãi tích lũy được trong các thời đoạn trước đó
=> với lãi suất ghép lài%, sốthời đoạn làN, P làvốn gốc:
Tổng vốn lẫn lãi sau N thời đoạn là: P(1+i)N
CuuDuongThanCong.com https://fb.com/tailieudientucntt
2. LÃI SUẤT
LÃI SUẤT
DANH NGHĨA
LÃI SUẤT
LÃI SUẤT
THỰC
2. LÃI SUẤT
Lãisuấtdanhnghĩavàlãisuấtthực
Cáchphânbiệtlãisuấtdanhnghĩavàlãisuấtthực:
vKhi thời đoạn phát biểu lãi = thời đoạn ghép lãi
⇒lãi suất thực.
vKhi thời đoạn phát biểu lãi ≠thời đoạn ghép lãi
⇒lãi suất Danh nghĩa
vLãi suất phát biểu không cóxác định thời đoạn ghép lãi
lãi suất thực
vLãi suất thực hoặc danh nghĩa được ghi kèm theo mức lãi
suất phát biểu
2. LÃI SUẤT
Tínhlãisuấtthực:
vChuyển lãi suất thực theo những thời đoạn khác nhau
i2= (1+i1)m–1
Trong đó,
i1: lãi suất thực cóthời đoạn ngắn(Vd: tháng)
i2: lãi suất thực cóthời đoạn dài hơn (VD: năm)
m:sốthời đoạn ngắn trong thời đoạn dài (Vd: m = 12)
Vídụ: cho lãi suất 12%/ năm, ghép lãi năm. Hãy tính lãi
suất thực sau 5 năm?
i5= (1+ 0.12)5–1 = 0.7623
2. LÃI SUẤT
vChuyểntừlãisuấtdanhnghĩasang lãisuấtthực
Tính lãi suất danh nghĩa cho thời đoạn bằng thời
đoạn ghép lãi
Khi thời đoạn của lãi suất danh nghĩa bằng thời đoạn
ghép lãi thìlãi suất danh nghĩa đócũng chính làlãi
suất thực.
Vídụ: Lãi suất 12% năm, ghép lãi theo quý
3%/ quýcũnglàlãisuấtthựctheoquý.
CuuDuongThanCong.com https://fb.com/tailieudientucntt

2. LÃI SUẤT
vTínhlãisuấtthựctrong1 thờikỳtínhtoántheolãisuất
danhnghĩa
i = (1 + r/m1)m2 –1
Trong đó,
i : lãi suất thực trong 1 thời đoạn tính toán
r : lãi suất danh nghĩa trong thời đoạn phát biểu
m1: sốthời đoạn ghép lãi trong 1 thời đoạn phát biểu
m2: sốthời đoạn ghép lãi trong 1 thời đoạn tính toán
Vídụ: Lãi suất 12%/ năm, ghép lãi theo quý, tính lãi suất
thực của 1 năm, nửa năm?
Lãi suất thực của 1 năm: i = (1 + 12%/4)4–1 = 12,55%
Lãi suất thực của nửa năm: i = (1 + 12%/4)2–1 = 6,09%
3. BIỂU ĐỒ DÒNG TIỀN TỆ
a. Khái niệm vềbiểu đồ dòng tiền tệ
vDòng tiềntệcủadựán(Cash Flow –CF): cáckhoảnthuvàchi
vQuy ước, các khoản thu/ chi đều xảy ra tại cuối mỗi thời đoạn.
Ởmỗi thời đoạn: Dòng tiền tệròng = Khoản thu –Khoản chi
P
0
A1
A2
F1
F2
2 3 4 5
1 6 7 8 9 10 …n
i%
3. BIỂU ĐỒ DÒNG TIỀN TỆ
b. Các ký hiệu trên biểu đồ dòng tiền tệ
↑: dòng tiền tệ dương, thu nhập
↓: dòngtiềntệâm, chi phí
P (Present Value): giátrịhiện tại, quy ước tại 1 điểm mốc nào đó
(thường ởcuối năm 0, đầu năm 1 của dựán)
F (Future): giátrị tương lai tại 1 điểm mốc quy ước nào đó(khác
điểm 0).
A (Annual/Uniform value): chuỗi các dòng tiền tệcógiátrịbằng
nhau, đặt cuối vàliên tục theo một sốthời đoạn
n (Number): sốthời đoạn(Vídụ: năm, tháng, quý, …)
i% (Interest): lãisuấthay suấtchiếttính (Discount Rate).
3. BIỂU ĐỒ DÒNG TIỀN TỆ
c. Tínhchất
vTính cộng: các dòng tiền tệtại cùng một thời điểm
cóthểcộng/ trừvới nhau để códòng tiền tệ“tương
đương”tại thời điểm đó.
CuuDuongThanCong.com https://fb.com/tailieudientucntt

3. BIỂU ĐỒ DÒNG TIỀN TỆ
d. Các công thức tính giátrị tương đương cho các
dòng tiền tệ đơn vàtheo thời gian
vDòng tiền tệ đơn
Cho P tìmF
F = P(F/ P, i%, n)
Hệsố–Giátrị–Lũy tích đơn: (F/P, i%, n) = (1 + i)n
Cho F tìmP
P = F(P/ F, i%, n)
Hệsố–Giátrị–Hiện tại đơn: (P/F, i%, n) = 1/(1 + i)n
P
0
F
2 3 4 5
1 6 7 8 9 10 …n
i%
3. BIỂU ĐỒ DÒNG TIỀN TỆ
vDòng tiền tệphân phối đều
Cho A tìmF
F = A (F/A, i%, n)
Cho F tìmA
A = F (A/F, i%, n)
Cho A tìmP
P = A (P/A, i%, n)
Cho P tìmA
A = P (A/P, i%, n)
PF
0 1 2 3 4 5n
A
i%
Lưu ý: Với các biểu thức trên:
•GiátrịP phải đặt trước giátrị
đầu tiên của chuỗi A 1 thời
đoạn.
•GiátrịF phải đặt trùng với giátrị
cuối cùng của chuỗi A.
3. BIỂU ĐỒ DÒNG TIỀN TỆ
vDòng tiền tệliên tục đều vô hạn
Cho P t ìm A
A = P*i%
Cho A t ìm P
P = A/ i%
P
0 1 2 3 4 5n
A
∞
i%
3. BIỂU ĐỒ DÒNG TIỀN TỆ
vCác vídụ
Vídụ(Cho P tìm F): 1 người gởi tiết kiệm 600.000Đ, sau đó2
quý gởi thêm 300.000Đ, sau 5 quý gởi thêm 400.000Đ. Vậy
sau 10 quý, anh ta sẽ được tổng cộng bao nhiêu tiền nếu lãi
suất là5% quý?
Giải
0
F = ?
5Quyù
600.000 Ñ
210
3
300.000 Ñ 400.000 Ñ
CuuDuongThanCong.com https://fb.com/tailieudientucntt
3. BIỂU ĐỒ DÒNG TIỀN TỆ
Vídụ: 1 người vay 50 triệu Đ để mua tài sản vàsẽtrảnợ theo
phương thức: trả đều đặn 15 lần theo từng quý, kểtừcuối quý
thứ3. Lãi suất theo quý là5%. Hỏi giátrị1 lần trảlàbao nhiêu?
Giải
F2= P( F/P, 5% , 2) = 50.000.000(1,1025) = 55.125.00 0
A = P2( A/P, 5% , 15) = 55.125.000(0,0963)= 5.308.537,5
P = 50 trieäu Ñ
0
A = ?
2 3 4 5
1 14
i = 5%
15 16 17
F2= P2
3. BIỂU ĐỒ DÒNG TIỀN TỆ
e. Công thức tính giátrị tương đương cho các
dòng tiền tệphân bố không đều
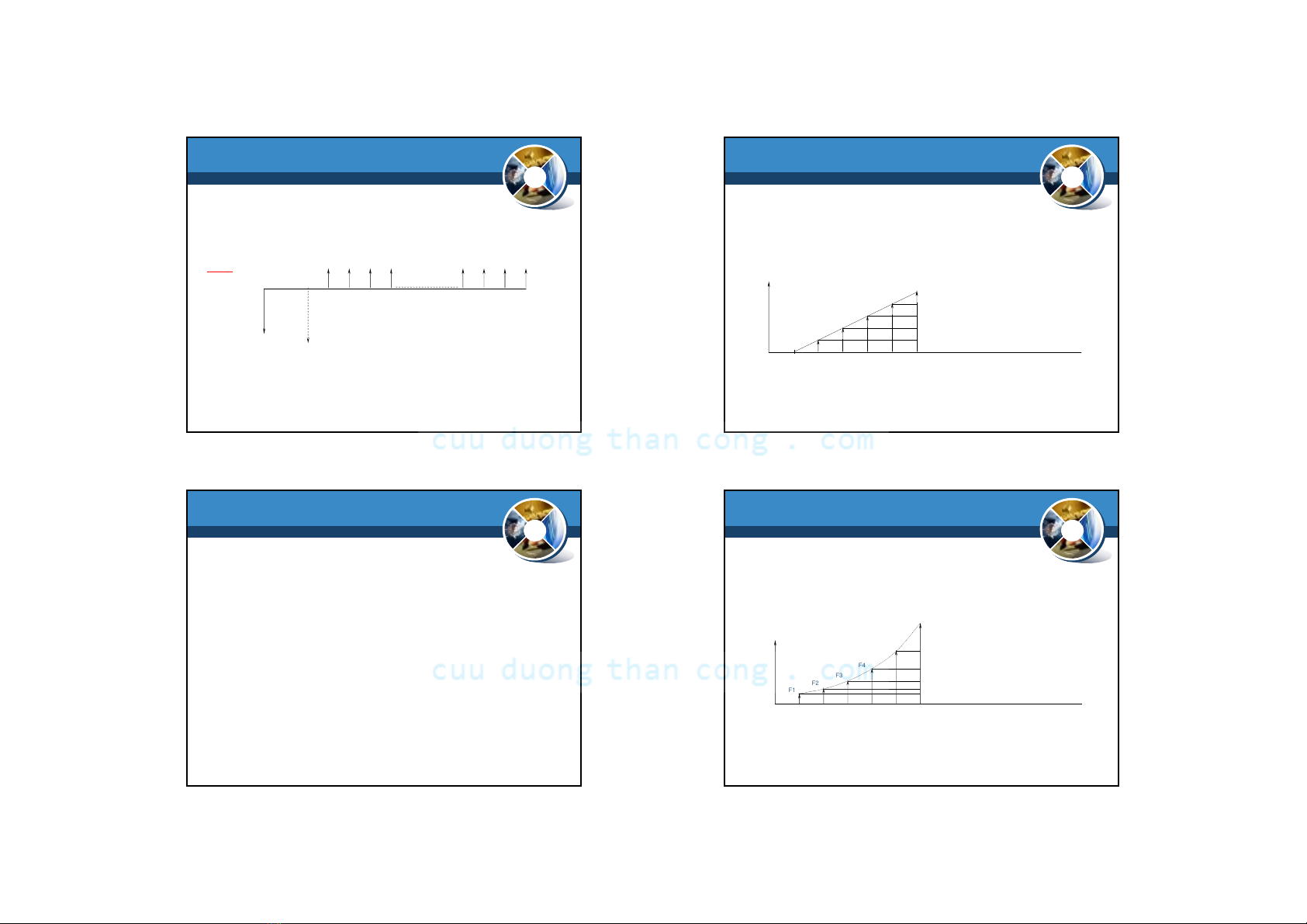
vDòng tiền tệ Gradient đều
P
023 4 5
1 6 7 8 9 10 …n
i%
11
G
G
G
G
G
1G
2G
3G
4G
5G
Hình: Bieåu ñoàdoøng tieàn teächuoãi Gradient ñeàu
3. BIỂU ĐỒ DÒNG TIỀN TỆ
vDòng tiền tệ Gradient đều
Ghi chú: GiátrịCF ởthời đoạn sau sẽlớn hơn (hoặc nhỏ hơn)giátrị
CF của thời đoạn trước 1 khoảng bằng nhau vàbằng G. Giátrị G đầu
tiên ởcuối thời đoạn 2. Khi đó, chuỗi dòng tiền tệ được gọi là Chuỗi
Gradient đều dương (hoặc đều âm).
Cho G tìm F
F = G (F/G, i%, n)
Cho G tìm P
P = G (P/G, i%, n)
Cho G tìm A
A = G (A/G, i%, n)
3. BIỂU ĐỒ DÒNG TIỀN TỆ
e. Công thức tính giátrị tương đương cho các
dòng tiền tệphân bố không đều(tt)
vDòng t iền t ệhình h ọc
P
02 3 4 51 6 7 8 9 10 …n
I%
11
F2 = F1 x (1+j%)
F1
F2
F3
F4
F5
F1
F6
F3 = F2 x (1+j%)
F4 = F3 x (1+j%)
F5 = F4 x (1+j%)
F6 = F5 x (1+j%)
Hình: Bieåu ñoàchuoãi doøng tieàn teähình hoïc
CuuDuongThanCong.com https://fb.com/tailieudientucntt


























