Next
Néi dung
Back
Bµi gi¶ng m¸y ®iÖn
Next
Néi dung
Back
Bµi gi¶ng m¸y ®iÖn
PhÇn 1: M¸y ®iÖn mét chiÒu
PhÇn 2: M¸y biÕn ¸p
PhÇn më ®Çu
Bµi gi¶ng m¸y ®iÖn
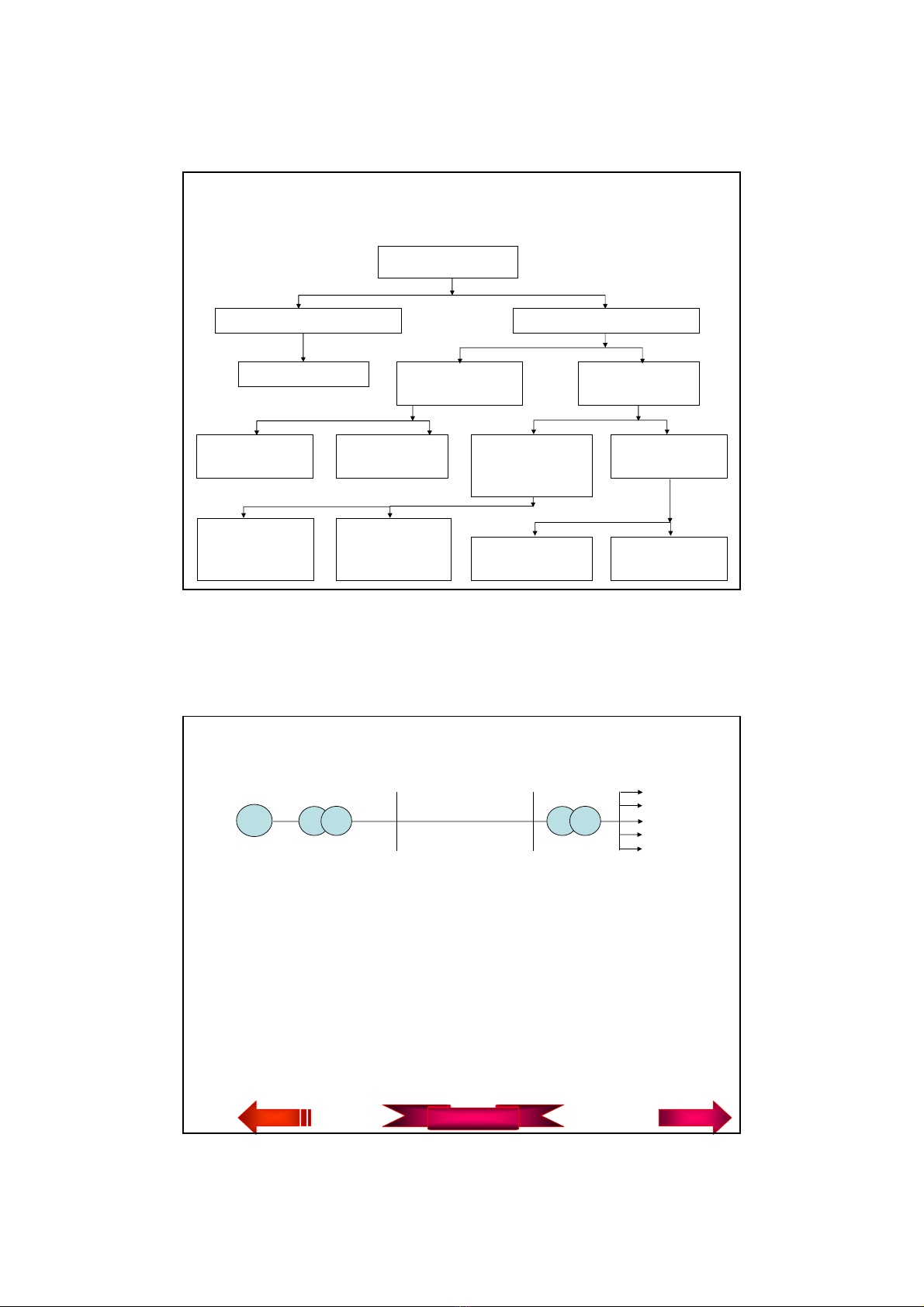
M¸y ®iÖn
M¸y ®iÖn tÜnh M¸y ®iÖn quay
M¸y biÕn ¸p M¸y ®iÖn
mét chiÒu M¸y ®iÖn
xoay chiÒu
®éng c¬
mét chiÒu M¸y ph¸t
mét chiÒu M¸y ®iÖn
kh«ng
®ång bé
M¸y ®iÖn
®ång bé
M¸y ph¸t
kh«ng
®ång bé
®éng c¬
kh«ng
®ång bé ®éng c¬
®ång bé M¸y ph¸t
®ång bé
Next
Néi dung
Back
Bµi gi¶ng m¸y ®iÖn
MF
Hé
tiªu
thô
MBA MBA
1. Vai trß cña c¸c lo¹i m¸y ®iÖn trong nÒn kinh tÕ quèc d©n:
2. Kh¸i niÖm, ph©n lo¹i vµ ph−¬ng ph¸p nghiªn cøu m¸y ®iÖn:
a, §¹i c−¬ng vÒ m¸y ®iÖn:
- Nguyªn lý lµm viÖc cña m¸y ®iÖn dùa trªn c¬ së cña ®Þnh luËt c¶m
øng ®iÖn tõ. Sù biÕn ®æi n¨ng l−îng trong m¸y ®iÖn ®−îc thùc hiÖn
th«ng qua tõ tr−êng trong nã. §Ó t¹o ®−îc nh÷ng tõ tr−êng m¹nh vµ
tËp trung, ng−êi ta dïng vËt liÖu s¾t tõ lµm m¹ch tõ.
ë m¸y biÕn ¸p m¹ch tõ lµ mét lâi thÐp ®øng yªn. Cßn trong c¸c
m¸y ®iÖn quay, m¹ch tõ gåm hai lâi thÐp ®ång trôc: mét quay, mét
®øng yªn vµ c¸ch nhau b»ng mét khe hë.
b, Ph−¬ng ph¸p nghiªn cøu m¸y ®iÖn:
Next
Néi dung
Back
Bµi gi¶ng m¸y ®iÖn
3. S¬ l−îc vÒ vËt liÖu chÕ t¹o m¸y ®iÖn:
Gåm cã vËt liÖu t¸c dông, vËt liÖu kÕt cÊu vµ vËt liÖu c¸ch ®iÖn.
VËt liÖu t¸c dông: bao gåm vËt liÖu dÉn ®iÖn vµ dÉn tõ dïng ®Ó chÕ
t¹o d©y quÊn vµ lâi s¾t.
VËt liÖu c¸ch ®iÖn: dïng ®Ó c¸ch ®iÖn c¸c bé phËn dÉn ®iÖn víi c¸c
bé phËn kh¸c cña m¸y vµ c¸ch ®iÖn c¸c l¸ thÐp cña lâi s¾t.
VËt liÖu kÕt cÊu: chÕ t¹o c¸c chi tiÕt m¸y vµ c¸c bé phËn chÞu lùc c¬
giíi nh− trôc, vá m¸y, khung m¸y.
S¬ l−îc ®Æc tÝnh cña vËt liÖu dÉn tõ, dÉn ®iÖn vµ c¸ch ®iÖn dïng
trong chÕ t¹o m¸y ®iÖn.
a, VËt liÖu dÉn tõ:
b, VËt liÖu dÉn ®iÖn:
c, VËt liÖu c¸ch ®iÖn:
CÊp c¸ch ®iÖn Y A E B F H C
NhiÖt ®é (
0
C) 90 105 120 130 155 180 >180
PhÇn 1: M¸y ®iÖn mét chiÒu
Ch−¬ng 1 : Nguyªn lý lµm viÖc - kÕt cÊu c¬ b¶n
Ch−¬ng 2 : D©y quÊn M¸y ®iÖn mét chiÒu
Ch−¬ng 3 : C¸c quan hÖ ®iÖn tõ trong m¸y
Ch−¬ng 4 : Tõ tr−êng trong m¸y ®iÖn mét chiÒu
Ch−¬ng 5 : §æi chiÒu
Ch−¬ng 6 : M¸y ph¸t ®iÖn mét chiÒu
Ch−¬ng 7 : §éng c¬ mét chiÒu
Ch−¬ng 8 : M¸y ®iÖn mét chiÒu ®Æc biÖt
Next
Néi dung
Back
Bµi gi¶ng m¸y ®iÖn
Ch−¬ng 1:
Nguyªn lý lµm viÖc- kÕt cÊu c¬ b¶n
Bµi gi¶ng m¸y ®iÖn
Next
Néi dung
Back
1.1: CÊu t¹o cña m¸y ®iÖn mét chiÒu
1.2: Nguyªn lý lµm viÖc
1-3: c¸c l−îng ®Þnh møc
1.1: CÊu t¹o cña m¸y ®iÖn mét chiÒu
1. PhÇn tÜnh (Stato):
Next
Ch−¬ng I
Back
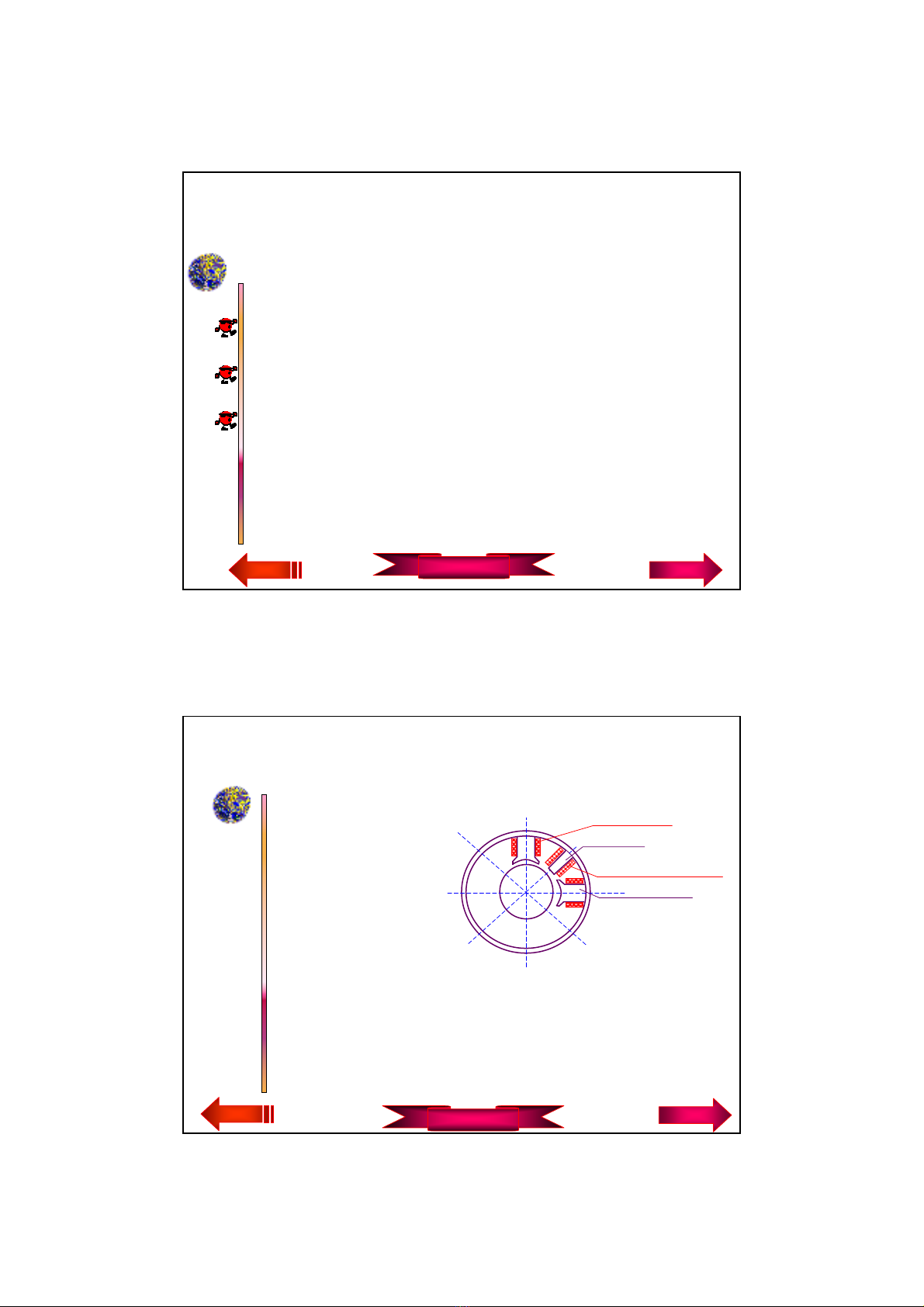
a) Cùc tõ chÝnh:
(Lµ bé phËn ®Ó
sinh ra tõ th«ng
kÝch thÝch)
b) Cùc tõ phô:
§Æt gi÷a c¸c cùc tõ chÝnh, dïng ®Ó c¶i thiÖn ®æi chiÒu.
c) G«ng tõ (vá m¸y):
d) C¸c bé phËn kh¸c:
N¾p m¸y: B¶o vÖ an toµn cho ng−êi vµ thiÕt bÞ.
C¬ cÊu chæi than: §−a dßng ®iÖn tõ phÇn quay ra m¹ch
ngoµi.
PhÇn I: m¸y ®iÖn mét chiÒu
Cùc tõ chÝnh
D©y quÊn cùc tõ phô
D©y quÊn cùc tõ chÝnh
Cùc tõ phô
Next
Ch−¬ng I
Back
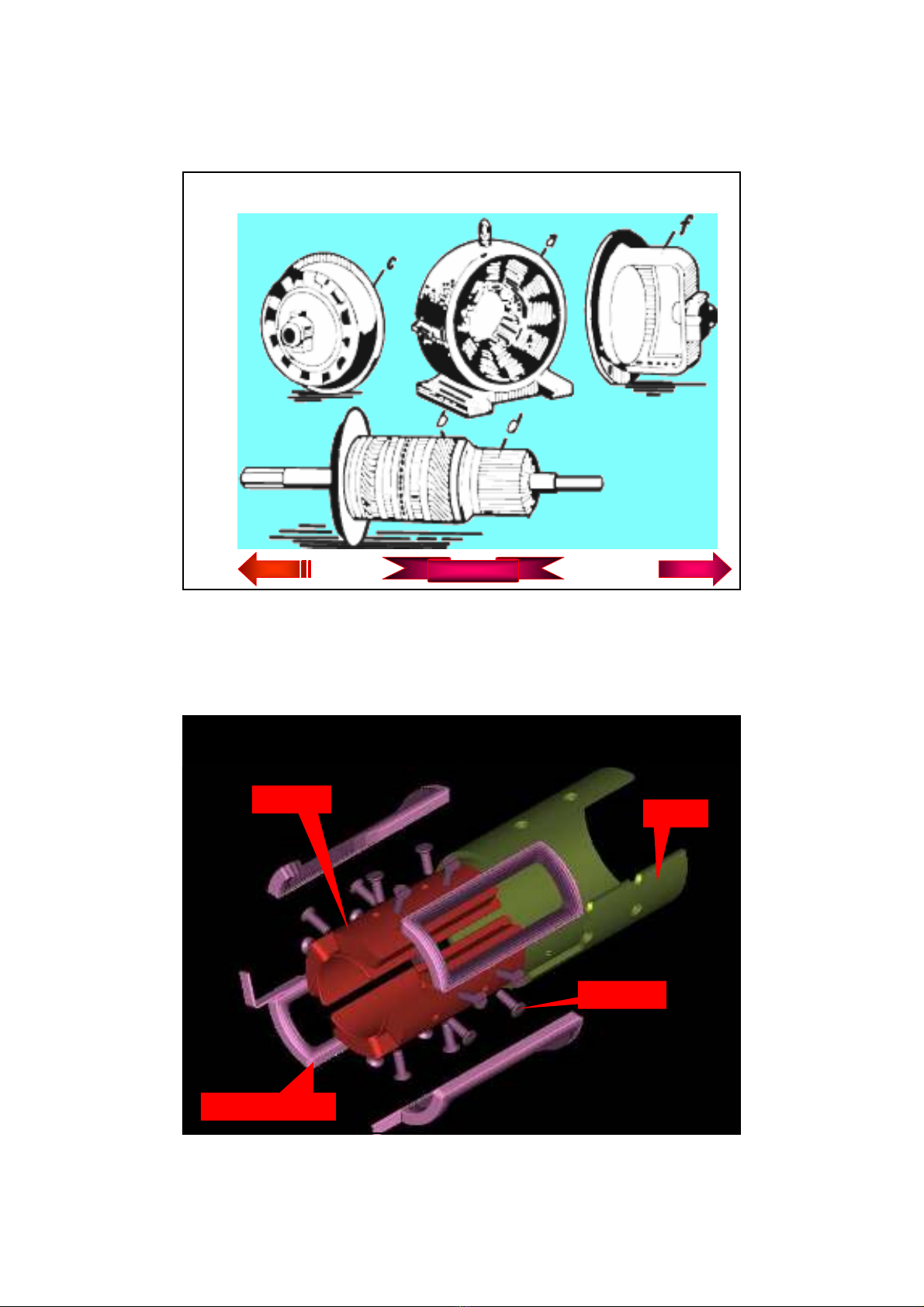
m¸y ®iÖn mét chiÒu
phÇn c¶m ®éng c¬ ®iÖn mét chiÒu
Cùc tõ vá
Bu l«ng
Cuén d©y












![Trắc nghiệm Mạch điện: Tổng hợp câu hỏi và bài tập [năm hiện tại]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251118/trungkiendt9/135x160/61371763448593.jpg)













