n đ nh c a các thanh th ngỔ ị ủ ẳ
Ch ng 2ươ
2.1.
2.1. n đ nh c a thanh th ng có liên k t c ng hai đ u ch u l c Ổ ị ủ ẳ ế ứ ở ầ ị ự
n đ nh c a thanh th ng có liên k t c ng hai đ u ch u l c Ổ ị ủ ẳ ế ứ ở ầ ị ự
nén đúng tâm ( lý thuy t Euler).ế
nén đúng tâm ( lý thuy t Euler).ế
2.2.
2.2.
n đ nh c a thanh th ng ch u l c đ t b t kỳ d c theo chi u Ổ ị ủ ẳ ị ự ặ ấ ọ ề
n đ nh c a thanh th ng ch u l c đ t b t kỳ d c theo chi u Ổ ị ủ ẳ ị ự ặ ấ ọ ề
d
dài thanh.
ài thanh.
2.3.
2.3.
n đ nh Ổ ị
n đ nh Ổ ị c aủ
c aủ thanh th ng ch u l c nén l ch tâm.ẳ ị ự ệ
thanh th ng ch u l c nén l ch tâm.ẳ ị ự ệ
2.4.
2.4.
nh h ng c a l c c t đ n các giá tr c a l c t i h n trongẢ ưở ủ ự ắ ế ị ủ ự ớ ạ
nh h ng c a l c c t đ n các giá tr c a l c t i h n trongẢ ưở ủ ự ắ ế ị ủ ự ớ ạ
các thanh th ng ch u nén u n.ẳ ị ố
các thanh th ng ch u nén u n.ẳ ị ố
2.5.
2.5.
n đ nh c a các thanh ghép.Ổ ị ủ
n đ nh c a các thanh ghép.Ổ ị ủ
2.6.
2.6.
Nh ng gi i h n c a lý thuy t Euler.ữ ớ ạ ủ ế
Nh ng gi i h n c a lý thuy t Euler.ữ ớ ạ ủ ế
2.7.
2.7.
S phá ho i c a c t có chi u dài c t b t kỳ : lý thuy t Rankin.ự ạ ủ ộ ề ộ ấ ế
S phá ho i c a c t có chi u dài c t b t kỳ : lý thuy t Rankin.ự ạ ủ ộ ề ộ ấ ế
2.8
2.8.
.
nh h ng c a hình d ng c a ti t di n ngang đ n s m t n Ả ưở ủ ạ ủ ế ệ ế ự ấ ổ
nh h ng c a hình d ng c a ti t di n ngang đ n s m t n Ả ưở ủ ạ ủ ế ệ ế ự ấ ổ
đ nh c a cị ủ
đ nh c a cị ủ t.ột.ộ
N i dungộ
N i dungộ
2.1.
2.1. n đ nh c a thanh th ng ch u l c nén đúng tâmỔ ị ủ ẳ ị ự
n đ nh c a thanh th ng ch u l c nén đúng tâmỔ ị ủ ẳ ị ự
( lý thuy t Euler)ế
( lý thuy t Euler)ế
Các thanh th ng ch u nén trong k t c u công trình có th là các ẳ ị ế ấ ể
c t, các d m gi ng ho c các thanh ch u nén c a dànộ ầ ằ ặ ị ủ
Khi l c nén đúng tâm tác d ng vào c t tăng d n đ n m t giá tr ự ụ ộ ầ ế ộ ị
t i h n ớ ạ c t s b u n theo m t ph ng nào đó tùy thu c vào ộ ẽ ị ố ộ ươ ộ
hình d ng hình h c c a c t và các khi m khuy t c a v t li u ạ ọ ủ ộ ế ế ủ ậ ệ
Lý thuy t Euler nghiên c u s m t n đ nh u n d c c a các thanh ế ứ ự ấ ổ ị ố ọ ủ
có đ m nh l n, tuy t đ i th ng, v t li u c u t o đ ng nh t và ộ ả ớ ệ ố ẳ ậ ệ ấ ạ ồ ấ
l c tác d ng m t cách chính xác d c theo đ ng tr c th ng qua ự ụ ộ ọ ườ ụ ẳ
tâm c a ti t di nủ ế ệ
V t li u làm vi c trong gi i h n đàn h iậ ệ ệ ớ ạ ồ
2.1.
2.1. n đ nh c a thanh th ng ch u l c nén đúng tâmỔ ị ủ ẳ ị ự
n đ nh c a thanh th ng ch u l c nén đúng tâmỔ ị ủ ẳ ị ự
( lý thuy t Eulerế
( lý thuy t Eulerế)
)
2.1.1. Thanh có hai đ u liên k t kh pầ ế ớ
y
G
x
b)
a)
z
v’
L
P
O
y
Ph ng trình vi phân c a đ ng đàn h i :ươ ủ ườ ồ
EJ
M
dz
vd
v
−==
2
2
"
Moment u n t i m t m t c t Z b t kỳố ạ ộ ặ ắ ấ
M(z) = Pth v
zBzAv
αα
cossin
+=
Ph ng trình đ ng đàn h i:ươ ườ ồ
EJ
P
th
=
2
α
A, B : h ng s , ằ ố
Đi u ki n biên : tề ệ i ạz = 0 và z = L, v = 0 B = 0 , A sinαL= 0, A ≠0 αL = k π
(2.1)
(2.2)
Hình 2.1.
2.1.
2.1. n đ nh c a thanh th ng ch u l c nén đúng tâmỔ ị ủ ẳ ị ự
n đ nh c a thanh th ng ch u l c nén đúng tâmỔ ị ủ ẳ ị ự
( lý thuy t Eulerế
( lý thuy t Eulerế)
)
2
2
l
EJ
P
th
π
=
Khi k = 1 l c t i ự ớ
h n Eulerạ
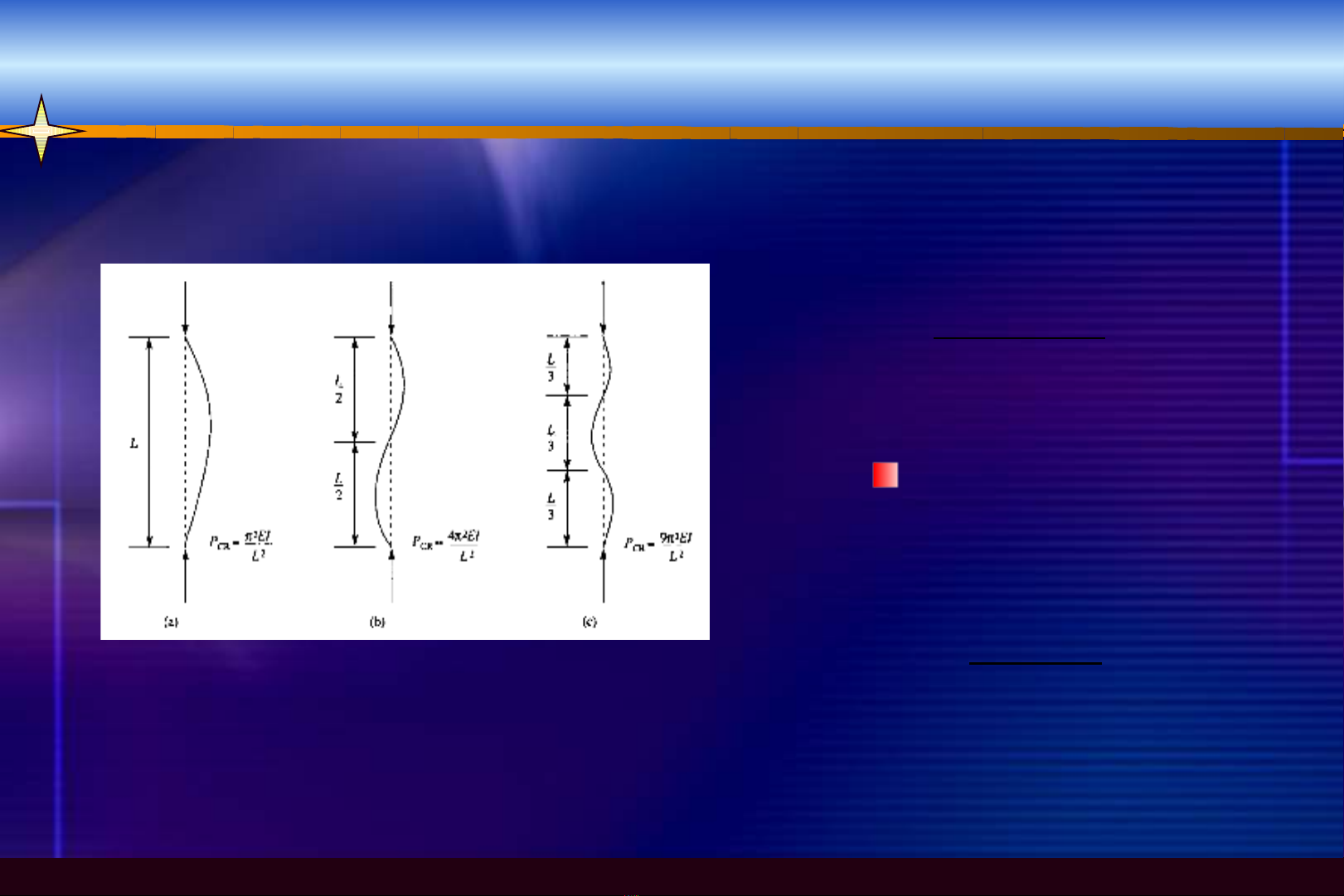
Hình 2.2. Các d ng m t n đ nh c a d m hai ạ ấ ổ ị ủ ầ
đ u kh p ng v i k = 1, 2, 3.ầ ớ ứ ớ
2
22
l
EJk
P
th
π
=
(2.3)
(2.4)