
02/01/2014
1
PHÂN TÍCH VÀ U T
CHNG KHOÁN
Ging viên: TS. Trn Phng Tho
Bmôn Thtrng Tài chính – Khoa Ngân hàng
THÁNG 1 / 2014
NI DUNG
1. Lãi sut
Lãi n
Lãi ghép nhiu ln trong nm
Lãi ghép liên tc
2. Giá tr ca dòng tin theo thi gian
Giá tr ca dòng tin n
Giá tr ca dòng tin u
Giá tr ca dòng tin u vô hn
Giá tr ca dòng tin tng trng
Lãi n: khi lãi c trtrên vn gc
Lãi ghép: khi lãi c trctrên vn gcvà trên phn lãi
sinh thêm tvn gc trong các khon thi gian trcó
Lãi ghép nhiu ln trong nm:
1. r = [1+(i/m)]m -1
Lãi ghép liên tc
11lim −=
+=
∞→
i
m
me
m
i
r
LÃI SUT
718.2
1
1lim ==
+
∞→
e
x
x
x
do
Các dng dòng tin
Dòng tiền đơn
Dòng tiền đều
Dòng tiền đều vô hạn
Dòng tiền có tăng trưởng
Nguyên tc tính PV và FV
Giả định toàn bộ tiền lãi thu được đều được tái đầu tư
với cùng mức lãi suất như vốn gốc
Các dòng tiền phát sinh vào cuối mỗi kỳ tính lãi
GIÁ TR CA DÒNG TIN THEO THI GIAN

02/01/2014
2
GIÁ TR TƠNG LAI CA DÒNG TIN ƠN
Lãi suất qua các năm không đổi: r
1
= r
2
= …= r
n
FV = CF
0
(1+r)
n
Lãi suất qua các năm không bằng nhau:
FV = CF
0
(1+r
1
) (1+r
2
) … (1+r
n
)
012 3 4 5 …
.
n
CFo
r1r2r3r4r5rn
Lãi suất không đổi : r
1
= r
2
= …= r
n
PV = CF
n
/(1+r)
n
Lãi suất thay đổi: r
1
, r
2, ….
r
n
PV = CF
n
/ (1+r
1
) (1+r
2
) … (1+r
n
)
GIÁ TR HIN TI CA DÒNG TIN ƠN
012 3 4 5 …
.
n
CFn
r1r2r3r4r5rn
GIÁ TR TƠNG LAI CA DÒNG TIN U
110
)1(....)1(r)C(1r)FV(n,
−
++++++=
n
rCrC
( ) ( )
(
)
−+
=+=
−
=
r
1r1
C1rn,FV
n
1
0
n
t
t
rC
t=0 t=1 t=2
C
C C
FV t=0 t=1 t=2
C
C C
GIÁ TR HIN TI CA DÒNG TIN U
( ) ( )
[
]
n
n
t
t
r
C
r
C
−
=
+=
+
=
r)(1-1
1
1
rn,PV
1
n
rCrC
−−
++++++= )1(....)1(r)C(1r)PV(n,
2-1

02/01/2014
3
Dòng
DòngDòng
Dòng tiền
tiềntiền
tiền đều
đềuđều
đều vô
vôvô
vô hạn
hạnhạn
hạn =
==
= dòng
dòngdòng
dòng tiền
tiềntiền
tiền đều
đềuđều
đều
kéo dài
mãi
mãimãi
mãi mãi
mãimãi
mãi
Giá trị hiện tại của dòng tiền đều vô hạn được tính như
đối với dòng tiền đều với n=
∞
Khi đó ta có:
PV = C/r
t=0 t=1 t=2
C
C C
DÒNG TIN U VÔ HN
Nm 0 1 2 3 … n …
Dòng tin C1 C2 C3 … Cn …
DÒNG TIN TNG TRNG
• Tng trng vi mt tc không i cho n vô hn
•Tng trng vi nhiu tc khác nhau
NG DNG
Các công thc vdòng tin cn ghi nhtrong tài chính
:
PV, FV, PMT, IRR, NPER, GOAL SEEK, …
CHNG 1
LI NHUN RI RO
VÀ DÒNG TiN
1B. LI NHUN VÀ RI RO
CA CHNG KHOÁN
NI DUNG
1. Li nhun và r i ro quá kh
2. Li nhun và r i ro k!v"ng
02/01/2014
4
Li nhun
Li nhun:
Thu nhp có c t# hot ng u t
Lãi : S tin c thanh toán t vic u t
Chênh l$ch giá: Do thanh i giá tr ca tài sn u t
Thco li nhun
Giá tr%tuy$ti
Li nhun = Lãi + chênh l$ch giá
Giá tr%tơng i
Li nhun = (lãi + chênh l$ch giá)/giá mua
Thc o li nhun
Trung bình sh"c
Là trung bình gi'nơn c a các kho'n li
nhun
n
RRR
R
n
....
21
+
+
=
Trung bình nhân
Là kho'n li nhun hàng nm nhnc khi
tái u tcác kho'n li nhun nhnc
trcó
1)1)....(1)(1(
21
−+++=
nn
RRRR
Ri Ro
Ri ro là s( không chc chn liên quan n
thu nhp t# u t
Phân loi ri ro:
- R i ro h$ thng: là r i ro tác ng n toàn b các
chng khoán trên th% tr)ng
- R i ro phi h$ thng: là r i ro ch* tác ng n mt
chng khoán ho+c mt nhóm các chng khoán c,
th-
Thc o ri ro
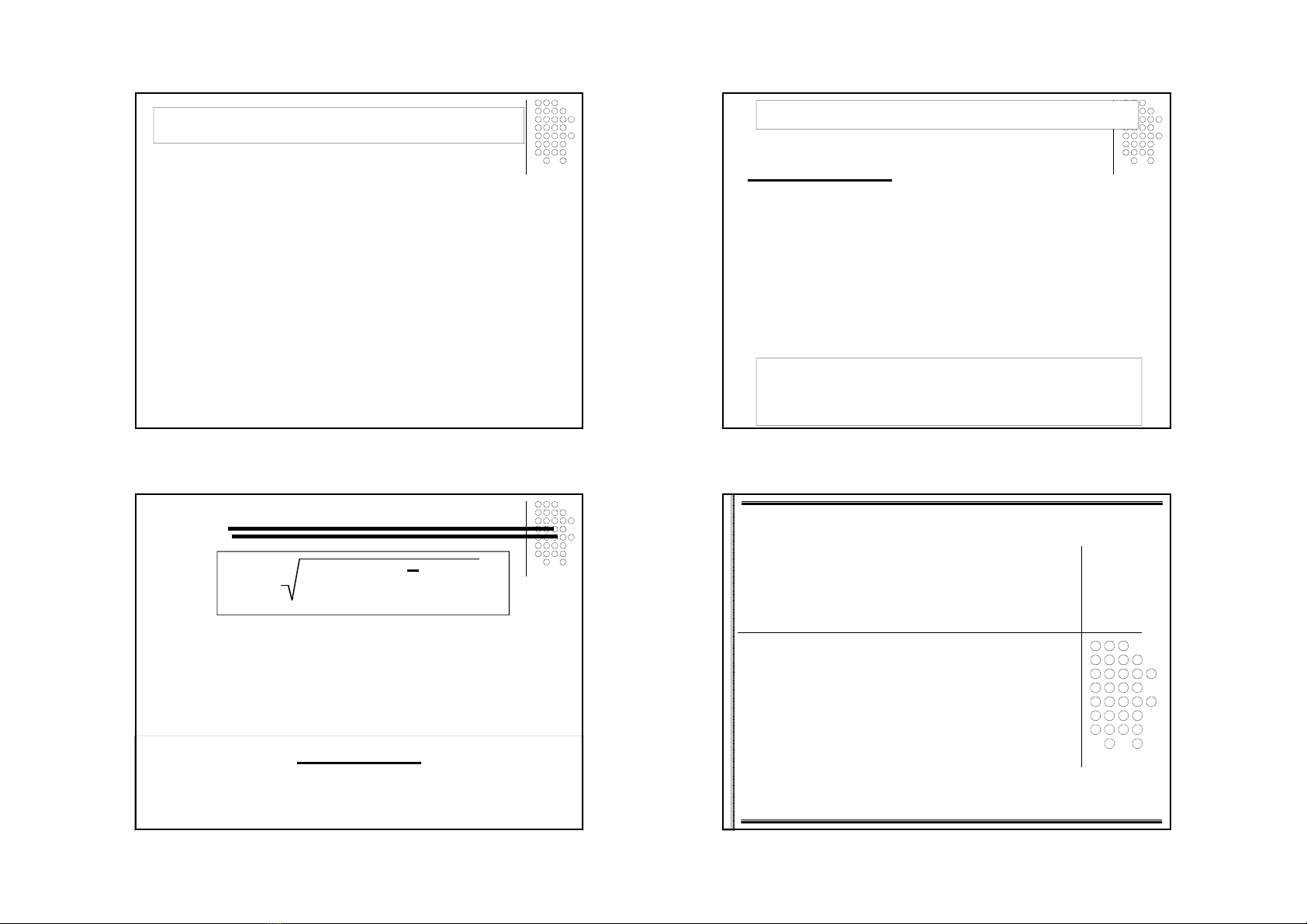
Thc o bình phơng r i ro c a mc sinh l)i
chính là phơng sai c tính theo công thc sau
("n" là s k! phát sinh li nhun):
l$ch chu.n c/ng có th- c s0 d,ng - o
l)ng r i ro
2
(R) SD
σ
=
n
RR
RVar
n
i
i
=
−
==
1
2
2
)(
)(
σ
Phơng sai m1u
Phơng sai tng th-
02/01/2014
5
H s phng sai
H$ s phơng sai (coefficient of variation) là t2 s
gi3a l$ch chu.n chia cho li nhun k! c a u
t. H$ s phơng sai o l)ng r i ro trên mt ơn
v% li nhun.
CV = σ/RA
H$ s phơng sai càng cao, r i ro trong hot ng
u t càng cao.
Li nhun kvng: c xác %nh d(a vào
-các kho'n li nhun (Ri) có th-phát sinh cho mt kho'n
u ttrong tơng lai và `li nhun này.
E(R) = Σ PiRi
Li nhun k vng
S S = Σ
ΣΣ
Σ( Ri- R )2( Pi)
l$chl$ch chu.nchu.n làlà ơnơn v%v% oo l)ngl)ng binbin thiênthiên
chungchung quanhquanh lili nhunnhun k!k!v"ngv"ng. .
l$chl$ch chu.nchu.n làlà cncn bcbc haihai c ac a binbin thiênthiên
ho+cho+c phơngphơng saisai...
S S = Σ
ΣΣ
Σ( Ri- R )2( Pi)
l$chl$ch chu.nchu.n làlà ơnơn v%v% oo l)ngl)ng binbin thiênthiên
chungchung quanhquanh lili nhunnhun k!k!v"ngv"ng. .
l$chl$ch chu.nchu.n làlà cncn bcbc haihai c ac a binbin thiênthiên
ho+cho+c phơngphơng saisai...
Ri ro k vng
NG DNG
Các công thc vdòng tin cn ghi nhtrong tài chính
:
AVERAGE, VAR, VARP, STDEV, STDEVP, CORREL,
COVAR, SLOPE, SUMPRODUCT
CHNG 1
1C. LI NHUN VÀ RI RO
CA DANH MC U T






















![Đề thi Tài chính cá nhân kết thúc học phần: Tổng hợp [Năm]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251015/dilysstran/135x160/64111760499392.jpg)


![Câu hỏi trắc nghiệm và bài tập Thị trường chứng khoán [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251001/kimphuong1001/135x160/75961759303872.jpg)
