
Gi i thu t tìm ki m trong đ thả ậ ế ồ ị
7.11.2004 Ch. 8: Elementary Graph Algorithms 2
Bi u di n các đ thể ễ ồ ị
ªHai cách bi u di n m t đ th ể ễ ộ ồ ị G = (V, E):
–Bi u di n ể ễ danh sách kề (adjacency list)
°m ng ảAdj g m ồV danh sách, 1 danh sách cho m i đnh trong ỗ ỉ V.
u V, Adj[u] ch a t t c các đnh ứ ấ ả ỉ v (ho c các con tr đn ặ ỏ ế
chúng) sao cho (u, v) E.
–Nh n xétậ
°Bi u di n danh sách k c n ể ễ ề ầ (V + E) memory. (Đ đn gi n, ể ơ ả
ký hi u ệV và E thay vì V và E.)

7.11.2004 Ch. 8: Elementary Graph Algorithms 3
Bi u di n các đ thể ễ ồ ị
(ti p)ế
–Bi u di n ể ễ ma tr n kậ ề (adjacency matrix)
°Đánh s đnh 1, 2,..., ố ỉ V
°A = (aij , ma tr nậ|V V
aij = 1 n u (ếi, j) E
0 trong các tr ng h p còn l i.ườ ợ ạ
–Nh n xétậ
°Bi u di n ma tr n k c n ể ễ ậ ề ầ (V 2) memory.
°Đ th th a (sparse), ồ ị ư E << V 2 : nên dùng danh sách kề .
°đ th đc (dense), ồ ị ặ E V 2 : nên dùng ma tr n kậ ề .
7.11.2004 Ch. 8: Elementary Graph Algorithms 4
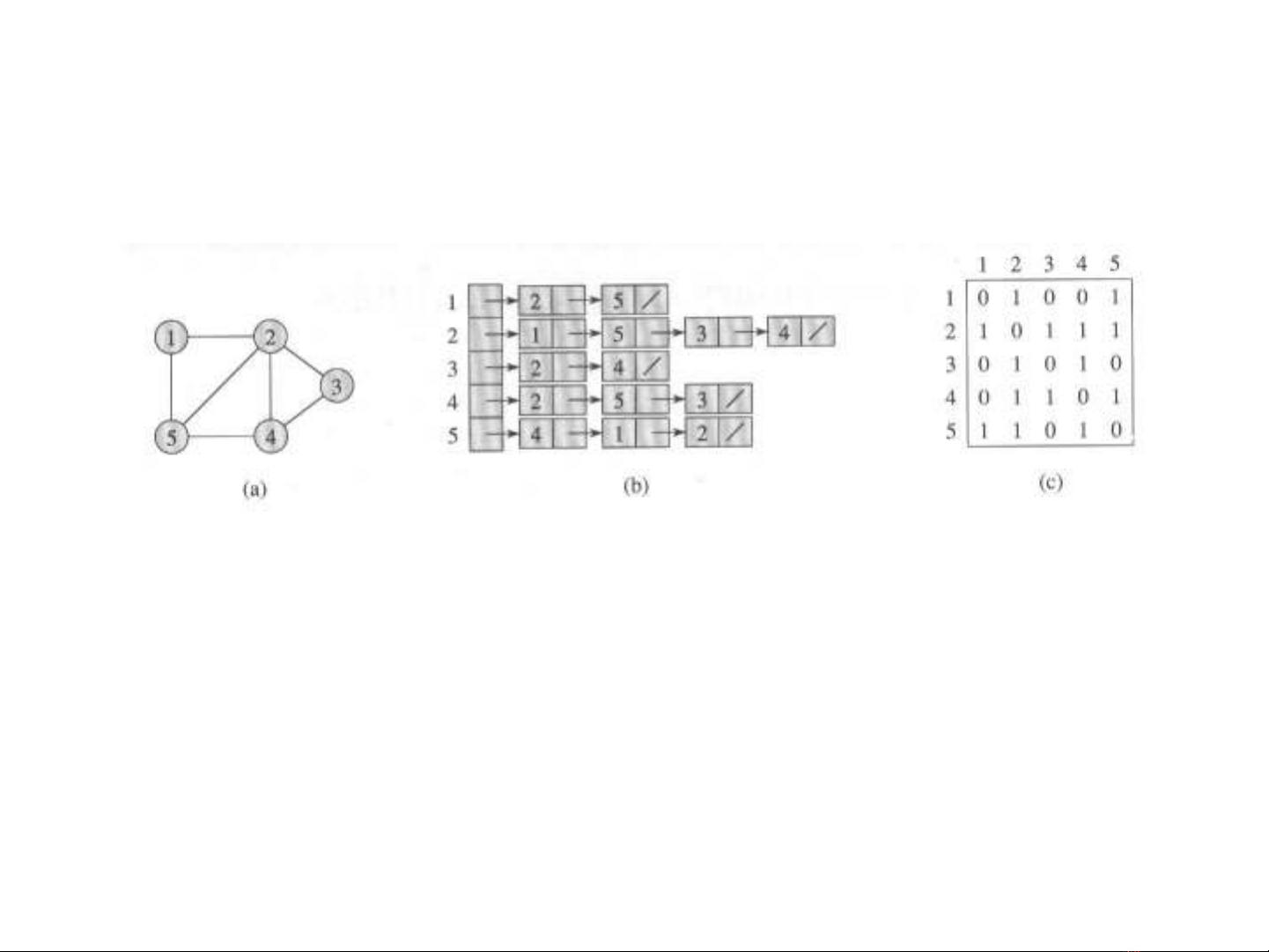
Bi u di n m t đ th vô h ngể ễ ộ ồ ị ướ
Bi u di nể ễ
b ng m t danh sách kằ ộ ề Bi u di nể ễ
b ng m t ma tr n kằ ộ ậ ề
M t đ th vô h ngộ ồ ị ướ
7.11.2004 Ch. 8: Elementary Graph Algorithms 5
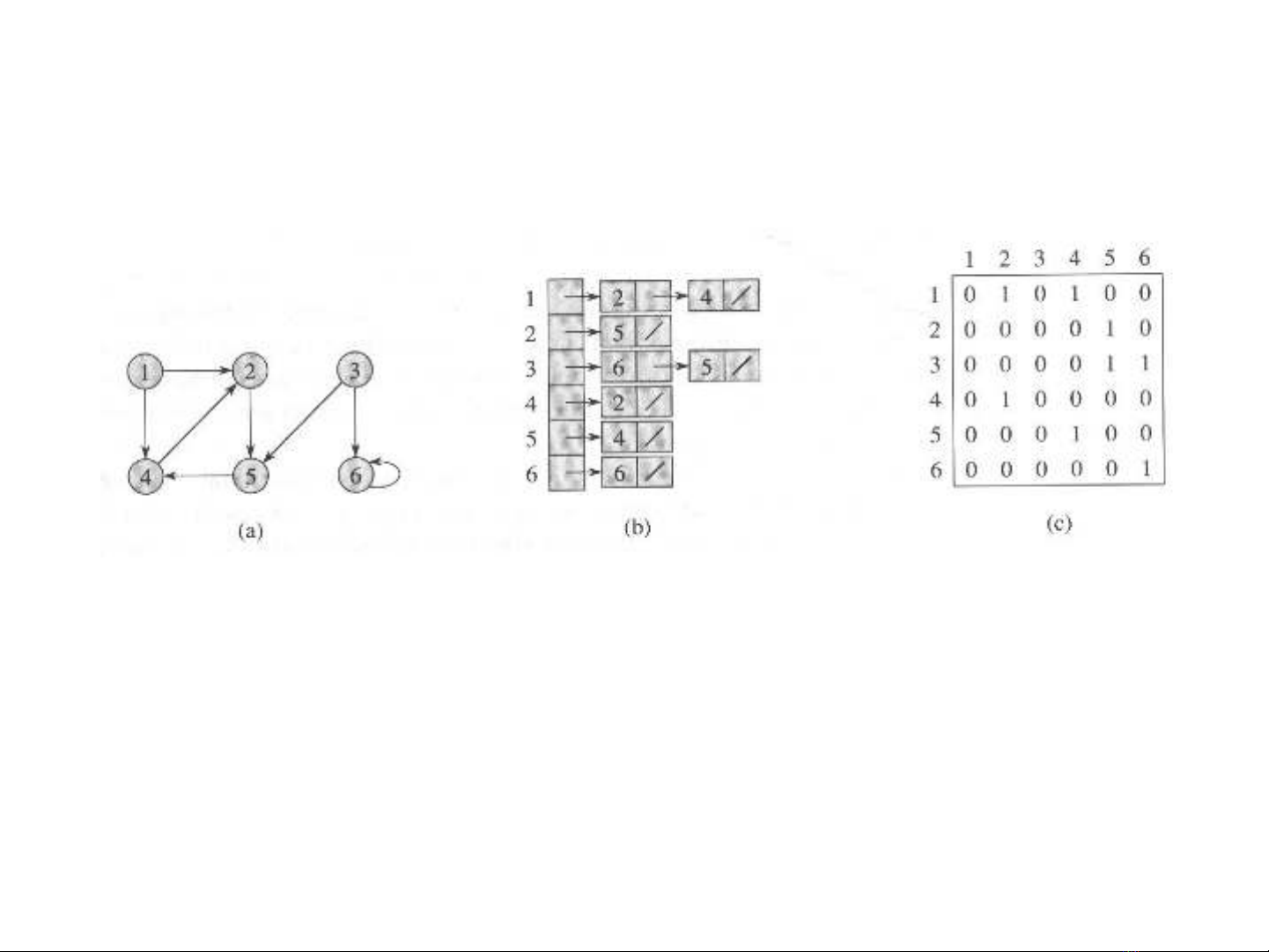
Bi u di n m t đ th có h ngể ễ ộ ồ ị ướ
Bi u di n b ngể ễ ằ
m t danh sách kộ ề Bi u di n b ng m tể ễ ằ ộ
ma tr n kậ ề
M t đ th có h ngộ ồ ị ướ


![Bài giảng Cấu trúc dữ liệu và giải thuật: Ôn tập [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2023/20230307/phuogchi205/135x160/121678182997.jpg)









![Đề thi kết thúc học phần Cấu trúc dữ liệu và thuật toán: Tổng hợp [Năm]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251229/bachtuoc999/135x160/77151767003271.jpg)













