
Hình này có ph i là hình bi u di n trả ể ễ bi u di n ể ễ
c a m t hình trong không gian hay không ?ủ ộ
Bài 5: PHÉP CHI U SONG SONGẾ
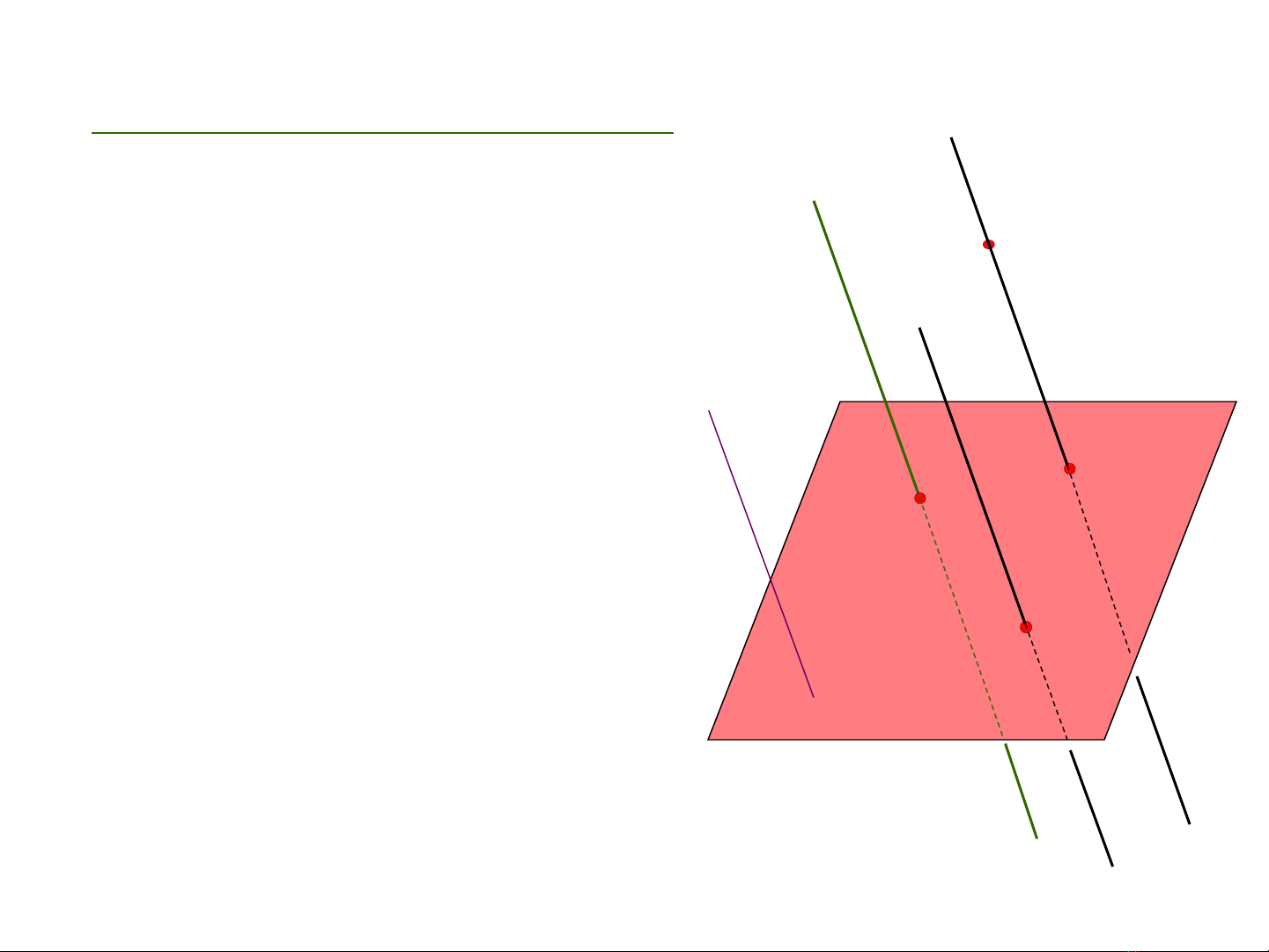
1. Đ nh nghĩa phép chi u song song:ị ế
Trong không gian cho (P) và đ ng ườ
th ng l c t (P).V i m i đi m M trong ẳ ắ ớ ỗ ể
không gian, v đ ng th ng đi qua M ẽ ườ ẳ
và song song ho c trùng v i l. Đ ng ặ ớ ườ
th ng này c t (P) tai Mẳ ắ ’ nào đó.
Phép đ t t ng ng m i đi m M ặ ươ ứ ỗ ể
trong không gian v i đi m Mớ ể ’ c a m t ủ ặ
ph ng (P) nh trên g i làẳ ư ọ phép chi u ế
song song lên m t ph ng (P) theo ặ ẳ
ph ng ươ l .
P)
l
M
M'
B
a
M
+ (P): g i là m t ph ng chi u.ọ ặ ẳ ế
+ l g i là ph ng chi u.ọ ươ ế
+ M’ g i là hình chi u song song (ho c nh) c a M.ọ ế ặ ả ủ
P)
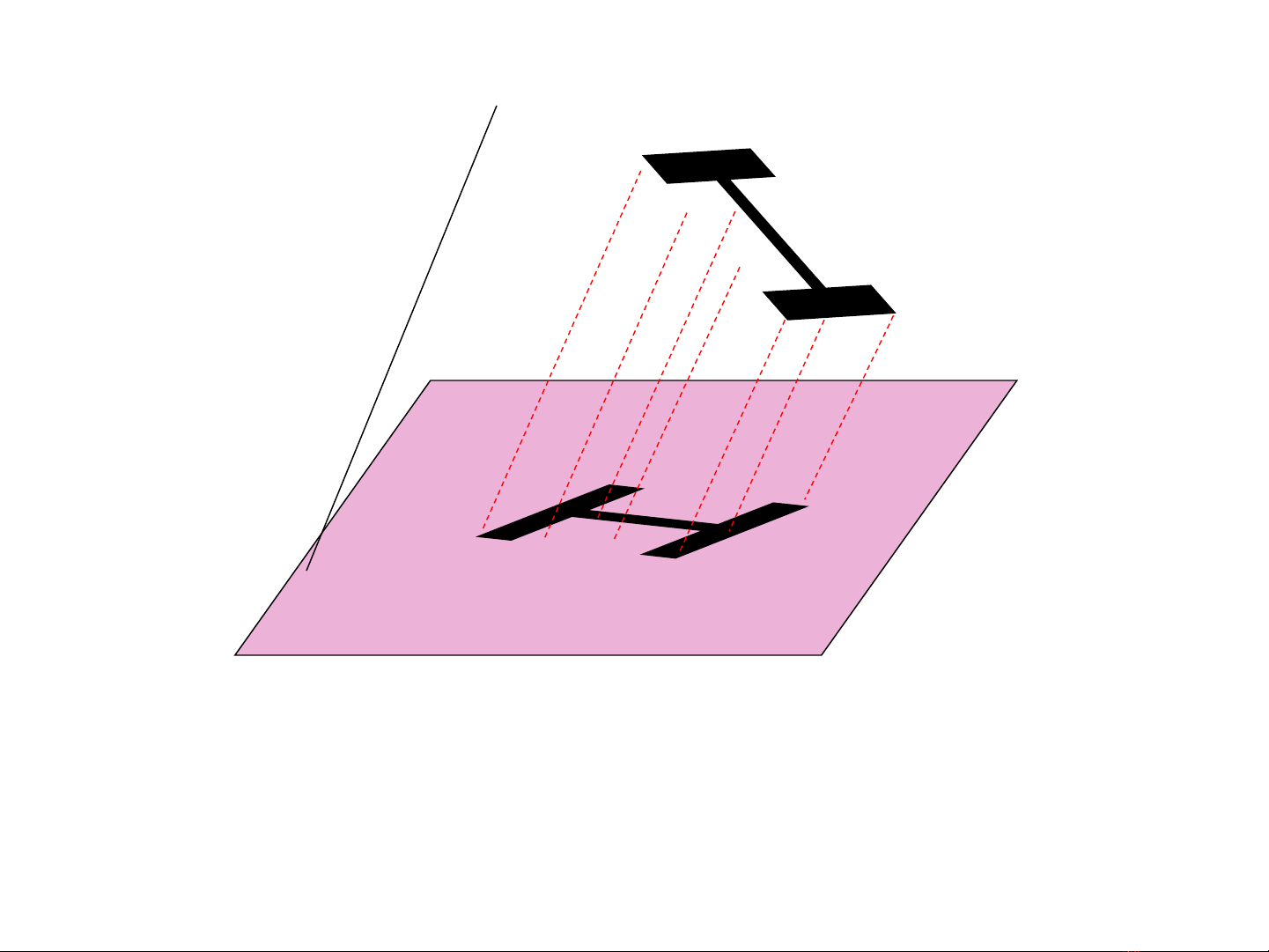
Cho hình H. T p h p ậ ợ H’ g m hình chi u song song c a t t ồ ế ủ ấ
c các đi m thu c ả ể ộ H g i là hình chi u song song (ho c nh) ọ ế ặ ả
c a hình ủH qua phép chi u nói trên.ế

2. Tính ch t:ấ
Ta ch xét hình chi u song song c a ỉ ế ủ
các đ an th ng ho c đ ng th ng ọ ẳ ặ ườ ẳ
không song song và không trùng v i ớ
ph ng chi u.ươ ế
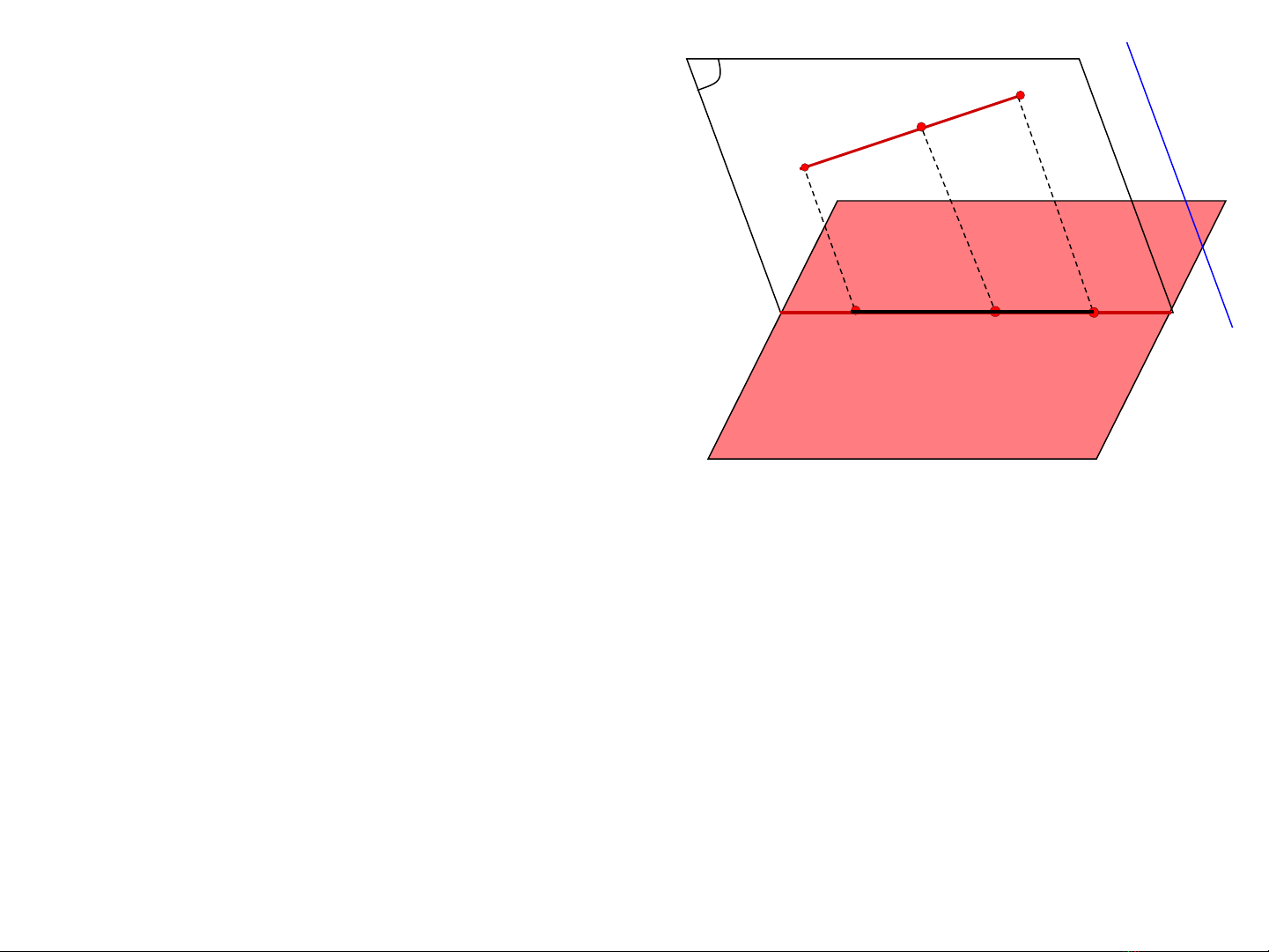
Tính ch t 1:ấ
Hình chi u song song c a ế ủ
m t đ ng th ng là m t ộ ườ ẳ ộ
đ ng th ng.ườ ẳ
P)
Q
M
M'
a
l
a’
H QU :Ệ Ả
Hình chi u song song c a m t đ an th ng là m t ế ủ ộ ọ ẳ ộ
đ an th ng, c a m t tia là m t tia.ọ ẳ ủ ộ ộ
M
N
M’N’


























