
Chƣơng 3
Phƣơng trình và hệ phƣơng trình vi phân
Mở đầu. Các bài toán thường gặp có thể 2 loại:
* Bài toán Côsi : là bài toán dạng phương trình vi phân với
điều kiện bổ sung (điều kiện ban đầu) đã cho tại không quá
một điểm.
C -hằng số tích phân, phụ thuộc điều kiện ban đầu
-Mỗi giá trị của C 1 nghiệm xác định.
-Xác định C cần biết thêm 1 điều kiện ban đầu, ví dụ
Ví dụ: Cho phương trình vi phân cấp 1: y’ = 2x + 1; (a)
-Nghiệm tổng quát : y = x2+ x + C; (b)
y(x=1) = 2; (c) (b) C = 0;
Nghiệm của (a) là y = x2+ x thoả mãn (a) và (c).
Bài toán tìm hàm số y(x) thoả mãn p/t vi phân (a) và điều kiện
ban đầu (c) bài toán Côsi.
CuuDuongThanCong.com https://fb.com/tailieudientucntt

Chƣơng 3
Phƣơng trình và hệ phƣơng trình vi phân
Bài toán Côsi đối với phương trình vi phân cấp 1:
-Cho khoảng [x0, X]
-Tìm hàm số y = y(x) xác định trên [x0, X] thoả mãn:
y’ = f(x,y);
Xxx0
y(x0) = η;
( 1 )
( 2 )
Trong đó f(x, y) – hàm đã biết; η- sốthực cho trước
( 2 ) - điều kiện Côsi hay điều kiện ban đầu.
CuuDuongThanCong.com https://fb.com/tailieudientucntt

Chƣơng 3
Phƣơng trình và hệ phƣơng trình vi phân
* Bài toán biên.
Bài toán giải phương trình vi phân với điều kiện bổ sung được
cho tại nhiều hơn 1 điểm.
-Cho khoảng [a, b];
-Tìm hàm y = y(x) trên [a, b] thoả mãn:
Trong nhiều trường hợp giải gần đúng .
y’ + p(x)y’ +q(x,y) = f(x);
bxa
( 3 )
với điều kiện y(a) = α; y(b) = β( 4 )
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Chƣơng 3
Phƣơng trình và hệ phƣơng trình vi phân
Giải bài toán Côsi.
Phương pháp chuỗi Taylo. y’ = f(x, y);
Xxx0
y(x0) = η;
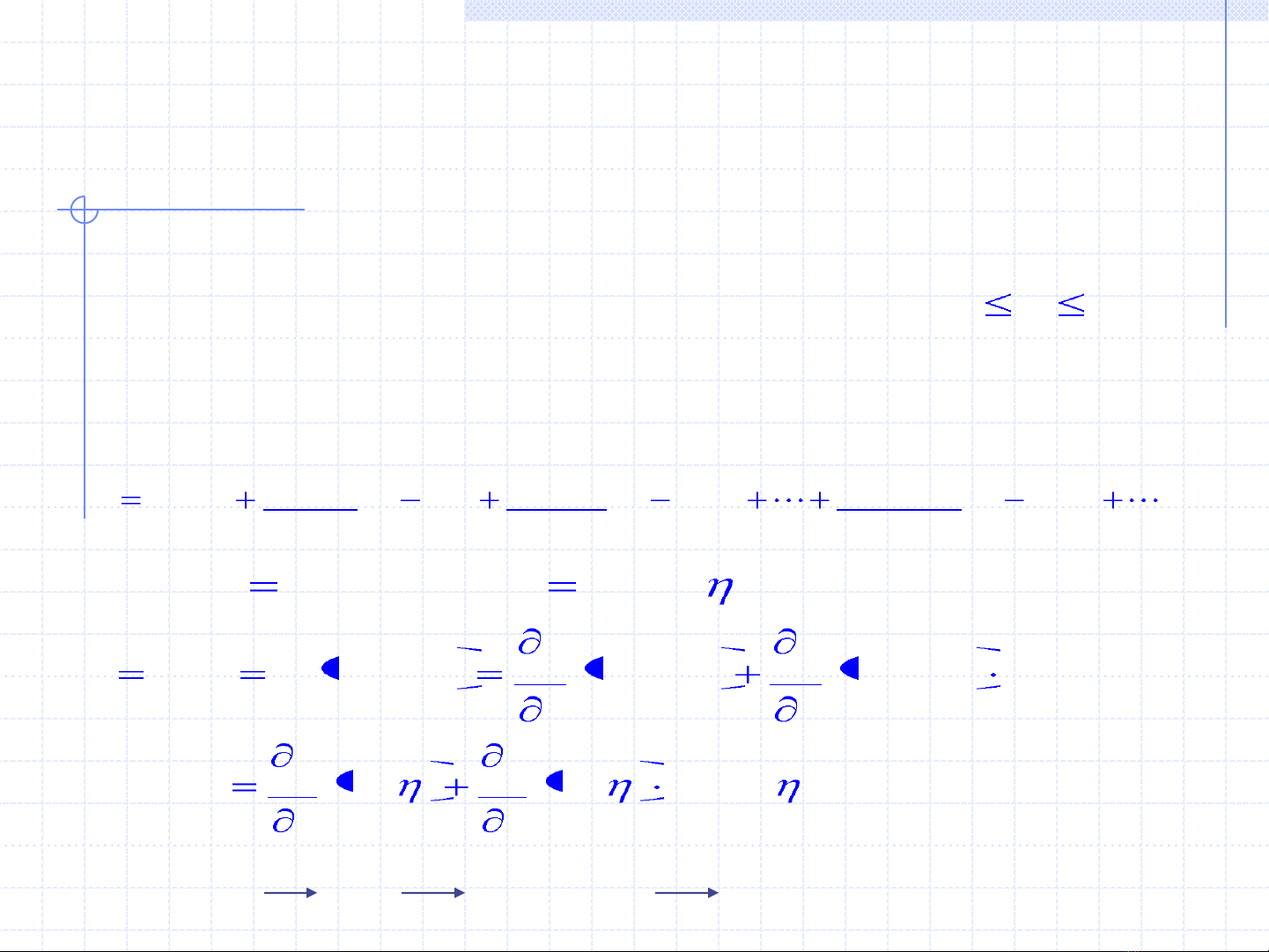
Khai triển nghiệm y(x) tại x = x0:
k
k
xx
k
xy
xx
xy
xx
xy
xyxy )(
!
)(
)(
!2
)("
)(
!1
)('
)()( 0
0
)(
2
0
0
0
0
0
( 5 )
);,())(,()(' 0000 xfxyxfxy
( 6 )
);(')(,)(,')(,)''(" xyxyx
y
f
xyx
x
f
xyxfyy
Tương tự y’” y(3)(x0)chuỗi ( 5 ).
);,(,,)(" 0000 xfx
y
f
x
x
f
xy
( 7 )
CuuDuongThanCong.com https://fb.com/tailieudientucntt



























