PHƢƠNG PHÁP SỐ
TRONG CÔNG NGHỆ HÓA HỌC
Mã học phần: CH3454
TS. Nguyễn Đặng Bình Thành
BM:Máy & TBCN Hóa chất
Numerical Methods in Chemical Engineering
Tuần 6
CuuDuongThanCong.com https://fb.com/tailieudientucntt
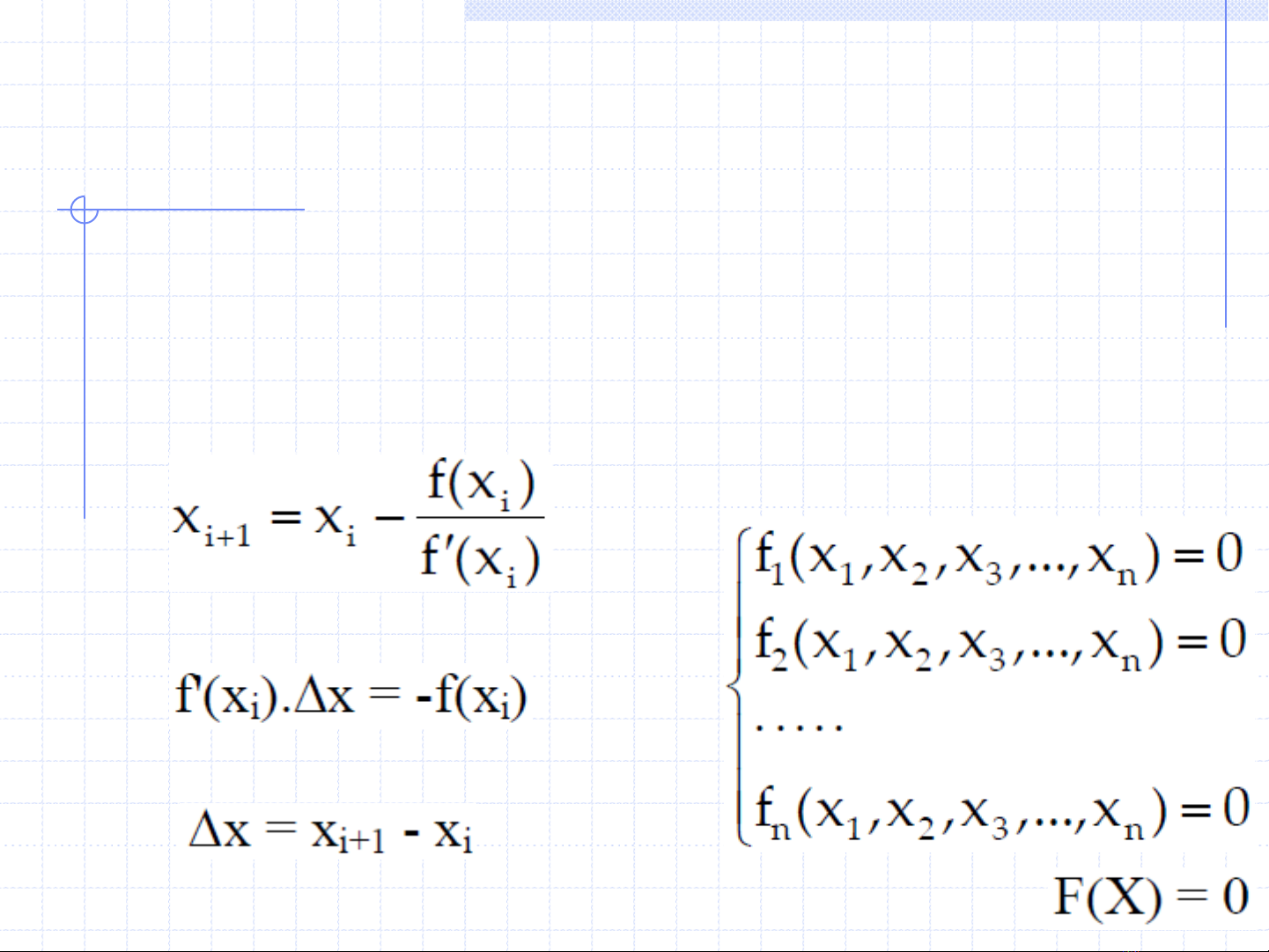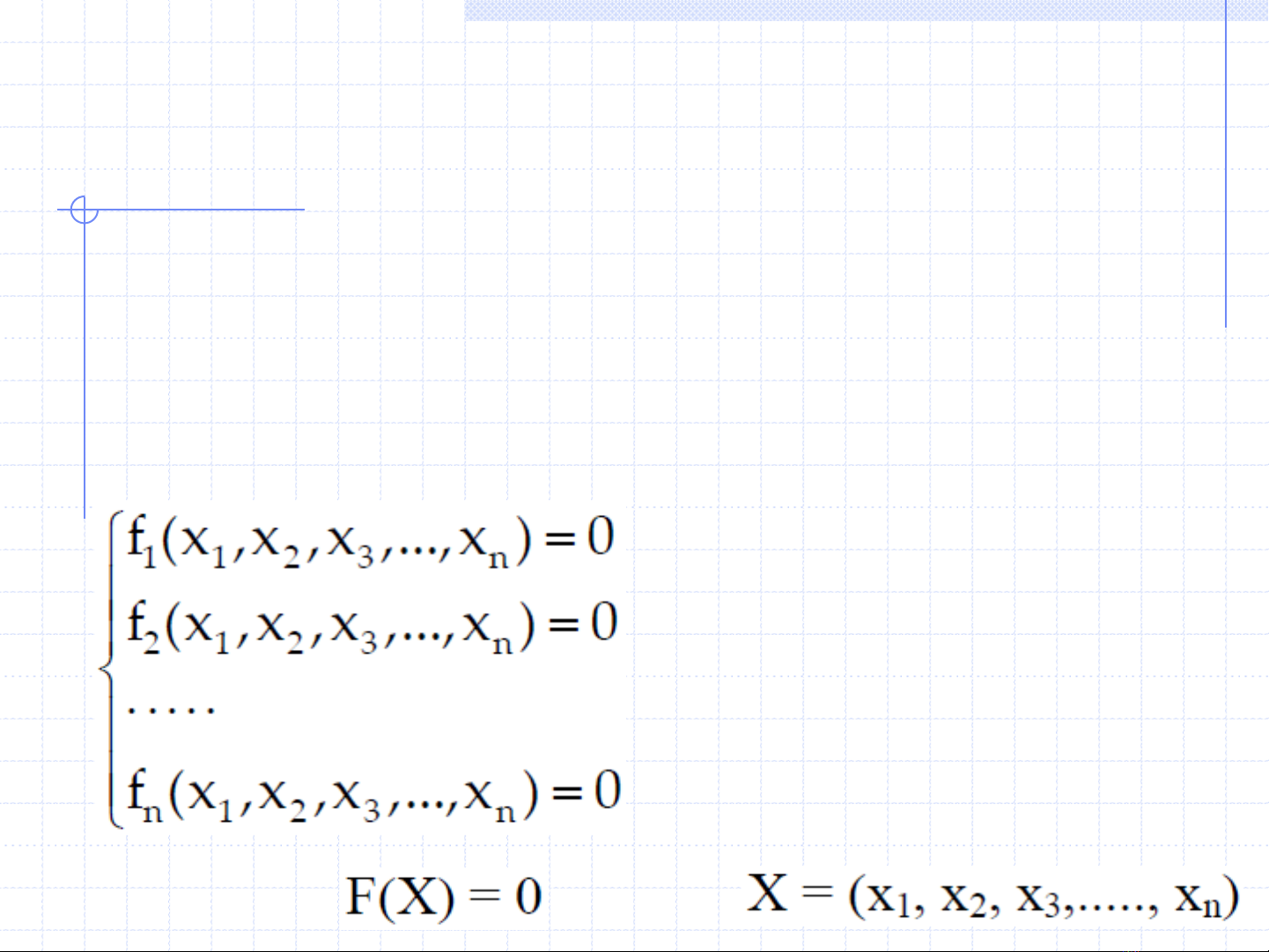
Chƣơng 1. Các phƣơng pháp giải phƣơng
trình và hệ phƣơng trình
1.2 Phƣơng pháp giải phƣơng trình và hệ phƣơng trình
phi tuyến
Giải hệ phương trình phi tuyến bằng phương pháp Newton
Phƣơng pháp Newton có thể tổng quát hóa để giải hệ phƣơng trình phi
tuyến có dạng:
Dạng ma trận: Trong đó:
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Chƣơng 1. Các phƣơng pháp giải phƣơng
trình và hệ phƣơng trình
1.2 Phƣơng pháp giải phƣơng trình và hệ phƣơng trình
phi tuyến
Giải hệ phương trình phi tuyến bằng phương pháp Newton
Công thức Newton với phƣơng trình 1 biến:
Hay:
Với:
CuuDuongThanCong.com https://fb.com/tailieudientucntt
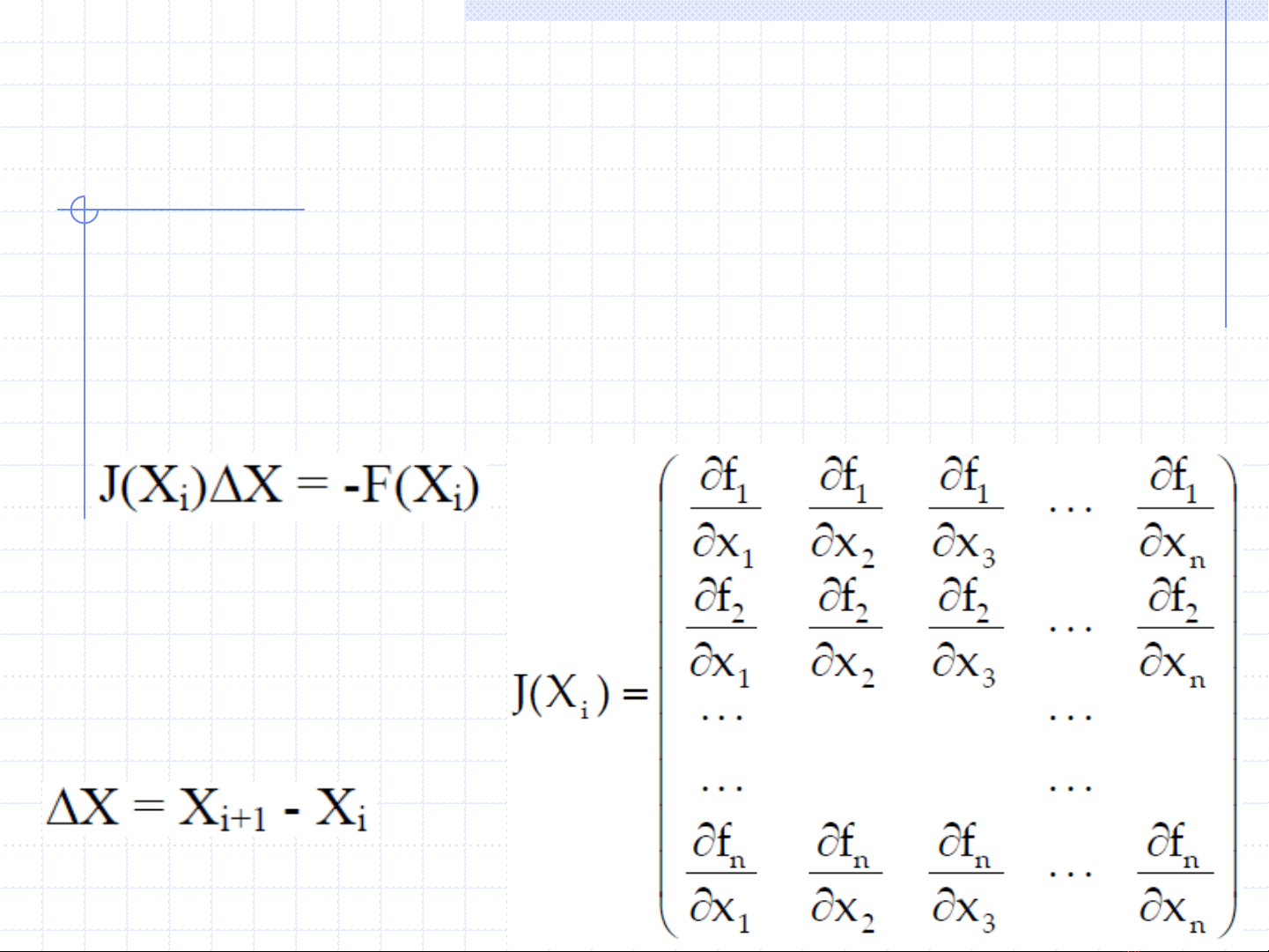
Chƣơng 1. Các phƣơng pháp giải phƣơng
trình và hệ phƣơng trình
1.2 Phƣơng pháp giải phƣơng trình và hệ phƣơng trình
phi tuyến
Giải hệ phương trình phi tuyến bằng phương pháp Newton
Đối với hệ phƣơng trình phi tuyến, công thức Newton tổng quát:
Trong đó J(Xi) là ma trận
(toán tử) Jacobi. Nó là ma
trận cấp n có dạng:
Và:
CuuDuongThanCong.com https://fb.com/tailieudientucntt
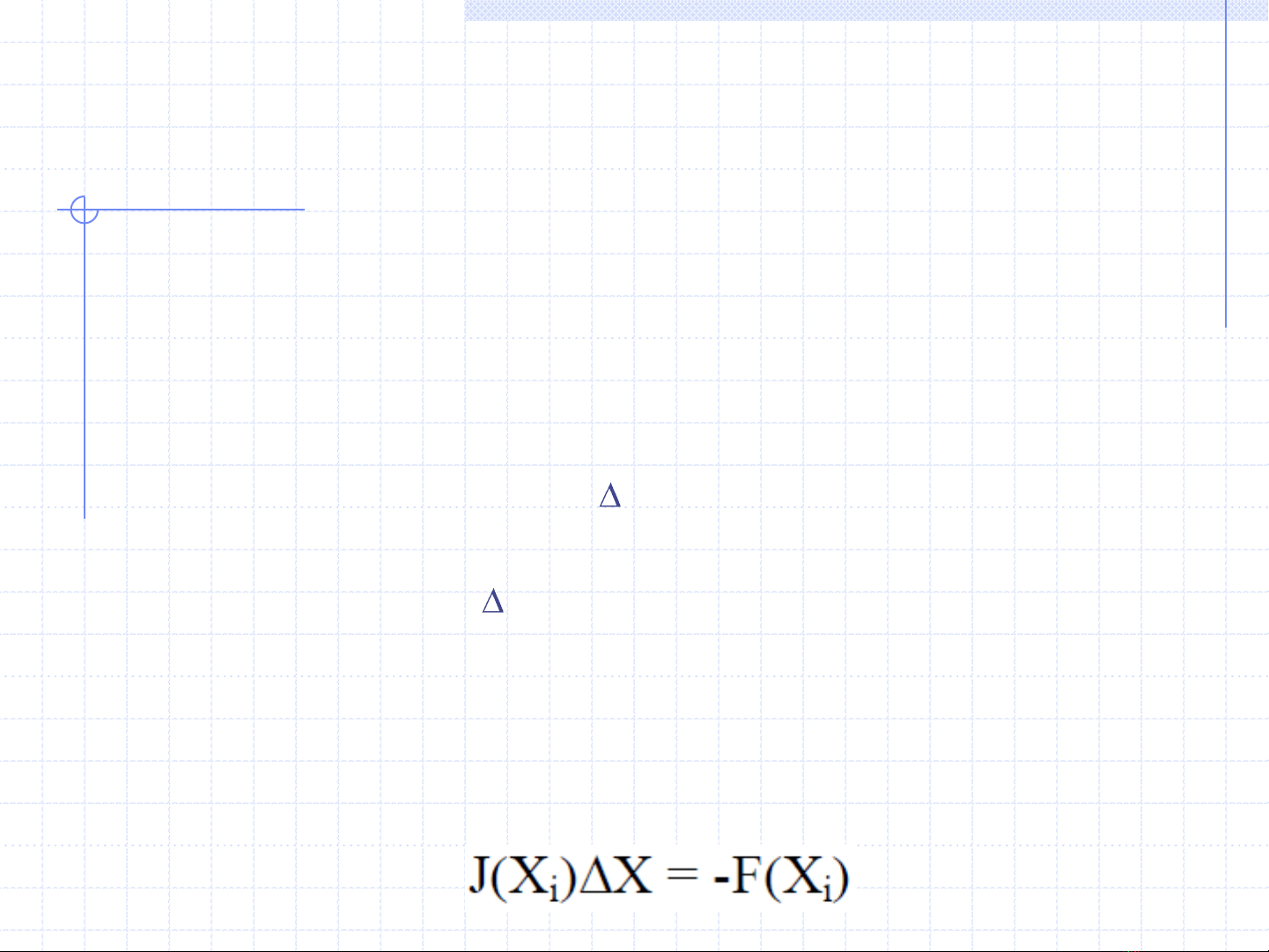
Chƣơng 1. Các phƣơng pháp giải phƣơng
trình và hệ phƣơng trình
1.2 Phƣơng pháp giải phƣơng trình và hệ phƣơng trình
phi tuyến
Giải hệ phương trình phi tuyến bằng phương pháp Newton
Phƣơng pháp Newton giải hệ phƣơng trình phi tuyến là phƣơng pháp
tuyến tính hóa hệ phƣơng trình đã cho thành một hệ phƣơng trình
tuyến tính mà biến số của hệ là X.
Nhƣ vậy ở mỗi bƣớc lặp (bƣớc thứ i), cần phải giải một hệ phƣơng trình
tuyến tính với biến số là Xicho đến khi đƣợc nghiệm gần đúng.
Vì vậy: việc giải hệ phương trình phi tuyến bằng
phương pháp Newton là lặp lại việc giải hệ phương
trình tuyến tính:
CuuDuongThanCong.com https://fb.com/tailieudientucntt