THIẾT KẾHỆTHỐNG ĐIỀU KHIỂN
ThS. Nguyễn Hữu Quang
Bộmôn GCVL & DCCN
Nội dung môn học (dựkiến)
•Giới thiệu
• Mô hình toán học của các hệthống kỹthuật
• Phân tích và thiết kếcác hệthống điều khiển
•Ứng dụng phần mềm MATLAB
•Phần tùy chọn (thay thếcho bài thi giữa kỳ): Project “Điều khiển tốc độ
động cơ một chiều, sửdụng vi điều khiển”
2
Tài liệu tham khảo chính
•Lý thuyết điều khiển tuyến tính – Nguyễn Doãn Phước
•Matlab & Simulink dành cho kỹ sư điều khiển tự động – Nguyễn Phùng
Quang
•Modern control engineering –4
th – Katsuhiko Ogata (pdf file)
3
PHẦN MỘT: MÔ HÌNH TOÁN HỌC
• Mô hình phương trình vi phân
• Mô hình hàm truyền đạt
• Mô hình trạng thái
•Tuyến tính hóa mô hình
4
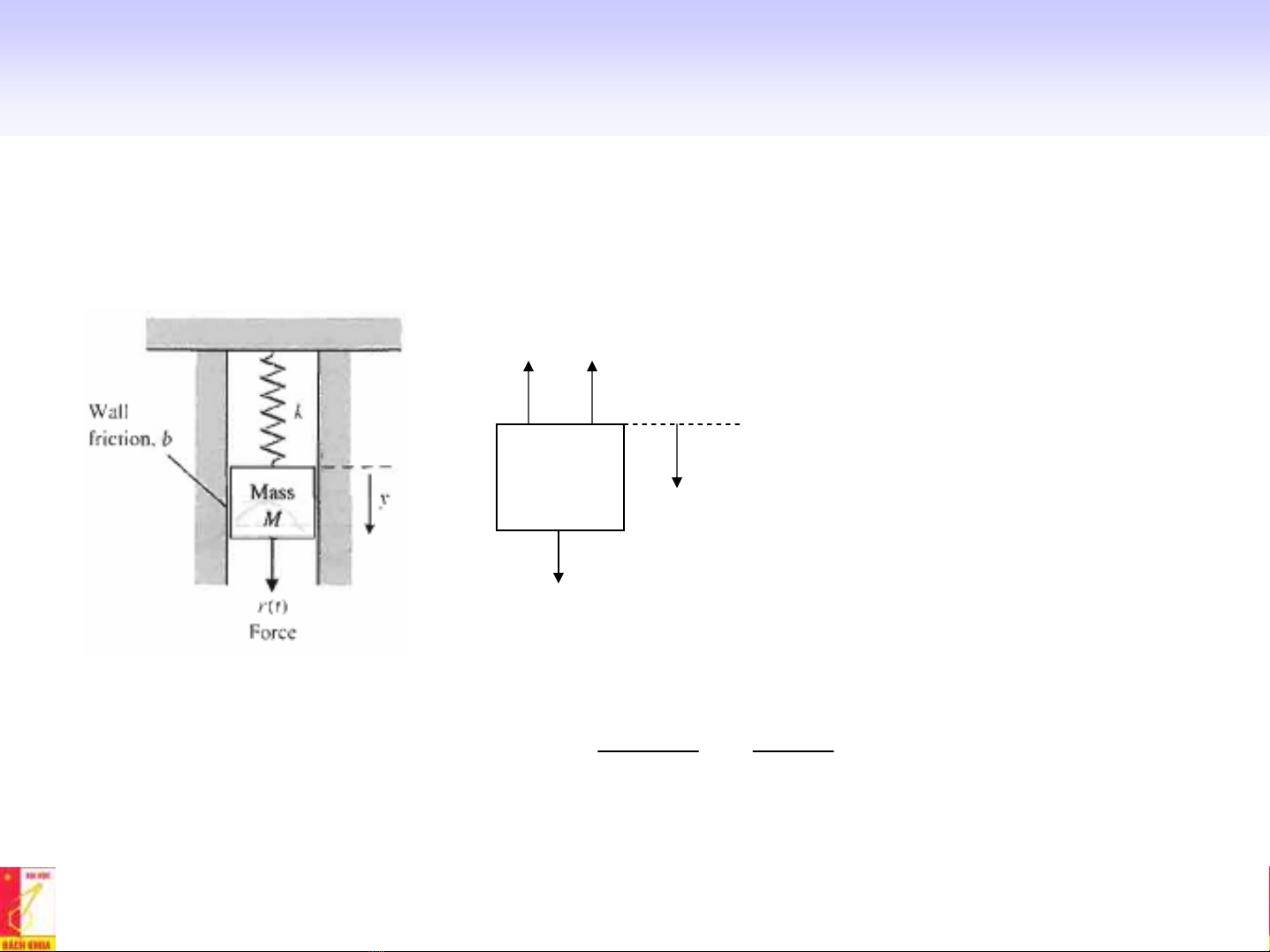
Phương trình vi phân
•Mô tảhệthống kỹthuật bằng phương trình vi phân
Ví dụ1: Hệvật – lò xo
M
ky
r(t)
y
by
(
)() () ()
2
2
dyt dyt
M
bkytrt
dt dt
++=
Áp dụng định luật Newton:
5