Ng i tri nh ba y: ươ
TS. Hoa ng Manh Thăng
Bia Karnaugh (K-map)
K-map cung câp ca ch th c hi n ự ệ tôi thiêu
ho a dang tông ca c ti ch hay ti ch ca c tông
d i dang đô hoa ươ
Ca c minterm co thê đc kêt h p v i ươ ơ ơ
nhau khi chu ng kha c nhau duy nhât môt
biên
f(x,y,z)=xyz+xyz’=xy(z+z’)=xy(1)=xy
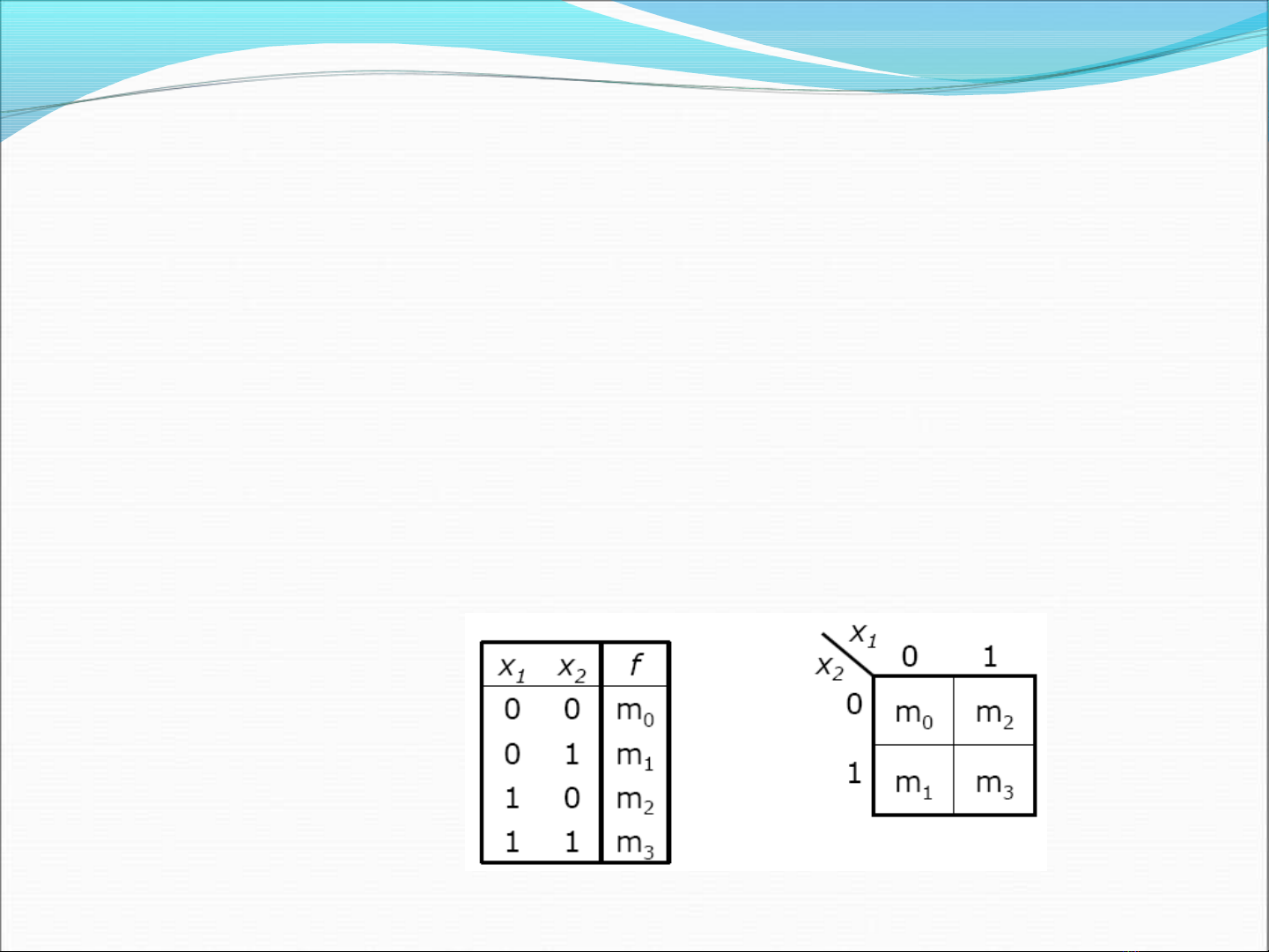
K-map mô ta vi c ệkêt h p na y băng hi nh ơ
Chương 3 3
Khoa ĐT-VT, Đại học Bách Khoa Hà nội
Tiến sỹ Hoàng Mạnh Thắng
Bia Karnaugh (cont.)
K-map thay thê cho bang chân ly khi biêu diên môt
biêu th c ư
K-map ch a ca c cell t ng ng v i ha ng cua ư ươ ư ơ
bang chân ly
Môi cell t ng ng v i môt minterm ươ ư ơ
Vi du:
Chương 3 4
Khoa ĐT-VT, Đại học Bách Khoa Hà nội
Tiến sỹ Hoàng Mạnh Thắng
Bia Karnaugh (cont.)
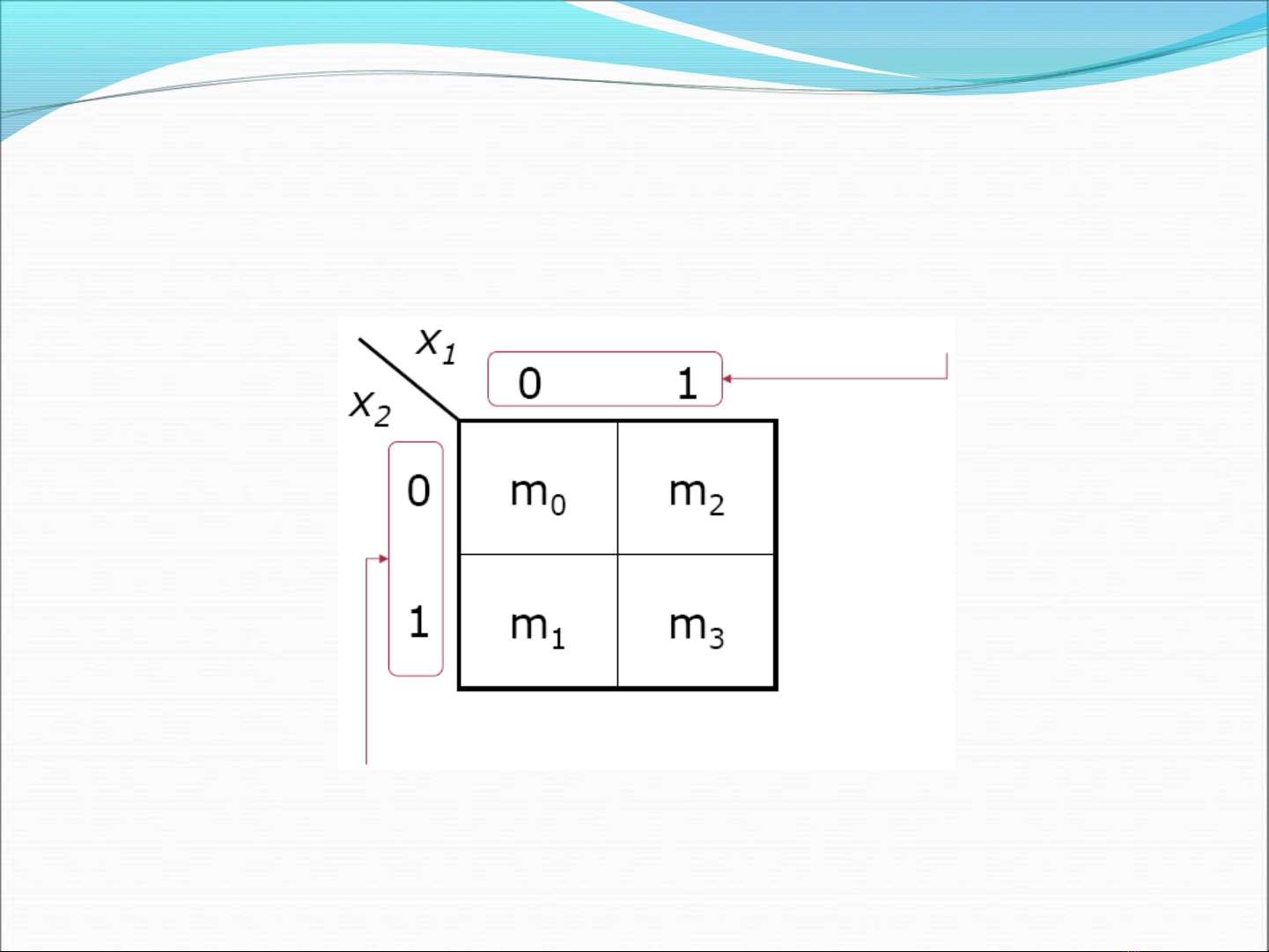
Ca)c gia) tri* cho biê)n thư) nhâ)t
Ca)c gia) tri* cho biê)n thư) 2
Chương 3 5
Khoa ĐT-VT, Đại học Bách Khoa Hà nội
Tiến sỹ Hoàng Mạnh Thắng