


Ng i tri nh ba y: ươ
Ti n sế ỹ Hoa ng Manh Thăng

Mach logic
Mach logic th c hiên ca c ư
hoat đông trên ca c ti n hiêu
sô:
Đc th c hiên d i dang ươ ư ươ
mach điên t v i gia tri la ca c ư ơ
ti n hiêu gi i han vê ca c biên ơ
co gia tri r i rac ơ
Mach logic nhi phân chi co 2
gia tri, 0 va 1
Dang tông qua t cua mach
logic la mang chuyên mach
X1
X2
X3
Y1
Y2
Y3
XmYm
Mang chuyên mach
Cac gia tri rơi rac
3
Khoa ĐT-VT, Đại học Bách Khoa Hà nội
Tiến sỹ Hoàng Mạnh Thắng

Đai sô Boolean
ng dung tr c tiêp va o mang chuyên mach: Ư ư
La m viêc v i thiêt bi 2 trang tha i ơ đai sô Boolean 2
gia tri
Du ng ca c biên Boolean (X,Y...) đê biêu diên đâ u va o
va đâ u ra cua mang chuyên mach
Biên chi co thê nhân môt trong 2 gia tri, 0 hoăc 1
Ca c biên na y ko phai la ca c sô nhi phân, đn gian no ơ
chi la biêu diên 2 trang tha i cua biên Boolean,
Nhi n chung, no không la điên a p , măc du , trong môt sô
mach điên, no đc du ng đê biêu diên m c điên a p ươ ư
cao/thâp đâ u va o hoăc đâ u ra, ơ
4
Khoa ĐT-VT, Đại học Bách Khoa Hà nội
Tiến sỹ Hoàng Mạnh Thắng
Cac biên va cac ham
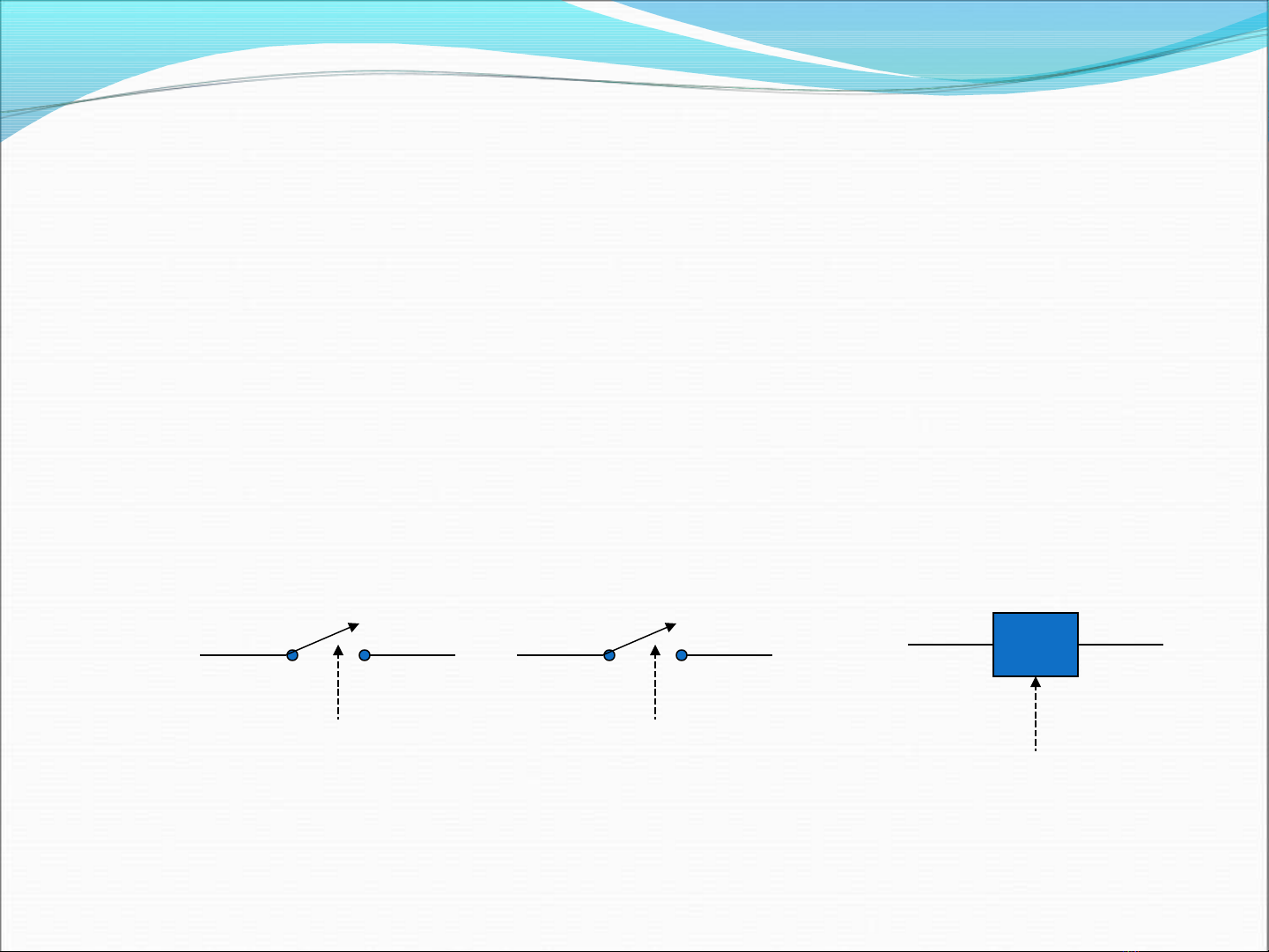
Phân t nhi phân đn gian nhât la chuyên mach co 2 ư ơ
trang tha i
Nêu môt chuyên mach đc điêu khiên b i môt biên x. ươ ơ
Ta no i răng, chuyên mach đo ng nêu x=1 va ngăt nêu
x=0
x=0 x=1 x
S
5
Khoa ĐT-VT, Đại học Bách Khoa Hà nội
Tiến sỹ Hoàng Mạnh Thắng


























