THỐNG KÊ
KINH DOANH
(Business Statistics)
Chương 4.
Đại lượng ngẫu nhiên và các
phân phối xác suất
1

IV.1. Định nghĩa và phân loại đại
lượng ngẫu nhiên
IV.2. Đại lượng ngẫu nhiên rời rạc
IV.3. Một số phân phối xác suất
thông dụng
Chương 4: ĐẠI LƯỢNG NGẪU NHIÊN VÀ
CÁC PHÂN PHỐI XÁC SUẤT
2

IV.1. ĐỊNH NGHĨA và PHÂN LOẠI
ĐẠI LƯỢNG NGẪU NHIÊN
Ví dụ mở đầu. Công ty bảo hiểm nhân thọ Metropolitan
Công ty được thành lập năm 1863, ở thời kỳ đỉnh cao
của cuộc Nội chiến Hoa Kỳ.
Mục đích ban đầu: bảo đảm dân sự cho những người
lính chiến chống lại thương tật phải chịu đựng từ chiến
tranh.
Sau khi chiến tranh kết thúc, họ đã thay đổi định hướng
và quyết định tập trung vào việc bán bảo hiểm nhân thọ.
Bảo hiểm nhân thọ là một ví dụ minh họa cho khái niệm
“đại lượng ngẫu nhiên”.
3
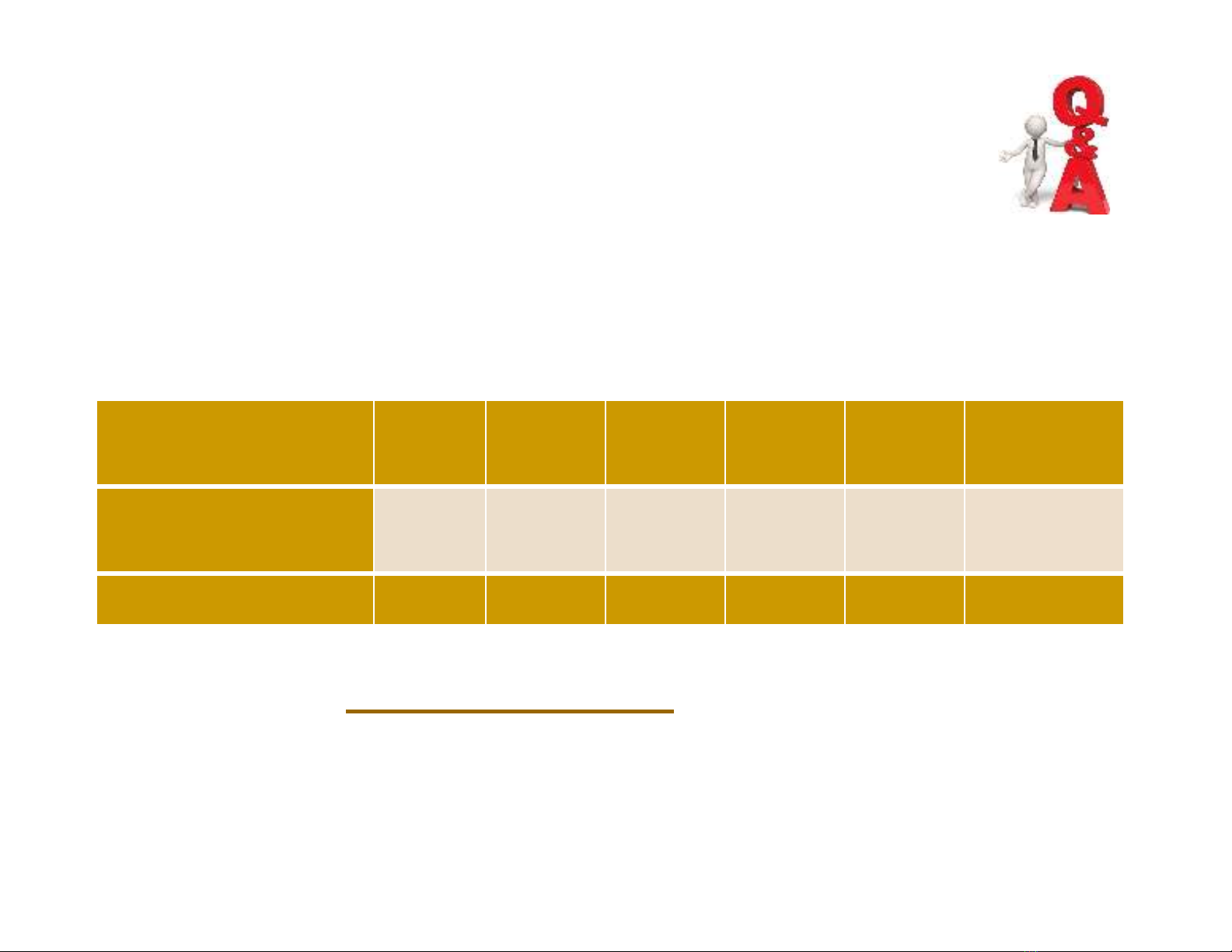
Ví dụ 4.1.Gọi Xlà số tiền bồi thường của Công ty bảo hiểm
Metropolitan trả cho những người lính bị thương tật trong
cuộc chiến. Giả sử sau đây là bảng phân phối xác suất của X:
Hãy cho biết số tiền trung bình mà mỗi người lính nhận
được khi tham gia bảo hiểm? Nếu Công ty cung cấp dịch vụ
bảo hiểm đến những người lính với giá 8000 USD/người thì
trung bình Công ty lời bao nhiêu trên mỗi hợp đồng?
Loại thương tật Chết Loại 1 Loại 2 Loại 3 Loại 4 Nhẹ hơn
X(nghìn USD) 100 50 40 30 20 0
P0,001 0,003 0,009 0,13 0,15 0,707
4
IV.1. ĐỊNH NGHĨA và PHÂN LOẠI
ĐẠI LƯỢNG NGẪU NHIÊN (ĐLNN)

1. Khái niệm
Đại lượng cho tương ứng mỗi kết quả của phép thử
với một số được gọi là đại lượng ngẫu nhiên (hay
biến ngẫu nhiên) trên các kết quả của phép thử
đó. Nói một cách khác, đại lượng ngẫu nhiên là đại
lượng có giá trị thay đổi tuỳ theo phép thử. Hay:
Định nghĩa: Đại lượng ngẫu nhiên là đại lượng
biến đổi biểu thị các giá trị kết quả của một phép
thử ngẫu nhiên.
Ta thường dùng các kí hiệu: X,Y,Z,… để biểu thị cho
đại lượng ngẫu nhiên.
5
IV.1. ĐỊNH NGHĨA và PHÂN LOẠI ĐLNN
Đại lượng (dt): cái có thể đo được, tính được
bằng cách nào đó (trong vật lí, toán học, v.v.) [*]











