Trang 1
TRƯỜNG ĐẠI HỌC VÕ TRƯỜNG TOẢN
KHOA DƯỢC

BÀI GIẢNG MÔN HỌC
THỰC TẬP VẬT LÝ 2
Giảng viên biên soạn:
Ths. LÂM VĂN NGOÁN
Đơn vị: Khoa Dược
Bộ môn: Khoa học cơ sở - cơ bản
Hậu Giang –
Năm 2015
Trang 2
Bài 1 : SỬ DỤNG THƯỚC KẸP - PANME
A/ THỰC HÀNH THƯỚC KẸP
I/ MỤC ĐÍCH
Nắm được nguyên tắc cấu tạo du xích của thước kẹp. Biết cách sử dụng
thước kẹp để đo kích thước của một số vật bằng những động tác chính xác.
II/ CƠ SỞ LÝ THUYẾT
1/ Mô tả dụng cụ và cách sử dụng
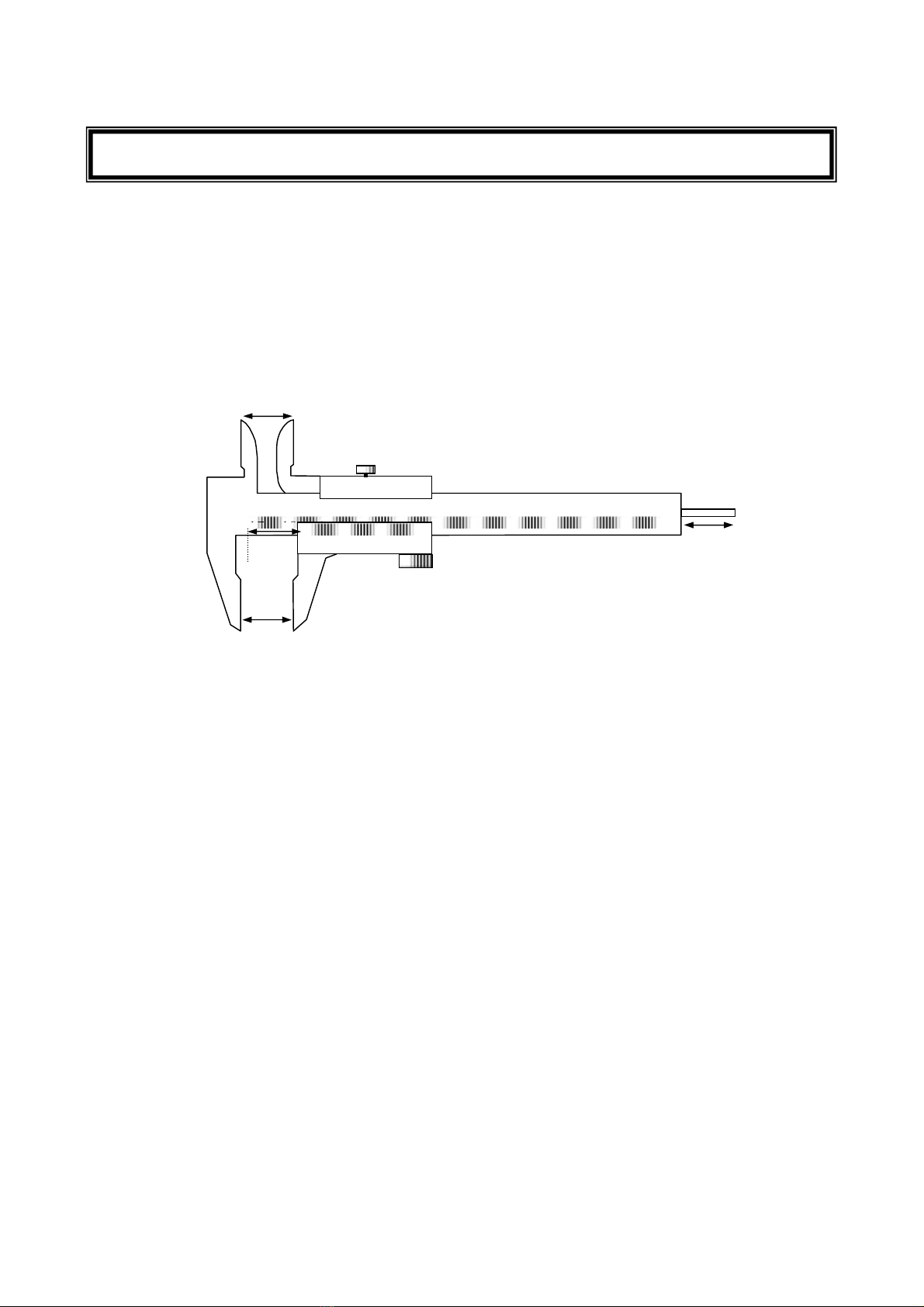
Hình 1
Thước kẹp có hai hàm A và B (Hình 1). Hàm A đứng yên gắn liền với thước
thường L1. Hàm B chuyển động dọc theo chiều dài của thước L1, gắn liền với một
thước nhỏ L2 gọi là du xích (thước chạy). Thước L1 chia đến mm và đánh số từng
cm (1; 2; 3cm…). Khi hai hàm khít nhau, vạch 0 của L1 trùng với vạch 0 của du
xích L2.
Khi hai hàm A và B cách nhau một khoảng d thì khoảng ấy bằng chiều dài từ
điểm 0 của thước thường đến điểm 0 của du xích (Hình 1.1).
Muốn đo kích thước của một vật, ta đặt vật đó giữa hàm A và B và khẽ đẩy
hàm B sát vào vật. Lúc ấy ốc D được mở lỏng. Để đảm bảo hai hàm A và B kẹp
chặt vật mà không làm biến dạng vật, ta cho hàm B tiến khít đến vật một cách nhẹ
nhàng và vặn ốc C từ từ. Khi nào việc xoay ốc C không nhẹ nhàng như trước nữa
tức là vật đã bị kẹp chặt giữa hai hàm A và B. Khi muốn lấy vật ra khỏi hàm A và B
ta lại xoay ốc ngược chiều với trước để kéo hai hàm ra xa vật.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
17 18 19 20
0 1 2 3 4 5 6 7
L
L2
E
D
d
d
d
A B
Trang 3
Để đọc kết quả đo bằng thước kẹp, ta phải nắm được nguyên tắc cấu tạo du
xích của thước kẹp.
2/ Nguyên tắc cấu tạo của du xích
Trên thước L1 lấy một đoạn a mm chia làm b khoảng. Mỗi khoảng dài
b
amm.
Trên du xích L2 lấy một đoạn dài (a-1) chia làm b khoảng. Mỗi khoảng dài
b
a1
mm.
Vậy mỗi khoảng của du xích ngắn hơn mỗi khoảng của thước thường là:
b
a mm -
b
a1
mm =
b
1mm.
b
1
mm là đại lượng đặc trưng cho du xích.
Dựa vào giá trị của
, ta phân loại các du xích:
- Du xích 02,0 mm tức có 02,0
mm.
- Du xích 05,0 mm tức có 05,0
mm.
- Du xích 0,1mm tức có 1,0
mm.
Ví dụ: Ta dùng thước kẹp có du xích 1,0 mm. Cấu tạo du xích này như sau:
Trên thước thường L1 lấy một đoạn a = 10mm chia làm b = 10 khoảng. Mỗi
khoảng dài 1
b
amm. Trên du xích L2 lấy một đoạn dài (a-1) = 9mm chia làm b = 10
khoảng. Mỗi khoảng dài 9,0
1
b
amm. Vậy mỗi khoảng của du xích ngắn hơn mỗi
khoảng của thước thường là:
1
mm - 9,0 mm = 0,1mm.
Nếu xét n khoảng của du xích và n khoảng của thước thường (mỗi khoảng
dài 1mm) thì n khoảng của du xích ngắn hơn:
nn 1,0
mm
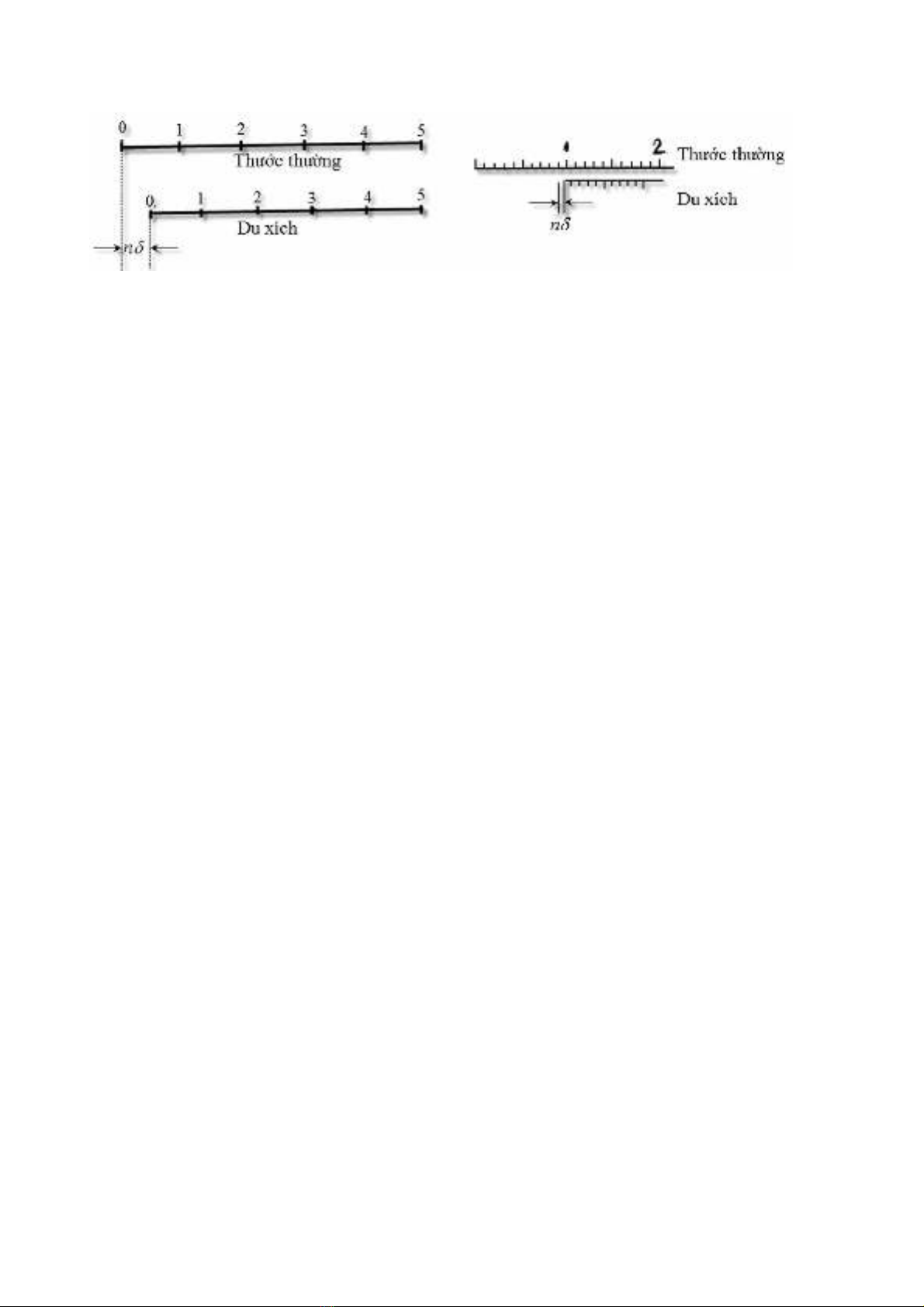
Chẳng hạn như theo hình 1.2, số 5 của du xích trùng với số 5 của thước
thường (n=5) nên khoảng của du xích sẽ ngắn hơn: 5,01,0
nmm.
Trang 4
Hình 2 Hình 3
3/ Cách đọc kết quả:
Như ta đã nói ở trên, muốn đo vật, ta kẹp chặt vật giữa hai hàm A và B.
Khoảng cách giữa hai hàm A và B là kích thước của vật bằng khoảng cách d giữa
vạch 0 của thước thường L1 và vạch 0 của du xích L2.
Chẳng hạn theo hình 1.3 ta có d = 9mm +
n (9mm là phần nguyên tính từ
vạch 0 của thước thường đến vạch gần vạch 0 của du xích về phía bên trái). Để
tính
n, ta tìm trên du xích và trên thước thường hai vạch nào trùng nhau. Giả sử
vạch số 6 (n=6) của du xích trùng với vạch 15mm của thước thường. Vậy đối với
du xích kể từ vạch trùng (vạch 6) đến vạch 0 của du xích có 6 khoảng, còn đối với
thước thường kể từ vạch trùng (vạch 15) đến vạch 9mm có (15-9)/1=6 khoảng.
Như vậy, 6 khoảng này dài hơn 6 khoảng của du xích một đoạn
n.
n6,06.1,0
mm.
Khi đó: d = 9mm + 0,6mm = 9,6mm.
Như vậy, do cấu tạo của thước kẹp có du xích 1,0 mm, ta đưa ra cách đọc
đơn giản:
d = 9mm +
n
n: số thứ tự vạch trên du xích trùng với vạch bất kỳ trên thước thường.
Ví dụ: vạch thứ 8 trên du xích trùng với vạch bất kỳ trên thước thường.
9
dmm+8.0,1mm=9,8mm.
Tóm lại, cách đọc kết quả đo kích thước của vật khi sử dụng thước kẹp được
phát biểu như sau:
+ Phần nguyên (phần mm) đọc trên thước thường, vạch ở phía trái và gần
vạch 0 của du xích nhất.
+ Phần thập phân đọc trên du xích, vạch trùng với một vạch bất kỳ trên thước
thường (
n).
Trang 5
+ Kết quả của phép đo là tổng hai kết quả trên.
III/ THỰC HÀNH
1/ Hiệu chỉnh số 0
Nếu hai hàm A và B khít nhau mà số 0 của du xích nằm ở phía bên phải số 0
của thước thường thì kích thước của vật bằng kết quả đọc được trừ đi khoảng
cách giữa hai số 0.
Nếu hai hàm A và B khít nhau, mà số 0 của du xích nằm ở phía bên trái số 0
của thước thường thì kết quả đọc được phải cộng thêm khoảng cách giữa hai số 0
khi hai hàm khít nhau.
2/ Thực hành đo
Đo đường kính trong (d1), đường kính ngoài (d2) của một hình trụ rỗng. Mỗi
đường kính đo 3 lần tại các vị trí khác nhau. Lập bảng 1.
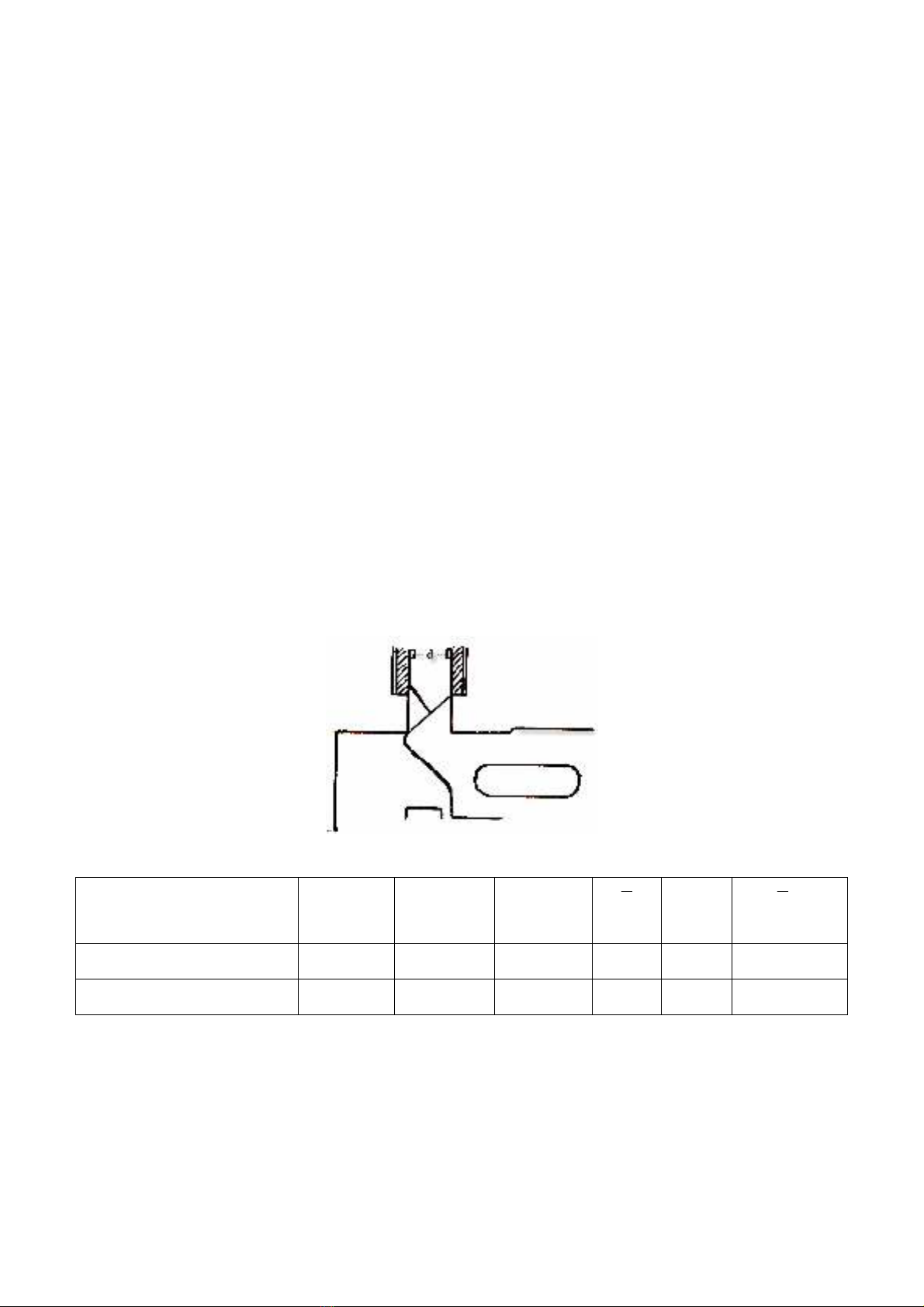
Chú ý: Để đo đường kính trong của hình trụ, ta đặt thước kẹp như hình 1.4.
Đường kính trong vẫn bằng khoảng cách từ số 0 của thước thường đến số 0 của
du xích.
Hình 4
Kích thước cần đo
(mm)
Đo lần 1
Đo lần 2 Đo lần 3
d d
d = dd
Đường kính trong (d1)
Đường kính ngoài (d2)
Bảng 1