CH NG 9:ƯƠ
TÍNH TOÁN H CH A ĐI U TI T Ồ Ứ Ề Ế
C P N CẤ ƯỚ
I. Khái ni m chungệ
H ch a đi u ti t năm (mùa) là h ch a có ồ ứ ề ế ồ ứ
nhi m v tích l ng n c th a c a các th i ệ ụ ượ ướ ừ ủ ờ
kỳ th a n c đ c p b sung cho các th i ừ ướ ể ấ ổ ờ
kỳ thi u n c, chu kỳ ho t đ ng là m t ế ướ ạ ộ ộ
năm.
H ch a đi u ti t m t l nồ ứ ề ế ộ ầ
H ch a đi u ti t hai hay nhi u l n đ c l pồ ứ ề ế ề ầ ộ ậ
H ch a đi u ti t hai hay nhi u l n không ồ ứ ề ế ề ầ
đ c l pộ ậ
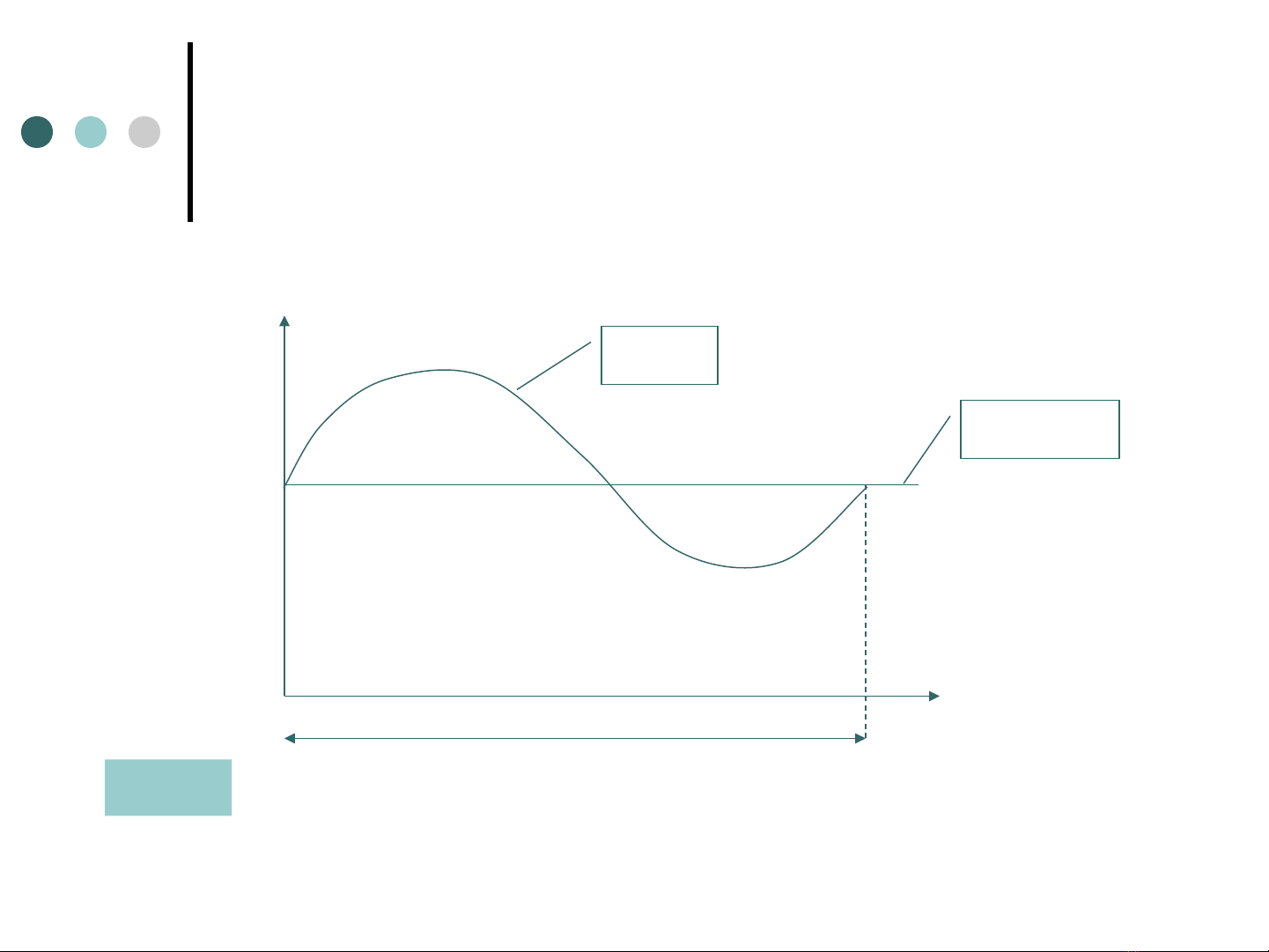
Đi u ti t m t l nề ế ộ ầ
Q,q
(m3/s)
t
T=1năm
V+
V-
Q~t
q=const
Vh=V-
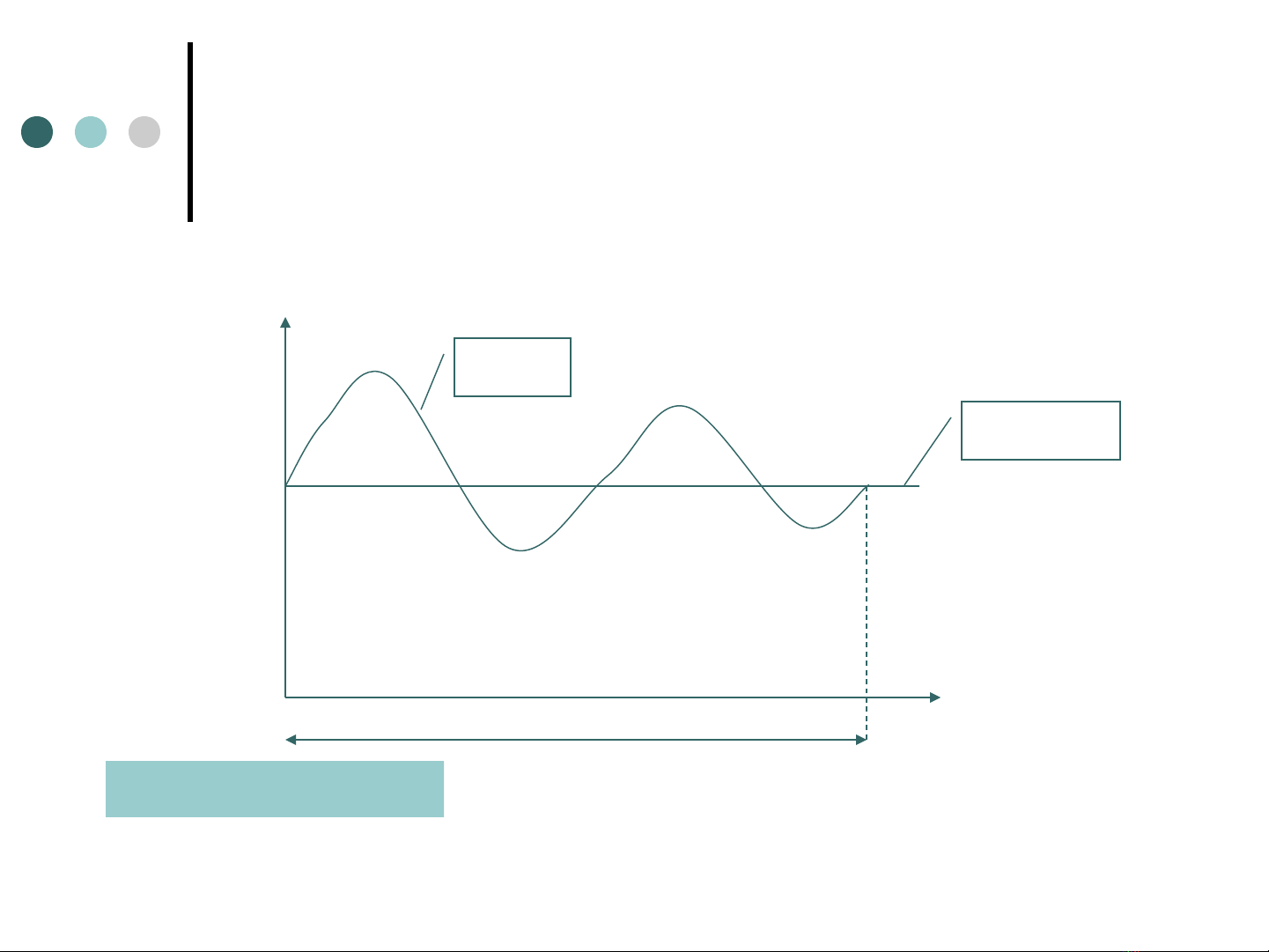
Đi u ti t hai l n đ c l pề ế ầ ộ ậ
Q,q
(m3/s)
t
T=1năm
V1+
Q~t
q=const
V2+
V1- V2-
Vh=max(V1-,V2-)
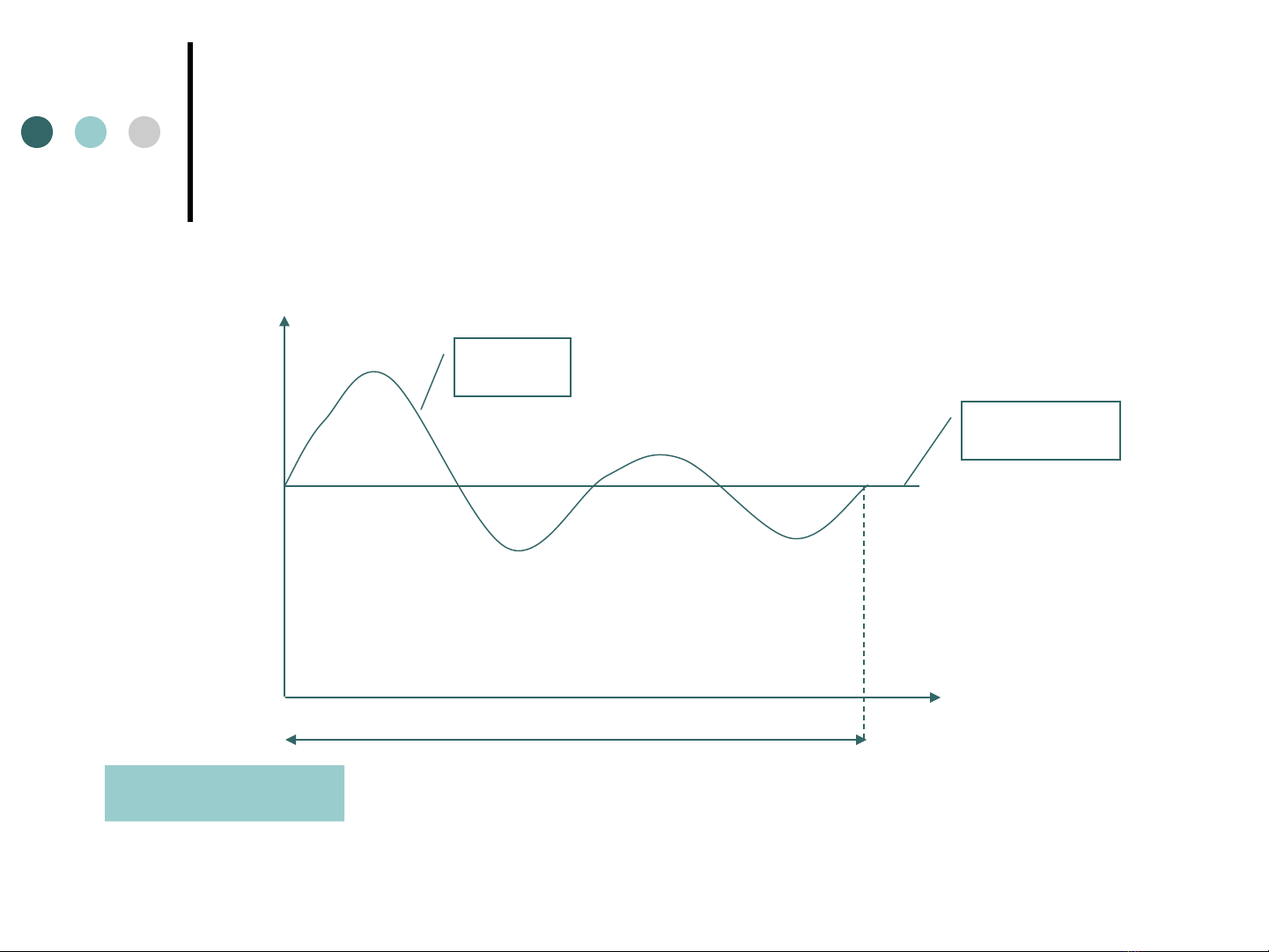
Đi u ti t hai l n không đ c ề ế ầ ộ
l pậ
Q,q
(m3/s)
t
T=1năm
V1+
Q~t
q=const
V2+
V1- V2-
Vh=V1-+V2—V2+