Môn họcMôn học
TÍN HIỆU VÀ HỆ THỐNGTÍN HIỆU VÀ HỆ THỐNG
Giảng viên: PGS. TS. Huỳnh Thái Hoàng
Khoa Điện – Điện Tử
Đại học Bách Khoa TPHCM
Email: hthoang@hcmut edu vn
Email:
hthoang@hcmut
.
edu
.
vn
Homepage: www4.hcmut.edu.vn/~hthoang/
1
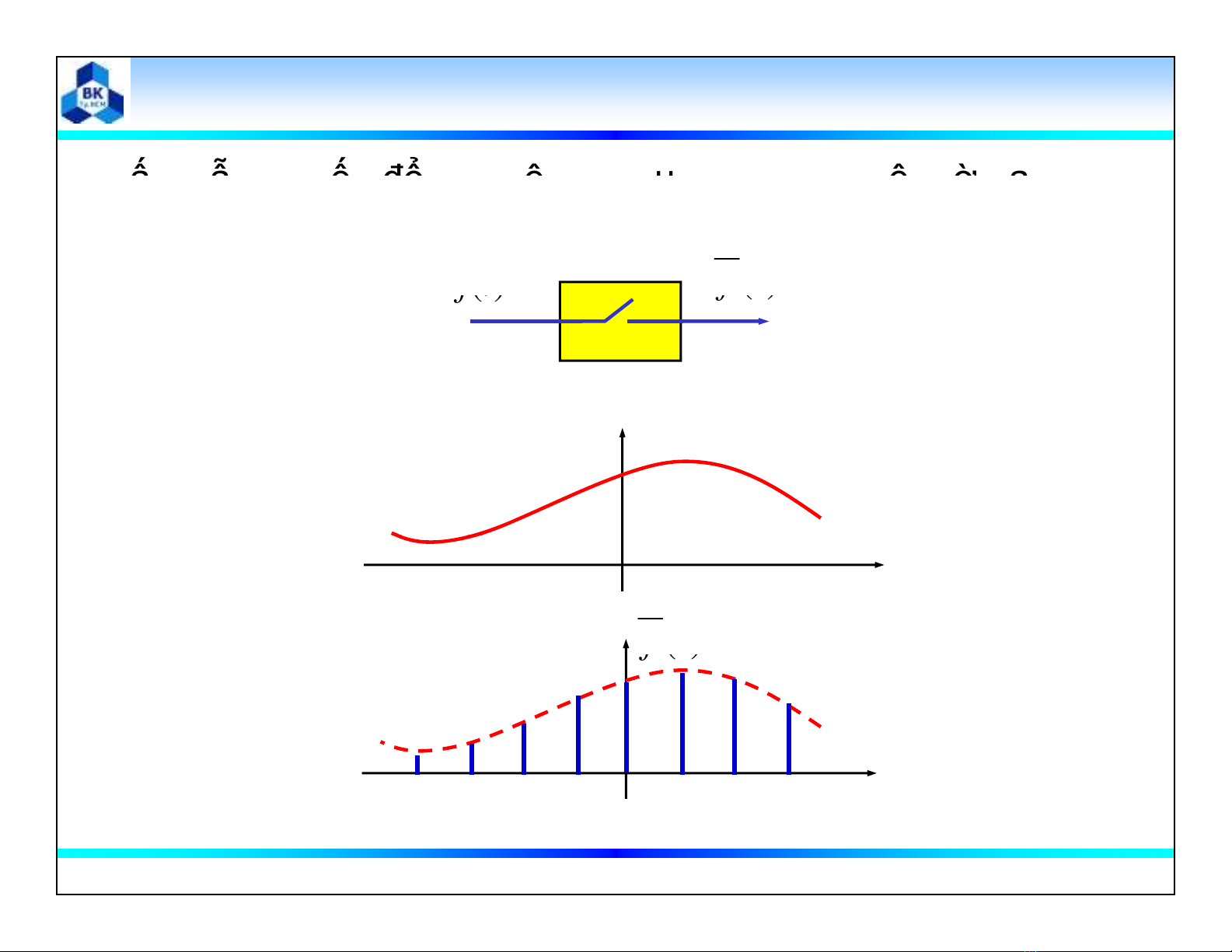
Bài giảng Tín hiệu và hệ thống: Chương 7 - Lấy mẫu tín hiệu giới thiệu về lý thuyết lấy mẫu, biến đổi Fourier rời rạc (DFT), biến đổi Fourier nhanh (FFT). Mời các bạn cùng tham khảo!