Tran Quang Viet – FEEE – HCMUT
Signals and Systems --HK153--
Hệ thống tuyến tính bất biến (LTI) & tích chập
Lecture 3
EE 2005: Tín hiệu và hệ thống
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT
Signals and Systems --HK153--
Hệ thống LTI
Hệ thống LTI: HT thỏa mãn tính tuyến tính & bất biến
Môn học này tập trung khảo sát hệ thống LTI vì:
Phần lớn các hệ thống vật lý trên thực tế đều là hệ
thống LTI
Một số hệ thống là phi tuyến nhưng trong một giới
hạn nào đó người ta sẽ tương đương nó là LTI để khảo
sát vì ngõ ra của hệ thống LTI sẽ dễ dàng xác định
thông qua phương pháp “biểu diễn” tín hiệu
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT
Signals and Systems --HK153--
Biểu diễn tín hiệu cho hệ thống LTI
Tín hiệu k(t), k=1,2,….n được gọi là tín hiệu cơ bản khi
cấp nó vào ngõ vào của hệ thống LTI thì ngõ ra đã được
xác định
Để xác định ngõ ra của hệ thống LTI với một ngõ vào bất
kỳ nào đó ta tìm cách “biểu diễn” nó thành tổ hợp tuyến
tính của k(t) hoặc k(t-t0) khi đó tính chất bất biến và xếp
chồng dễ dàng được sử dụng
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT
Signals and Systems --HK153--
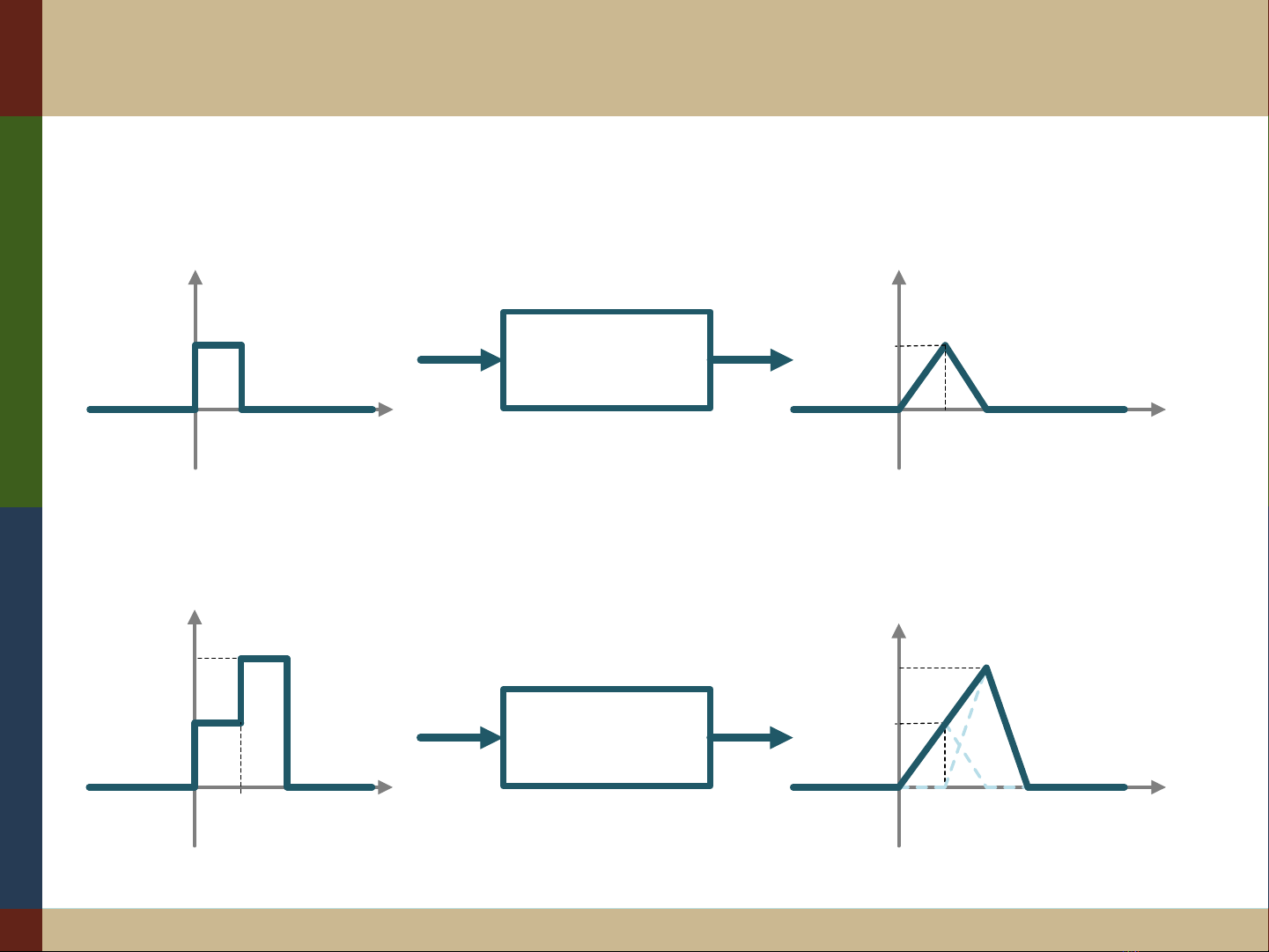
Biểu diễn tín hiệu cho hệ thống LTI
Ví dụ: (t) là ngõ vào hệ thống LTI và ngõ ra là (t)
0
1
t (s)
(t)
2
Hệ thống
(LTI)
0
1
t (s)
(t)
24
Khi đó: f(t) là ngõ vào hệ thống LTI và ngõ ra là y(t)
0
1
t (s)
f(t)
2
Hệ thống
(LTI)
0
1
t (s)
y(t)
24
4
22
6
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT
Signals and Systems --HK153--
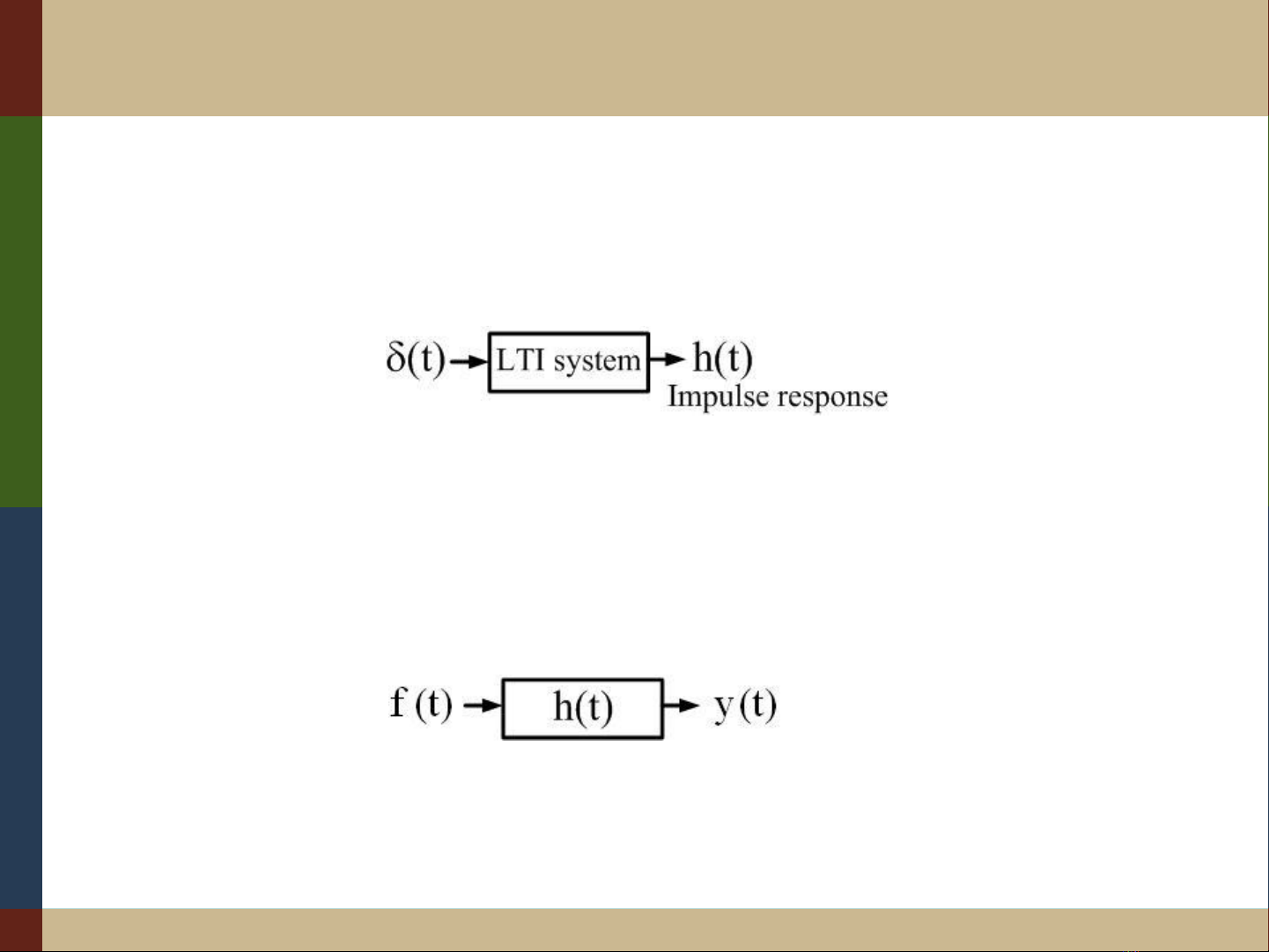
Đáp ứng xung của hệ thống LTI
Cấp xung đơn vị (t) vào ngõ vào của hệ thống LTI, khi
đó ngõ ra của hệ thống gọi là đáp ứng xung, ký hiệu h(t)
Ví dụ: y(t)=f(t-1) h(t)=(t-1)
h(t) mô tả cho đặc tính của hệ thống LTI: