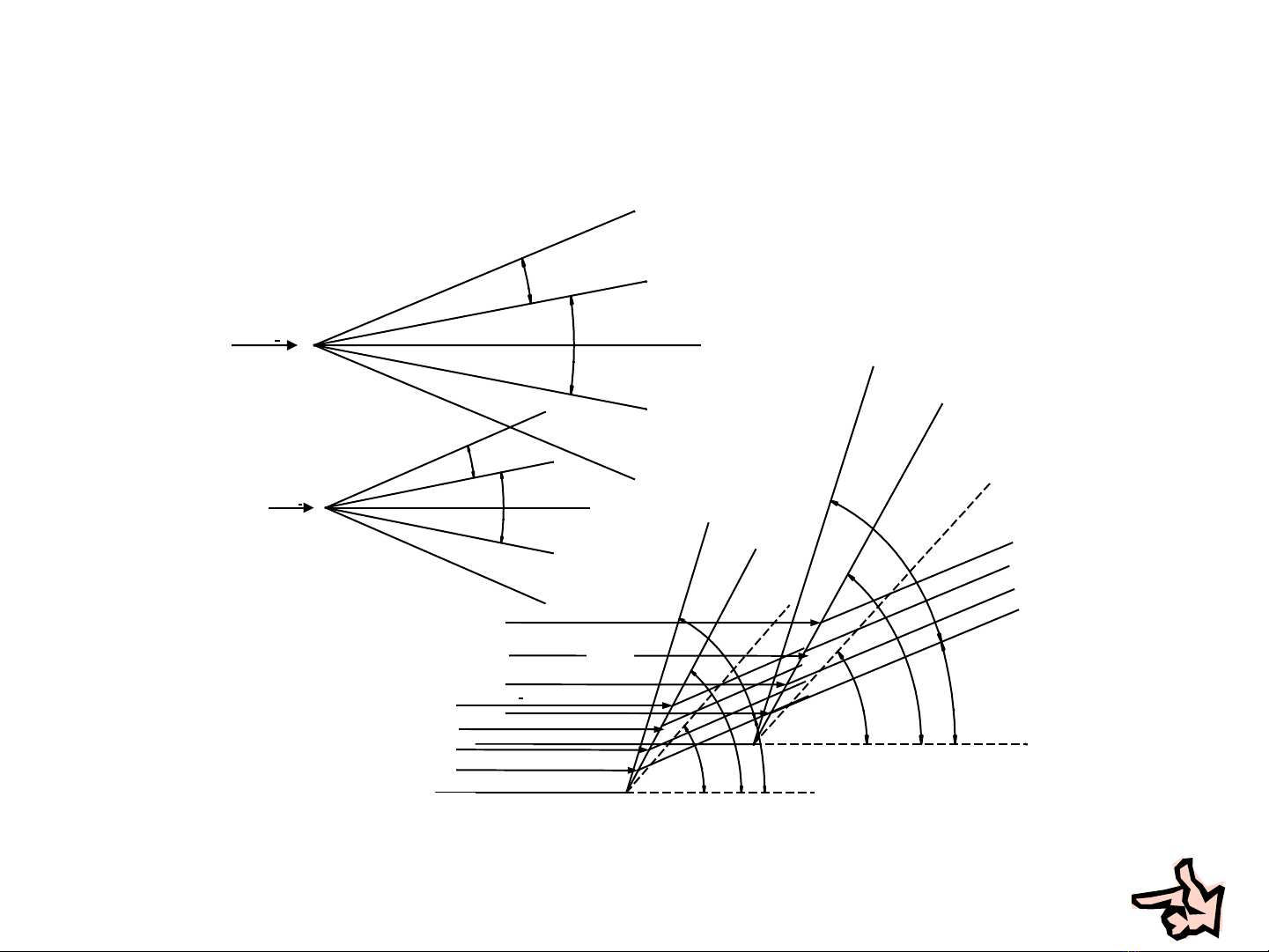
Trên c s các k t qu tìm đc đi v i tr ng h p tăng v t nén th ng ta suy ra cho ơ ở ế ả ượ ố ớ ườ ợ ọ ẳ
tr ng h p tăng v t nén xiên. Nh ng đây dòng ch y s thay đi ph ng sau khi qua m t tăng ườ ợ ọ ư ở ả ẽ ổ ươ ặ
v t nén xiên; dòng s l ch đi m t góc.ọ ẽ ệ ộ
D
V2
C1
c
C2
b)
B
Hình 9-11
c
C2
A
b)
a)
B
Hình 9-11
v1
v1
v1
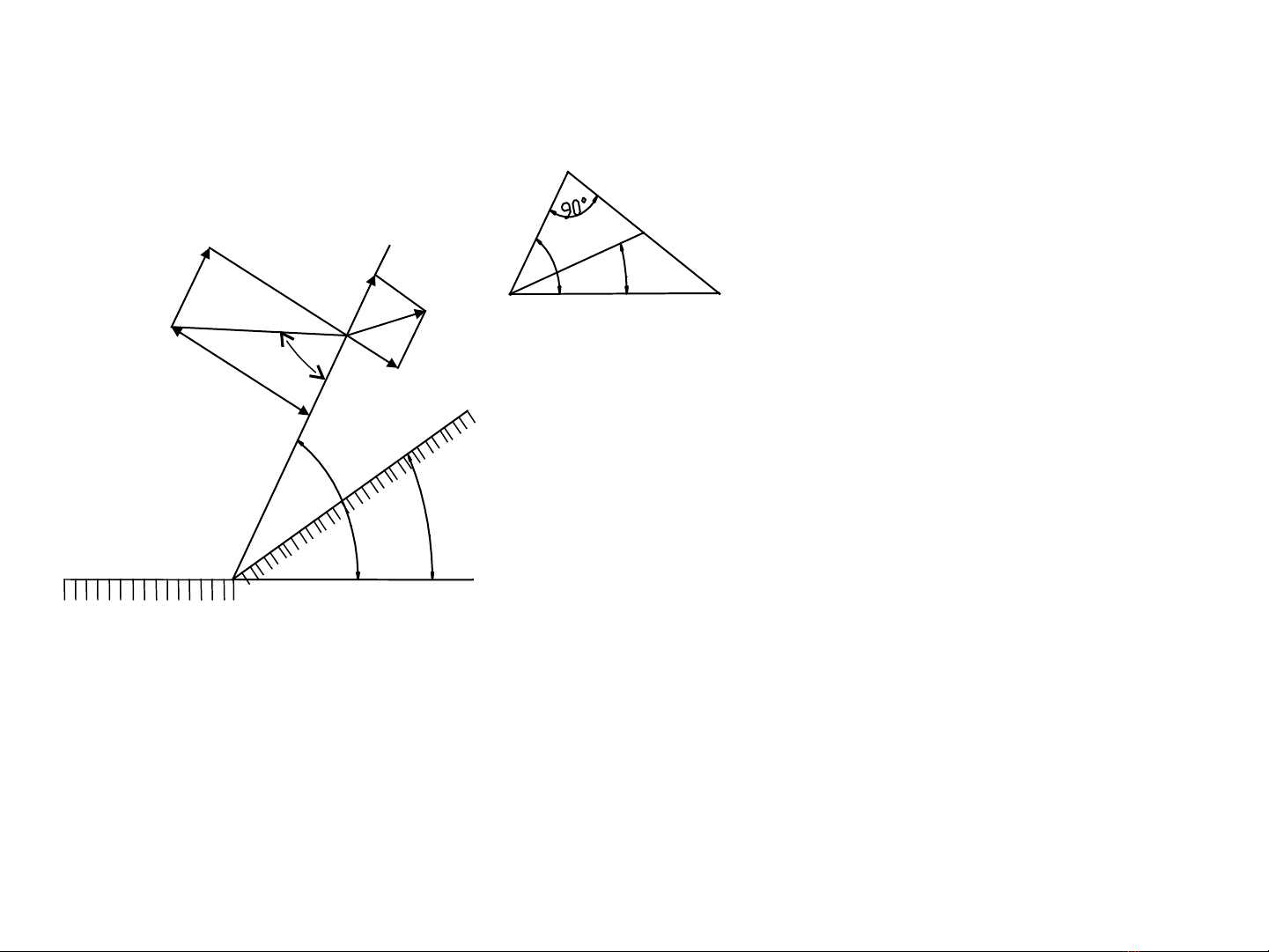
1. H th c đng h c c b nệ ứ ộ ọ ơ ả
Ta s ch ng minh (hình ẽ ứ
9-12)
Đ ch ng minh ta áp ể ứ
d ng đnh lý bi n thiên ụ ị ế
đng l ng cho kh i khí ộ ượ ố
ữ ậ
nn
tt
vv
constvv
12
21
tttt
vvvvpppp
2221112121
)()(
v2n
vt
v1
v2
v1t
v1n
v2
v2t
v2n
v1
Hình 9-12

1. H th c đng h c c b nệ ứ ộ ọ ơ ả
K t h p v i ph ng trình liên t c: ế ợ ớ ươ ụ
ta đc:ượ
suy ra:
Chi u lên ph ng pháp tuy n:ế ươ ế
Vì nên suy ra:
.
Nh v y đi v i tăng v t nén xiên s đt bi n v v n t c ư ậ ố ớ ọ ự ộ ế ề ậ ố
0)( 2111 ttt vvv
tt
vv
2211
constvv
tt
21
)(
211112 nnn
vvvpp
12
pp nn vv 21
n
v1
n
v
2
2
*21 nnn
avv

1. H th c đng h c c b nệ ứ ộ ọ ơ ả
1
21
.
*
2
*
1
nn
a
v
a
v
n
n
n
n
g2
v
A
TC
A
TC
g2
v
A
TC
g2
v
2
t
0p2p
2
n2
1p
2
n1
2
0
2
22
2
110
222
t
p
n
p
n
p
n
v
gC
A
Tv
gC
A
Tv
gC
A
TT
hay là:
trong đó - v n t c âm t i h n pháp tuy n.ậ ố ớ ạ ế
Có th bi u di u h th c đng h c (9-19) qua v n ể ể ễ ệ ứ ộ ọ ậ
t c âm t i h n toàn ph n a* và thành ph n v n t c ố ớ ạ ầ ầ ậ ố
ti p tuy n. Mu n th ta vi t ph ng trình nhi t hàm ế ế ố ể ế ươ ệ
ướ ạ
n
a
*

1. H th c đng h c c b nệ ứ ộ ọ ơ ả
đây đc g i là nhi t đ hãm đi v i thành ph n Ở ượ ọ ệ ộ ố ớ ầ
v n t c pháp tuy n. T ng t nh trong tăng v t nén ậ ố ế ươ ự ư ọ
th ng ta cũng có các công th c (9-9) và (9-10).ẳ ứ
(9-20b)
Thay (9-20b) vào (9-20a) v i chú ý AR = ta s ớ ẽ
đc h th c đng h c:ượ ệ ứ ộ ọ
n
T0
n1n2
12
12
vv
pp
2
n*n0
12
12
agRT
1k
k2pp
k
k
Cp 1
22
*21
1
1
tnn
v
k
k
avv


![Chương trình khung trình độ cao đẳng nghề Cắt gọt kim loại - Trường CĐN KTCN Dung Quất [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2021/20210417/tradaviahe20/135x160/1301618651048.jpg)
![Tổng hợp 58 câu hỏi về đồ án Chi tiết máy [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2020/20201015/daohachi0512/135x160/9011602770055.jpg)









![Bài giảng Vẽ kỹ thuật cơ khí: Chương 2 - Trường ĐH SPKT (ĐH Đà Nẵng) [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260303/zinedinezidane06/135x160/64351772685568.jpg)












