
Bài giảng môn Toán 9
§ 5. CÔNG THỨC NGHIỆM THU GỌN
Tiết 55
I. CÔNG THỨC NGHIỆM THU GỌN
2
2 2
2
Δ = - 4 = (2 ') 4
= ( ' 4 ' 4 4 )
b ac b ac
bb acac
Kí hiệu Δ’ = b’2 – ac ta có Δ = 4 Δ’
Cho phương trình
ax2 + bx + c = 0 (a 0)
Đặt b = 2b’, hãy tính biệt
thức Δ theo b’,a,c.
Dựa vào công thức
nghiệm đã học, b = 2b’và
Δ = 4 Δ’ hãy tìm nghiệm
của phương trình (nếu có)
ứng với các trường hợp
Δ’>0, Δ’ = 0, Δ’ < 0
§ 5. CÔNG THỨC NGHIỆM THU GỌN
Tiết 55
Hãy thực hiện yêu cầu trên bằng cách hoàn thành phiếu học tập sau:
PHIẾU HỌC TẬP
Điền vào các chỗ trống (…) để được kết quả đúng:
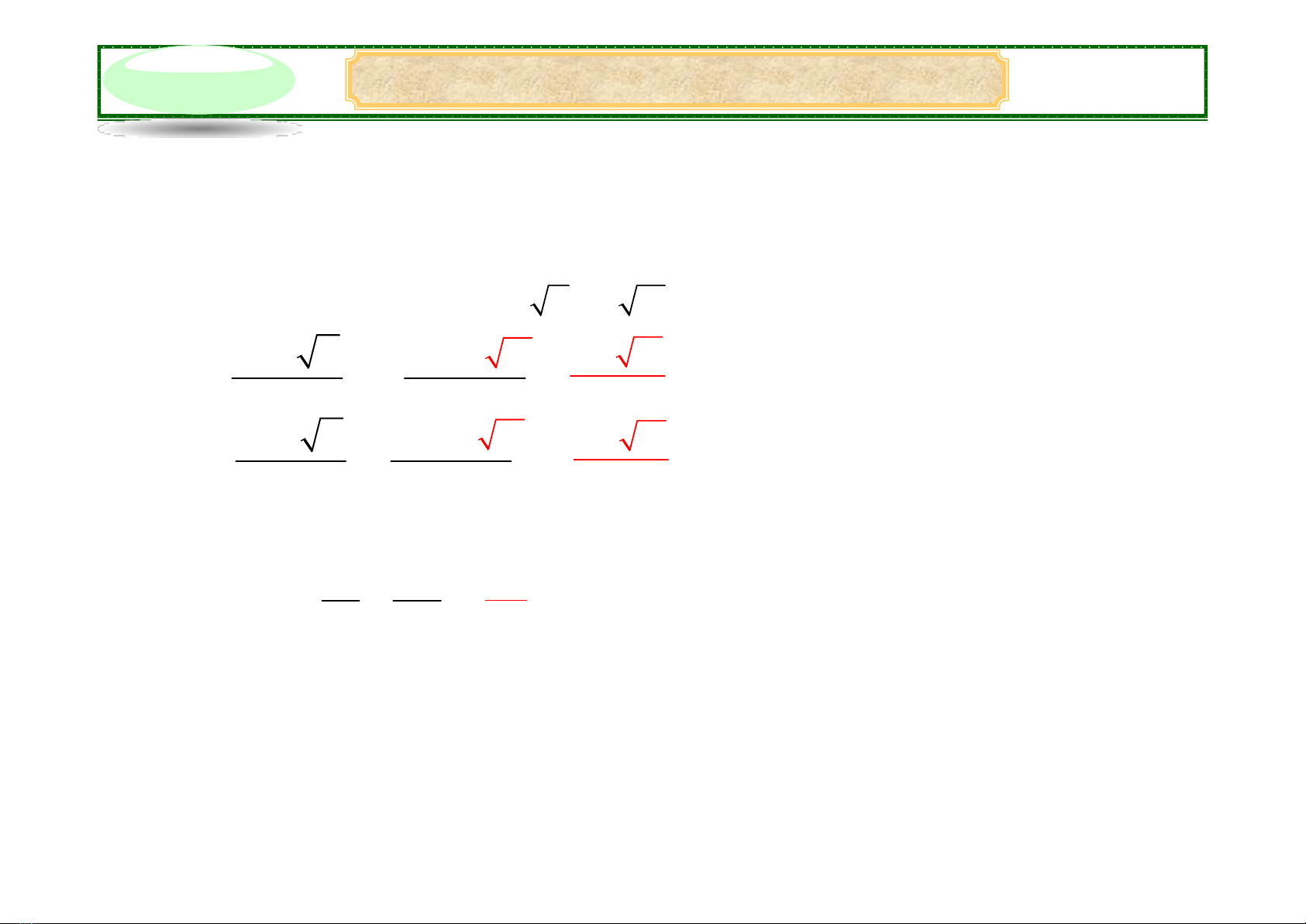
+ Nếu Δ’ > 0 thì Δ …0 (khi đó ),phương trình có ………………….…….
... '
1
..... .......
..................
2 2
b
x
a a
2
..... .......
..................
2 2
b
x
a a
+ Nếu Δ’ = 0 thì Δ …0, phương trình có …………….
1 2
...... ..........
2 2
b
x x
a a
+ Nếu Δ’ < 0 thì Δ …0, phương trình ……………
2 '
2 'b
' 'b
a
' 'b
a
2 'b
2 '
hai nghiệm phân biệt
nghiệm kép
vô nghiệm
>
<
=
2 'b
'b
a
2
§ 5. CÔNG THỨC NGHIỆM THU GỌN
Tiết 55
1. CÔNG THỨC NGHIỆM THU GỌN
b' '
a
x1 =
b' '
a
x2 =
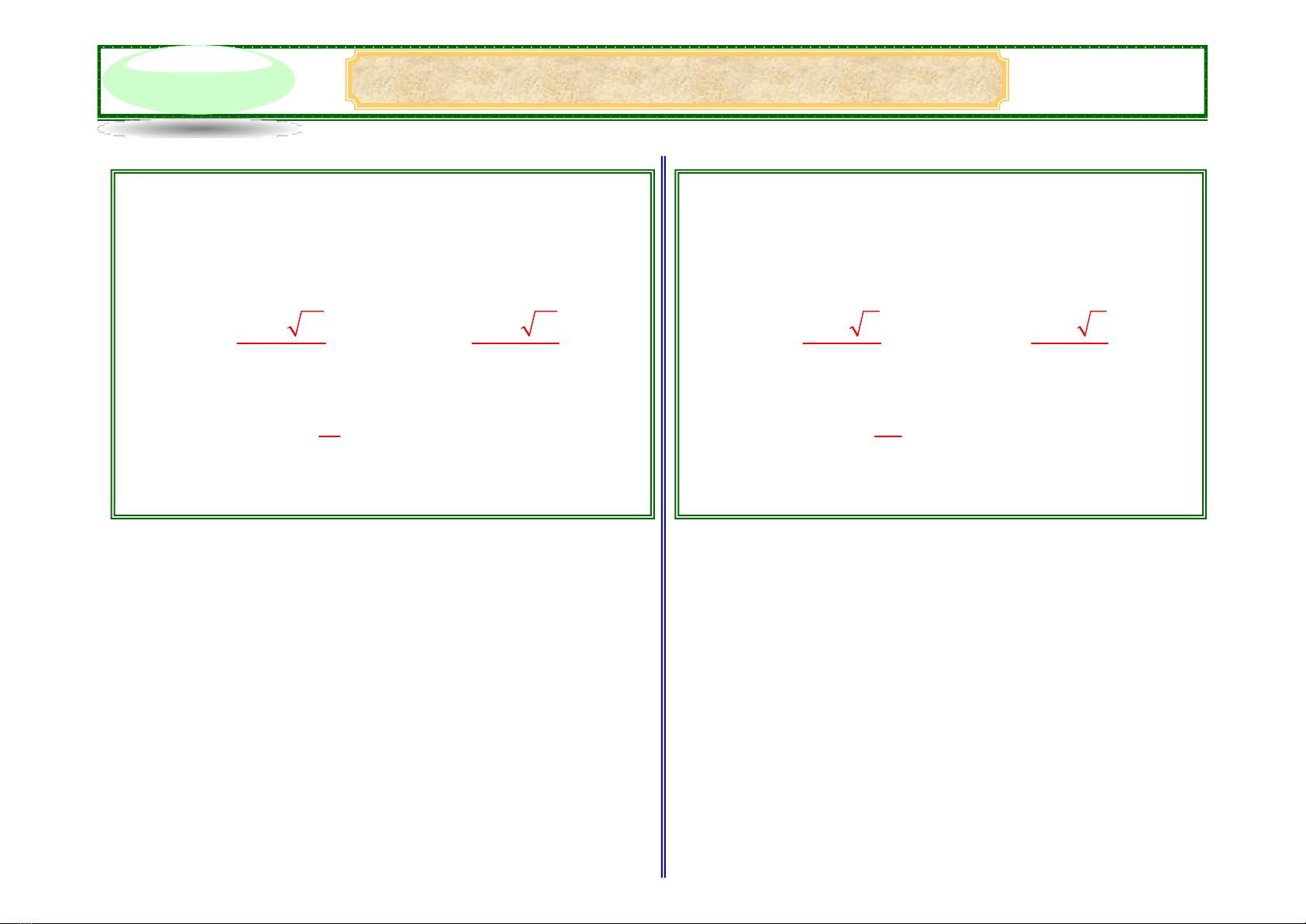
+ Nếu ∆’ > 0 thì phương trình có hai nghiệm phân biệt:
+ Nếu ∆’ = 0 thì phương trình có nghiệm kép:
+ Nếu ∆’ < 0 thì phương trình vô nghiệm.
x1 = x2 =
b'
a
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0)
và b = 2b’, Δ’ = b’2 – ac :
b
2a
x1 =
b
2a
x2 =
+ Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt:
+ Nếu ∆ = 0 thì phương trình có nghiệm kép:
+ Nếu ∆ < 0 thì phương trình vô nghiệm.
x1 = x2 =
b
2a
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0)
và Δ = b2 – 4ac :
CÔNG THỨC NGHIỆM
Các bước giải phương trình bậc hai bằng
công thức nghiệm thu gọn:
1. Xác định các hệ số a, b’ và c.
2. Tính ∆’ = b’2 – ac.
3. Nếu ∆’ > 0 hoặc ∆’ = 0 thì viết nghiệm
theo công thức.
Nếu ∆’ < 0 thì phương trình vô nghiệm.
c = . . . .
§ 5. CÔNG THỨC NGHIỆM THU GỌN
Tiết 55
1. CÔNG THỨC NGHIỆM THU GỌN
b' '
a
x1 =
b' '
a
x2 =
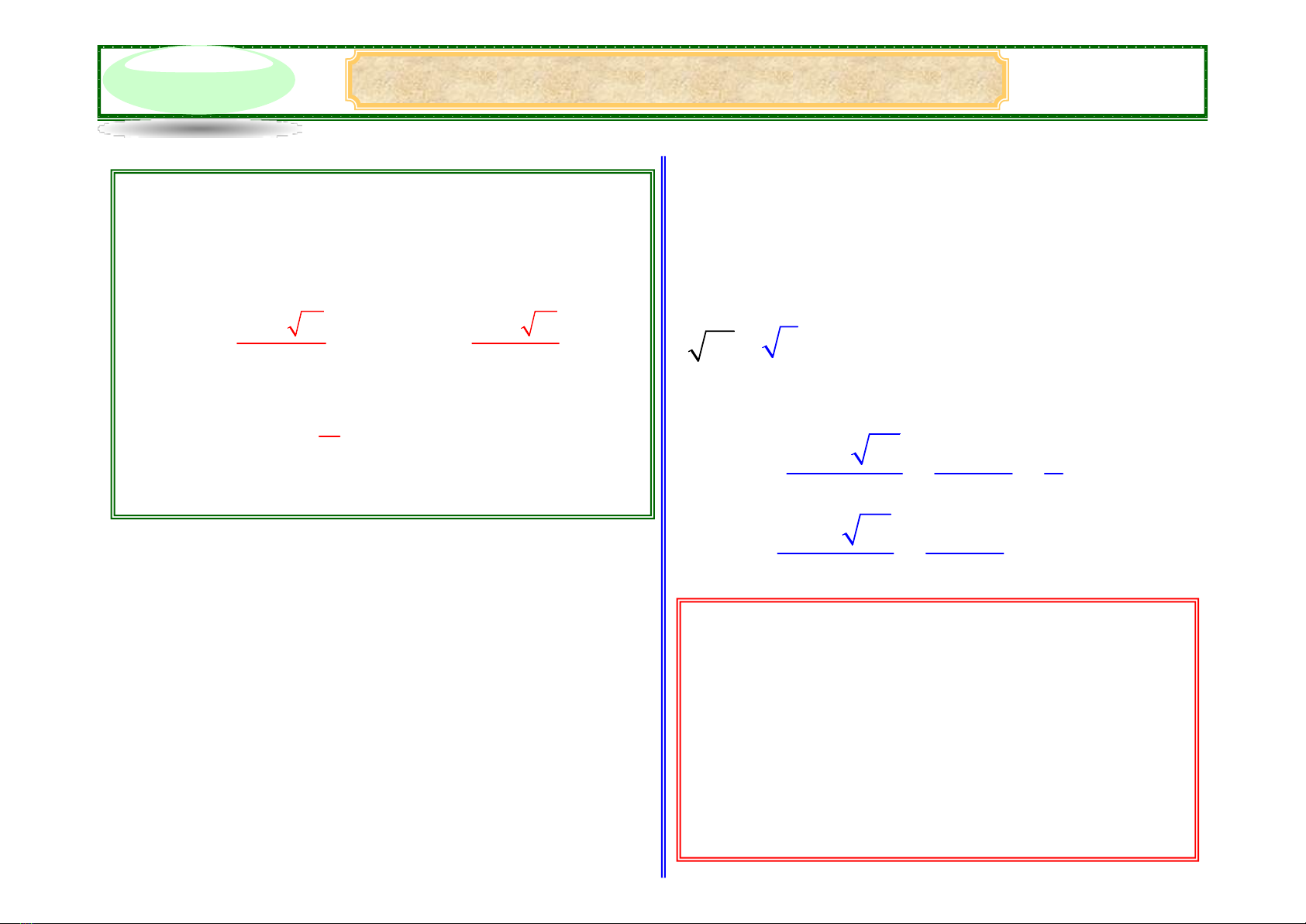
+ Nếu ∆’ > 0 thì phương trình có hai nghiệm phân biệt:
+ Nếu ∆’ = 0 thì phương trình có nghiệm kép:
+ Nếu ∆’ < 0 thì phương trình vô nghiệm.
x1 = x2 =
b'
a
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0)
và b = 2b’, Δ’ = b’2 – ac :
2. ÁP DỤNG
?2. Giải phương trình 5x2 + 4x – 1 = 0
bằng cách điền vào những chỗ trống:
a = . . . b’ = . . .
52 -1
;;
9 3
Nghiệm của phương trình:
x1 =
x2 =
b' Δ' 2 3 1
a 5 5
b' Δ' 2 3 1
a 5
Ta c
Ta có
ó :
:
Δ’ = . . .
b’2 - ac =22 – 5.(-1)= 4 + 5 = 9
' .......


























