
§ 2: Đå thÞ hµm sè
20y ax a
Tiết 49
Kiểm tra bài cũ:
HS1: Nhắc lại tính chất của hàm số y = ax² ( a 0).
x -3 -2 -1 0 1 2 3
y = 2x²
x -4 -2 -1 0 1 2 4
y=f(x)= - x²-8 -2 0 -2 -8
18 8 02 8 182
2
1
1
2
1
2
Hãy điền vào ô trống các giá trị tương ứng
của y trong bảng sau:
HS2: Nhắc lại nhận xét của hàm số y = ax² ( a 0).
Hãy điền vào ô trống các giá trị tương ứng
của y trong bảng sau:

Bảng một số cặp giá trị tương ứng của x và y
Trên mặt phẳng toạ độ lấy các điểm:
A(- 3; 18), B(- 2; 8), C(- 1; 2), O(0; 0),
A’(3; 18), B’(2; 8), C’(1; 2)
x - 3 - 2 - 1 0 1 2 3
y = 2x218 8 2 0 2 8 18
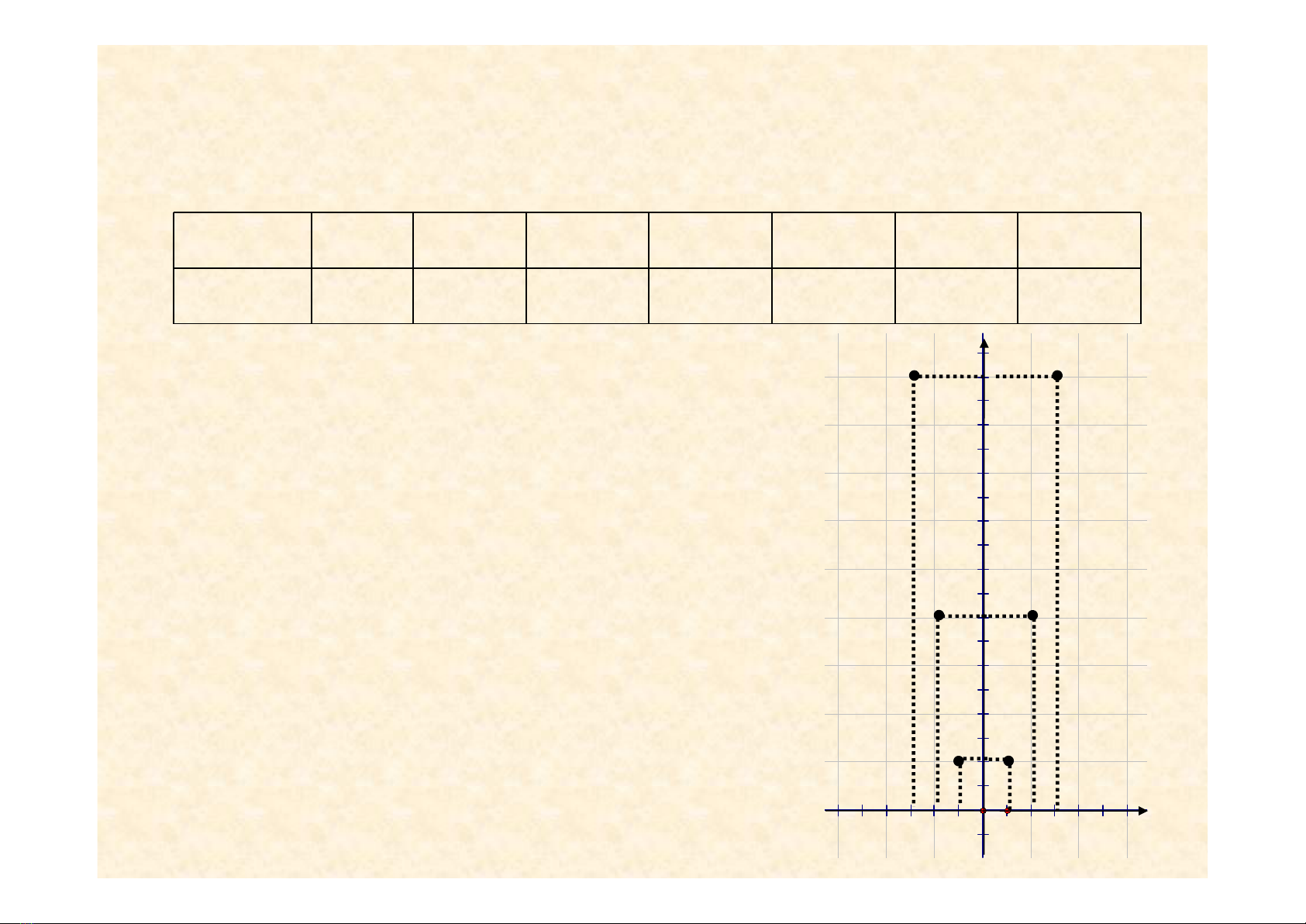
Ví dụ 1: Đồ thị hàm số y = 2x2
§ 2 : Đồ thị hàm số y = ax2 (a ≠ 0)
18
16
14
12
10
8
6
4
2
-15 -10 -5 5 10 15
0321- 1- 2-3
x
y
Ví dụ 1: Đồ thị hàm số y = 2x2
Bảng một số cặp giá trị tương ứng của x và y
x - 3 - 2 - 1 0 1 2 3
y = 2x218 8 2 0 2 8 18
Trên mặt phẳng toạ độ lấy các điểm:
A(- 3; 18), B(- 2; 8), C(- 1; 2), O(0; 0),
A’(3; 18), B’(2; 8), C’(1; 2)
C
A’
A
B
C’
B’
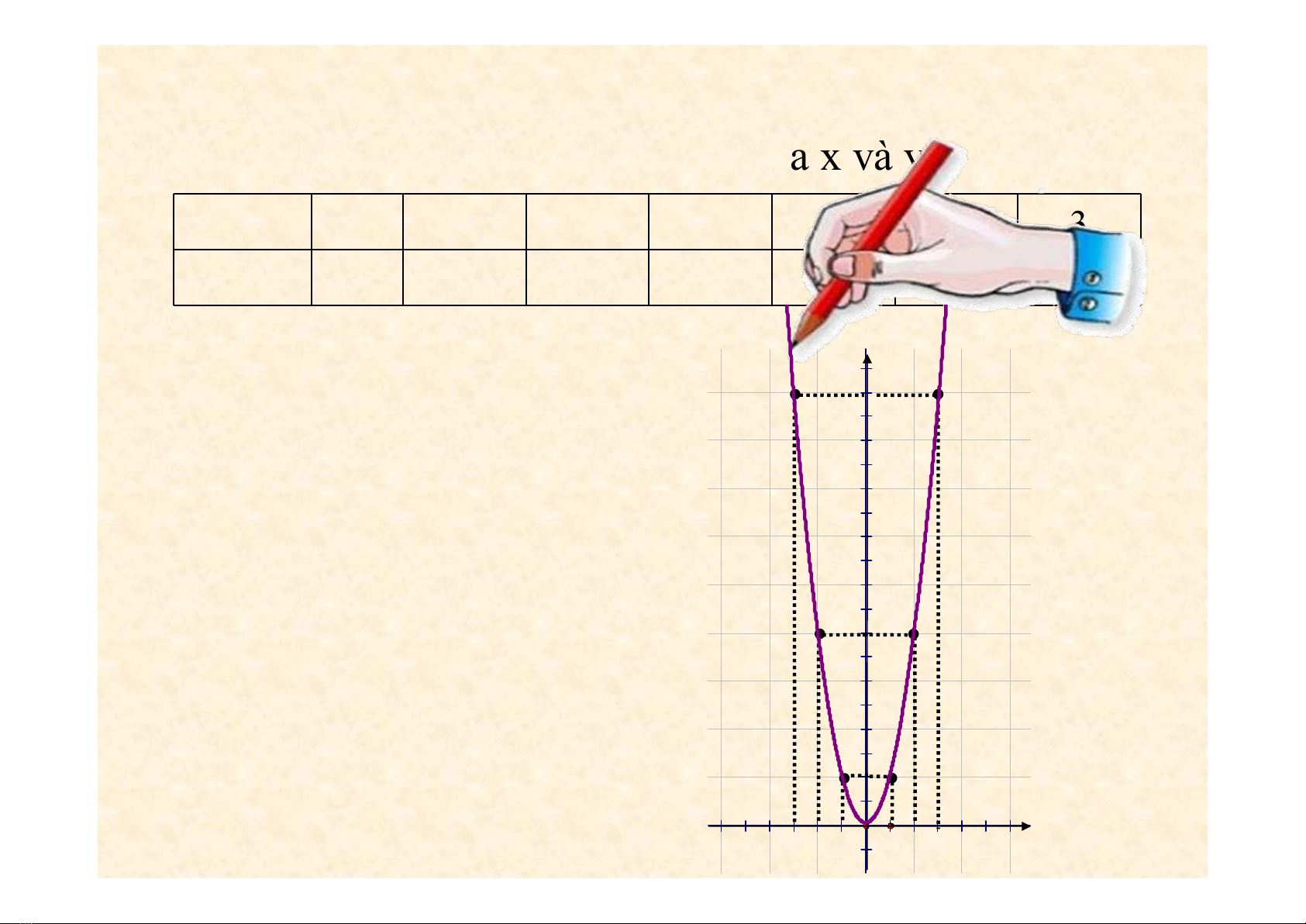
Ví dụ 1: Đồ thị hàm số y = 2x2
Bảng một số cặp giá trị tương ứng của x và y
x - 3 - 2 - 1 0 1 2 3
y = 2x218 8 2 0 2 8 18
y = 2x2
18
16
14
12
10
8
6
4
2
-15 -10 -5 5 10 15
0321- 1- 2-3
x
y
A
C
A’
B
C’
B’
Trên mặt phẳng toạ độ lấy các điểm:
A(- 3; 18), B (- 2; 8), C(- 1; 2),O(0; 0)
A’(3; 18), B’( 2; 8), C’( 1; 2)
Đồ thị hàm số y = 2x2 (a = 2 > 0)
- Là một đường cong đi qua
gốc toạ độ (Parabol đỉnh 0)
- Nằm ở phía trên trục hoành.
- Nhận 0y làm trục đối xứng.
-Điểm 0 là điểm thấp nhất.


























