
Ch−¬ng II
®éng lùc häc chÊt ®iÓm
Bμi gi¶ng VËt lý ®¹i c−¬ng
T¸c gi¶: PGS. TS §ç Ngäc UÊn
ViÖn VËt lý kü thuËt
Tr−êng §H B¸ch khoa Hμnéi

Isaac Newton

1. C¸c ®Þnh luËt Niut¬n
1.1 §Þnh luËt Niut¬n thø nhÊt:
ChÊt ®iÓm c« lËp constv =
r
1.2. §Þnh luËt Niut¬n thø hai:ChuyÓn ®éng cña
chÊt ®iÓm chÞu tæng hîp lùc F ≠0 lμchuyÓn
®éng cã gia tèc
Gia tèc cña chÊt ®iÓm ~ F vμ~ nghÞch víi m
v
r
0a0F ≠→≠
r
r
m
F
ka
r
r=Trong hÖ SI k=1 m
F
a
r
r=
Kh«ng chÞu mét t¸c dông nμo tõ bªn ngoμi,
chuyÓn ®éng cña nã ®−îc b¶o toμn
-> ®Þnh luËt qu¸n tÝnh
•Ph−¬ngtr×nhc¬b¶ncñac¬
häc chÊt ®iÓm: Fam
r
r
=
• HÖ qui chiÕu qu¸n tÝnh:
NghiÖm ®óng Ph−¬ng tr×nh Fam
r
r
=
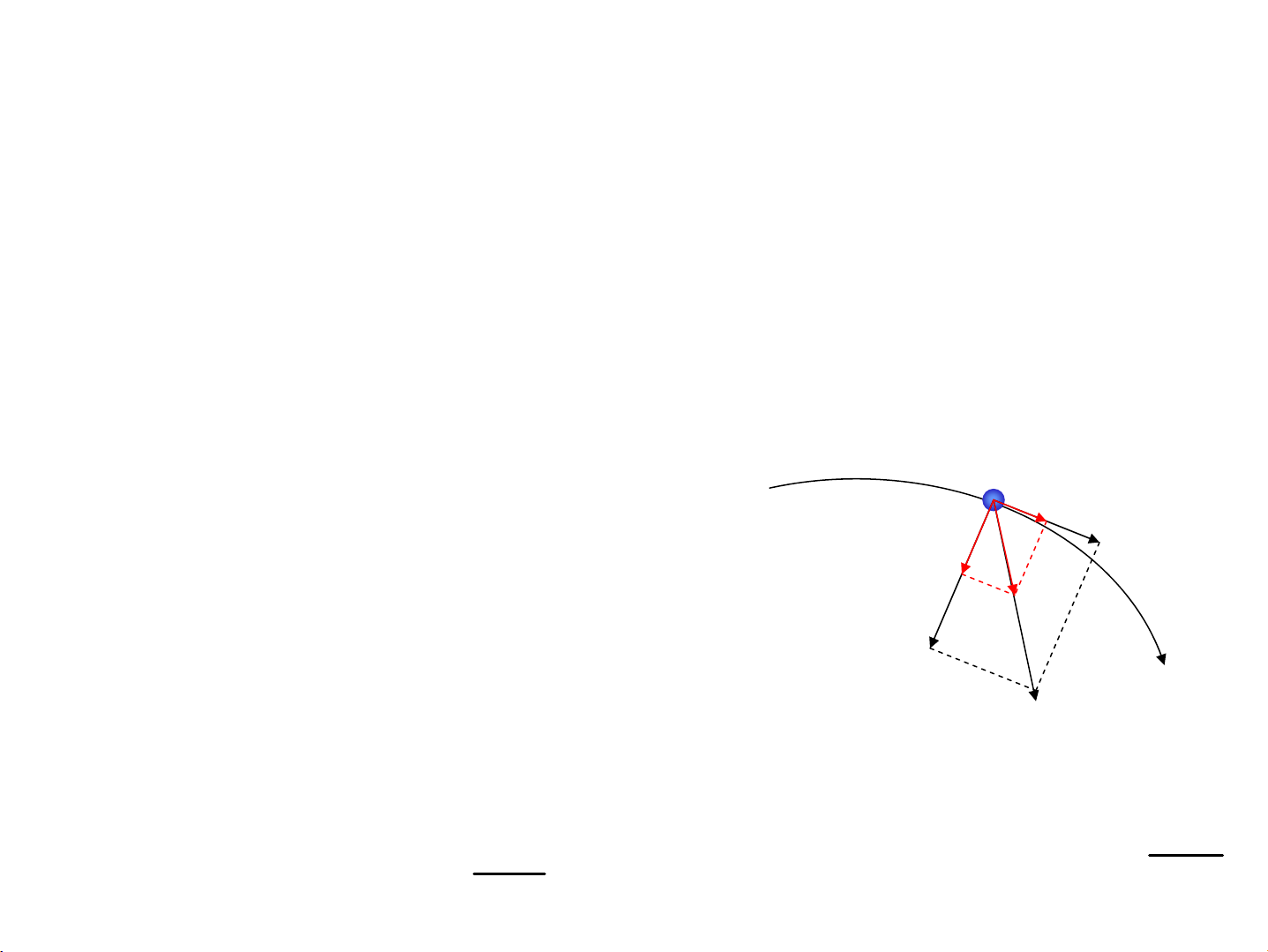
1.3.Lùc t¸c dông lªn chÊt ®iÓm trong
chuyÓn ®éng cong M
t
F
r
n
F
r
F
r
n
a
r
t
a
r
a
r
nt aaa
r
r
r
+
=
nt amamam
r
r
r
+
=
nt FFF
r
r
r+=
dt
dv
mFt=R
v
mF
2
n=
Lùc tiÕp
tuyÕn
Lùc ph¸p
tuyÕn
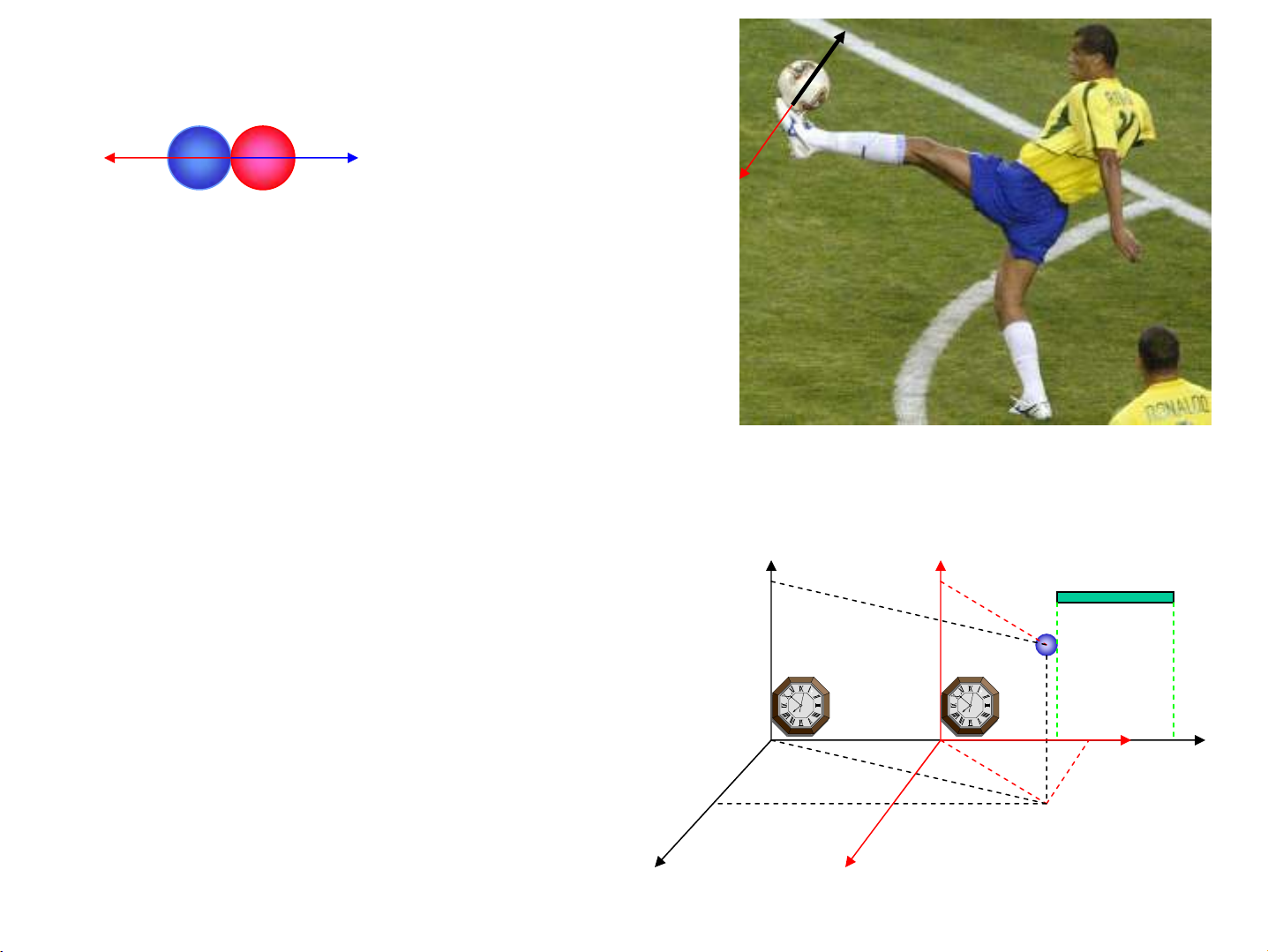
Tæng néi lùc trong hÖ =0
1.4. §Þnh luËt Niut¬n thø ba
'F
r
F
r
AB
'F
r
F
r
0'FF =+ r
r
2. ChuyÓn ®éng t−¬ng ®èi vμnguyªn lý Galilª
M
O’chuyÓn ®éng däc theo
ox víi vËn tèc , oy//o’y’,
oz//o’z’
Thêi gian lμtuyÖt ®èi:
t=t’ z
O
y
x
l=l’
x1x2
O’ x’
y’
z’
V
r
0'FF =+ r
r
2. ChuyÓn ®éng t−¬ng ®èi vμnguyªn lý Galilª



















![Đề thi học kì 1 Vật lý lớp 1 năm 2025-2026 (Đề số 2) [Có đáp án]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260210/hoahongcam0906/135x160/1981770793442.jpg)



![Đề thi học kỳ III Vật lý 1 năm 2024-2025 có đáp án [FULL]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260209/diegomaradona04/135x160/99561770719042.jpg)

![Bài tập Vật lý sóng: Tổng hợp bài tập 6 [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250805/oursky04/135x160/401768817575.jpg)
