
Giảng viên Vũ Đỗ Huy Cường
Chương 5
Chuỗi số
và
Chuỗi hàm
Giảng viên Vũ Đỗ Huy Cường Giải tích 1: Hàm số một biến 119 / 148

Giảng viên Vũ Đỗ Huy Cường
5.1. Dãy số và các phép tính
5.1.1. Khái niệm dãy số
Một dãy số vô hạn là một tập hợp có thứ tự của vô số số hạng.
Dãy số được mô tả bởi công thức tổng quát là một biểu thức chứa n
an=Q(n).(40)
Ví dụ
a) an=√n:{an}={1,√2,√3,√4,√5...}.
b) bn= (−1)n:{bn}={−1,1,−1,1,−1,1,−1,1,−1,1...}.
c) cn=n−1
n:{cn}={0,1
2,2
3,3
4,4
5...}
d) dn= (−1)n1
n:{dn}={−1,1
2,−1
3,1
4,−1
5...}.
Giảng viên Vũ Đỗ Huy Cường Giải tích 1: Hàm số một biến 120 / 148

Giảng viên Vũ Đỗ Huy Cường
5.1.2. Giới hạn của dãy số
Trong một số trường hợp, các số trong dãy sẽ tiến tới một giá trị nào
đó khi chỉ số ntang.
Ví dụ
a) cn=n−1
n:{cn}={0,1
2,2
3,3
4,4
5...} → 1.
b) dn= (−1)n1
n:{dn}={−1,1
2,−1
3,1
4,−1
5...} → 0.
Ngược lại, các số trong dãy có thể không tiến tới một giá trị nào đó khi
chỉ số ntang.
Ví dụ:
c) an=√n:{an}={1,√2,√3,√4,√5...} → ∞.
d) bn= (−1)n:{bn}={−1,1,−1,1,−1,1,−1,1,−1,1...} →?.
Giảng viên Vũ Đỗ Huy Cường Giải tích 1: Hàm số một biến 121 / 148
Giảng viên Vũ Đỗ Huy Cường
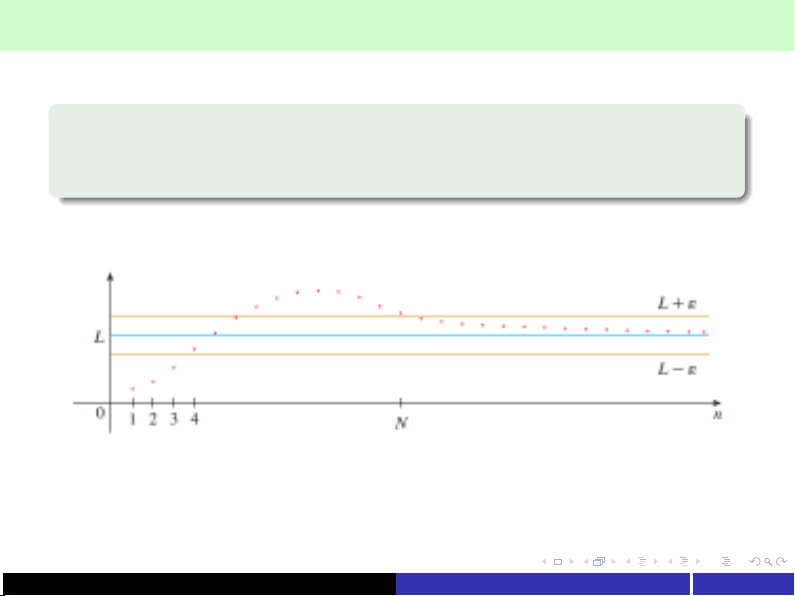
5.1.2. Giới hạn của dãy số
Dãy số {an}hội tụ đến số Lnếu với mọi số dương ǫtương ứng với
Nsao cho
∀n>N,|an−L|< ǫ.
Ta viết lim
n→∞
an=Lhoặc an→Lvà gọi Llà giới hạn của dãy số.
Nếu không có số Ltồn tại, ta nói rằng {an}phân kì.
Giảng viên Vũ Đỗ Huy Cường Giải tích 1: Hàm số một biến 122 / 148

Giảng viên Vũ Đỗ Huy Cường
5.1.2. Giới hạn của dãy số
Ví dụ:
a) lim
n→∞
1n=1. b) lim
n→∞
1
n=0.
c) lim
n→∞
an=∞với (a>1). d) lim
n→∞
an=0 với (0<a<1).
e) lim
n→∞
n
√n=1. f) lim
n→∞
n
√ln n=1.
g) lim
n→∞ 1+1
nn=e. h) lim
n→∞ 1−1
nn=e−1.
i) lim
n→∞
atnt+at−1nt−1+... +a0
bmnm+bm−1nm−1+... +b0=
∞t>m>0
at
bm
t=m,
0 0 <t<m
Giảng viên Vũ Đỗ Huy Cường Giải tích 1: Hàm số một biến 123 / 148


























