Nguy n Văn Quang – C đi n t 5ễ ơ ệ ử
Bài t p PTTĐ mô t trên Matlabậ ả
Bài 1: Xe l a.ử
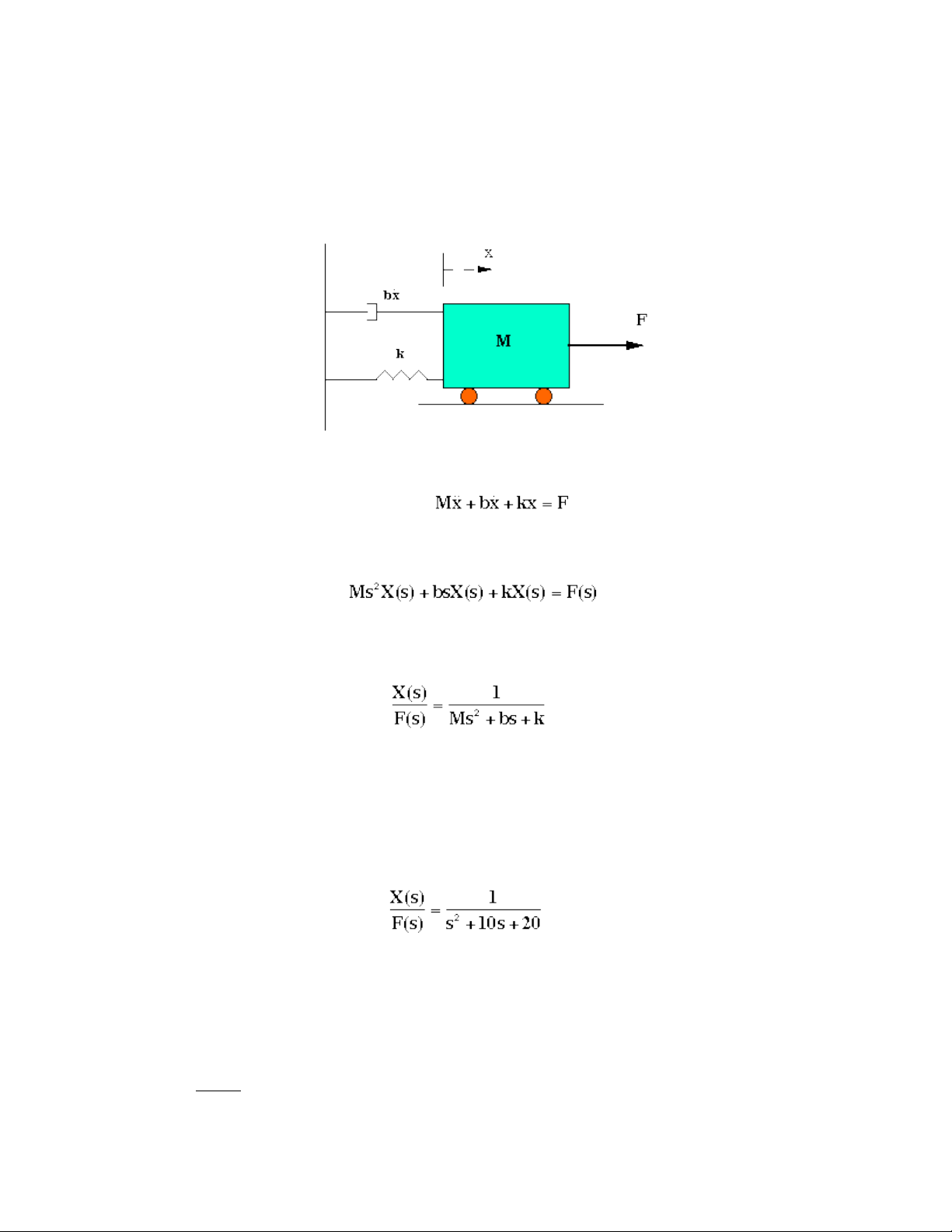
Đi u ki n ta có 1 h kh i l ng, lò xo và ch ng rung nh sau. ề ệ ệ ố ượ ố ư
Ph ng trình đ ng l c h c c a h th ng trên làươ ộ ự ọ ủ ệ ố
(1)
Bi n đ i Laplace t (1), ta có ế ổ ừ
Hàm truy n gi a d ch chuy n X(s) và đ u vào F(s) bây gi là ề ữ ị ể ầ ờ
L y các giá tr ấ ị
•M = 1kg
•b = 10 N.s/m
•k = 20 N/m
•F(s) = 1
L p các giá tr trên vào hàm truy n ta có ắ ị ề
Tr c h t ta kh o sát đáp ng b c thang đ n v c a h th ng h . T o m t m-file cóướ ế ả ứ ậ ơ ị ủ ệ ố ở ạ ộ
các l nh nh sau: ệ ư
num=1;
den=[1 10 20];
plant=tf(num,den);
step(plant)
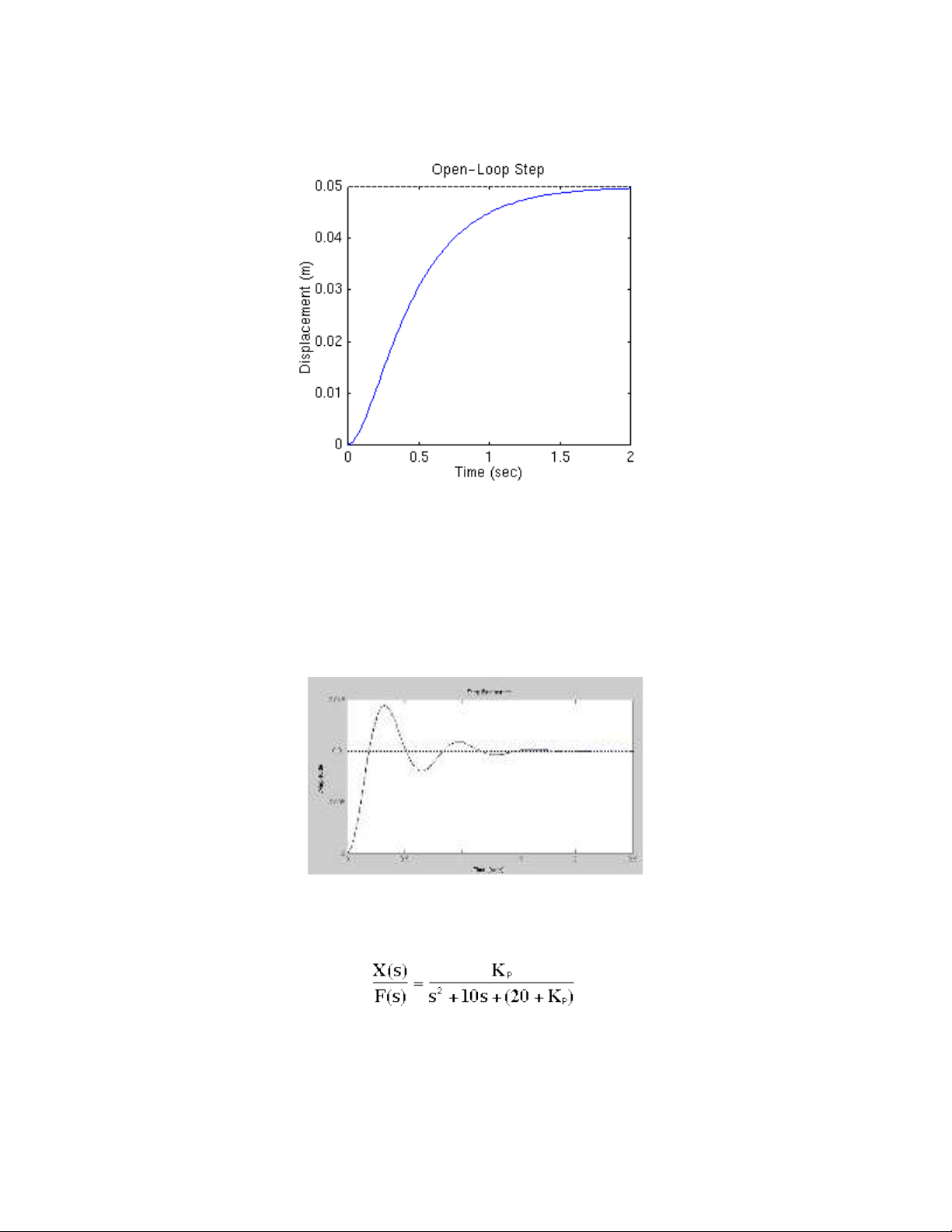
Ch y m-file này ta s có đ th nh sau. ạ ẽ ồ ị ư
Thay đ i các giá tr c a M, b, k ta cóổ ị ủ
num=1;
den=[1 5 100];
plant=tf(num,den);
step(plant)
Ch y m-file này ta s có đ th nh sau. H1ạ ẽ ồ ị ư
Lu t đi u khi n Pậ ề ể
. Hàm truy n đi u khi n vòng kín v i lu t đi u khi n P bây gi là: ề ề ể ớ ậ ề ể ờ
Ch n Kp = 300 và thêm vào m-file đo n mã l nh sau: ọ ạ ệ
Kp=300;
contr=Kp;
sys_cl=feedback(contr*plant,1);
t=0:0.01:2;
step(sys_cl,t)
Ch y m-file trong MATLAB ta đ c k t qu nh sau. ạ ượ ế ả ư
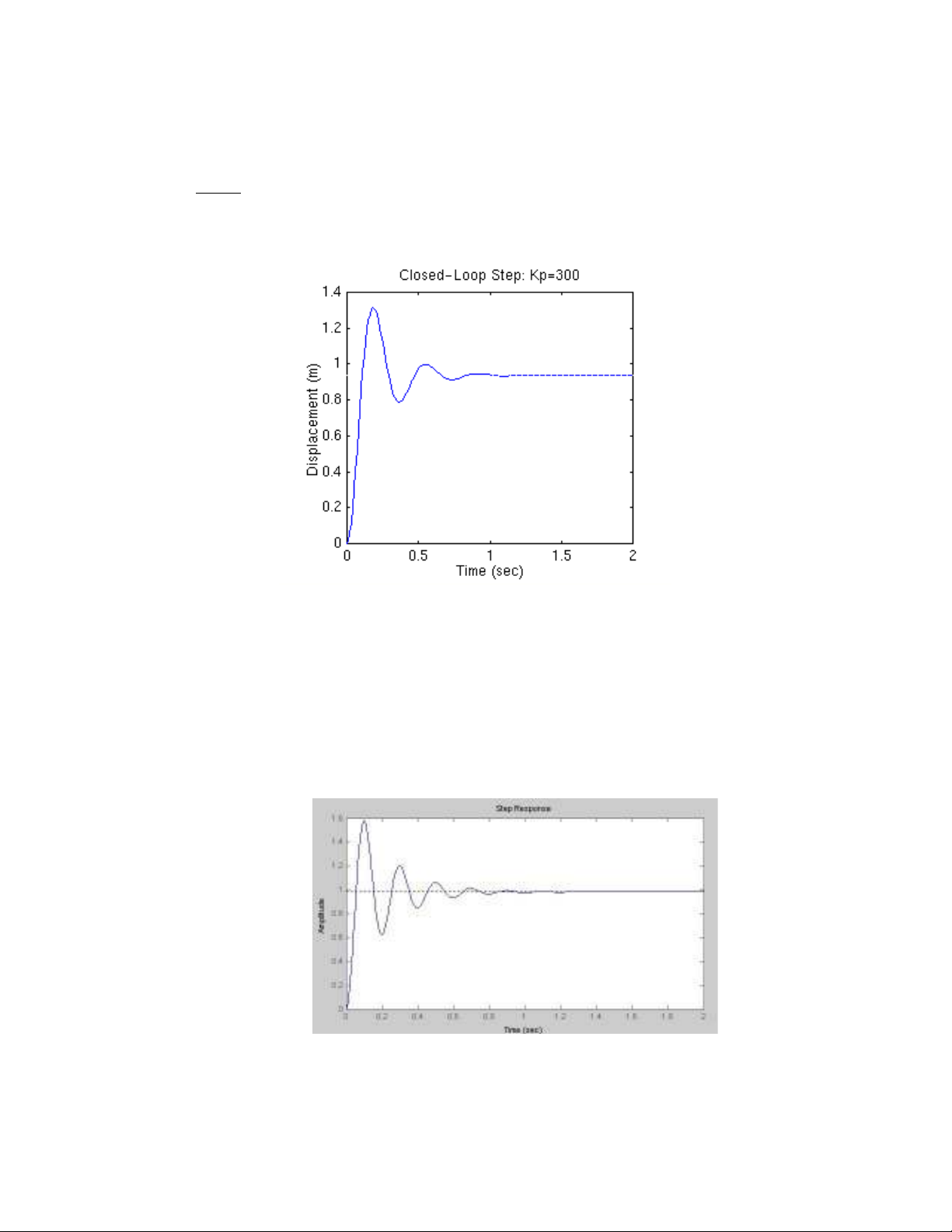
Thay đ i Kp= 1000 và thêm vào vào m-file đo n mã l nh nh sau: ổ ạ ệ ư
Kp=1000;
contr=Kp;
sys_cl=feedback(contr*plant,1);
t=0:0.01:2;
step(sys_cl,t)
Ch y m- file ta đ c k t qu nh sau: H2ạ ượ ế ả ư
Thay đ i Kp= 50 và thêm vào vào m-file đo n mã l nh nh sau: ổ ạ ệ ư
Kp=50;
contr=Kp;
sys_cl=feedback(contr*plant,1);
t=0:0.01:2;
step(sys_cl,t)
Ch y m- file ta đ c k t qu nh sau: H3 ạ ượ ế ả ư
Nh v y n u tăng P thì s làm gi m th i gian quá đ , tăng overshoot, và gi m steady-ư ậ ế ẽ ả ờ ộ ả
state error. Và ng c l iượ ạ
Đi u khi n t l -tích phânề ể ỉ ệ
Tr c khi xây d ng b đi u khi n PID, chúng ta xem xét t i lu t đi u khi n PI . Nhướ ự ộ ề ể ớ ậ ề ể ư
b ng t ng k t, ta th y r ng lu đi u khi n I làm gi m th i gian quá đ , nh ng làmả ổ ế ấ ằ ậ ề ể ả ờ ộ ư
tăng đ quá đi u ch nh và kéo dài th i gian đ n n đ nh c a h th ng, nh ng l i khộ ề ỉ ờ ế ổ ị ủ ệ ố ư ạ ử
đ c steady-state error. V i h th ng trên, chuy n thành hàm truy n vòng kín v i lu tượ ớ ệ ố ể ề ớ ậ
đi u khi n PI ta đ c hàm truy n m i: ề ể ượ ề ớ
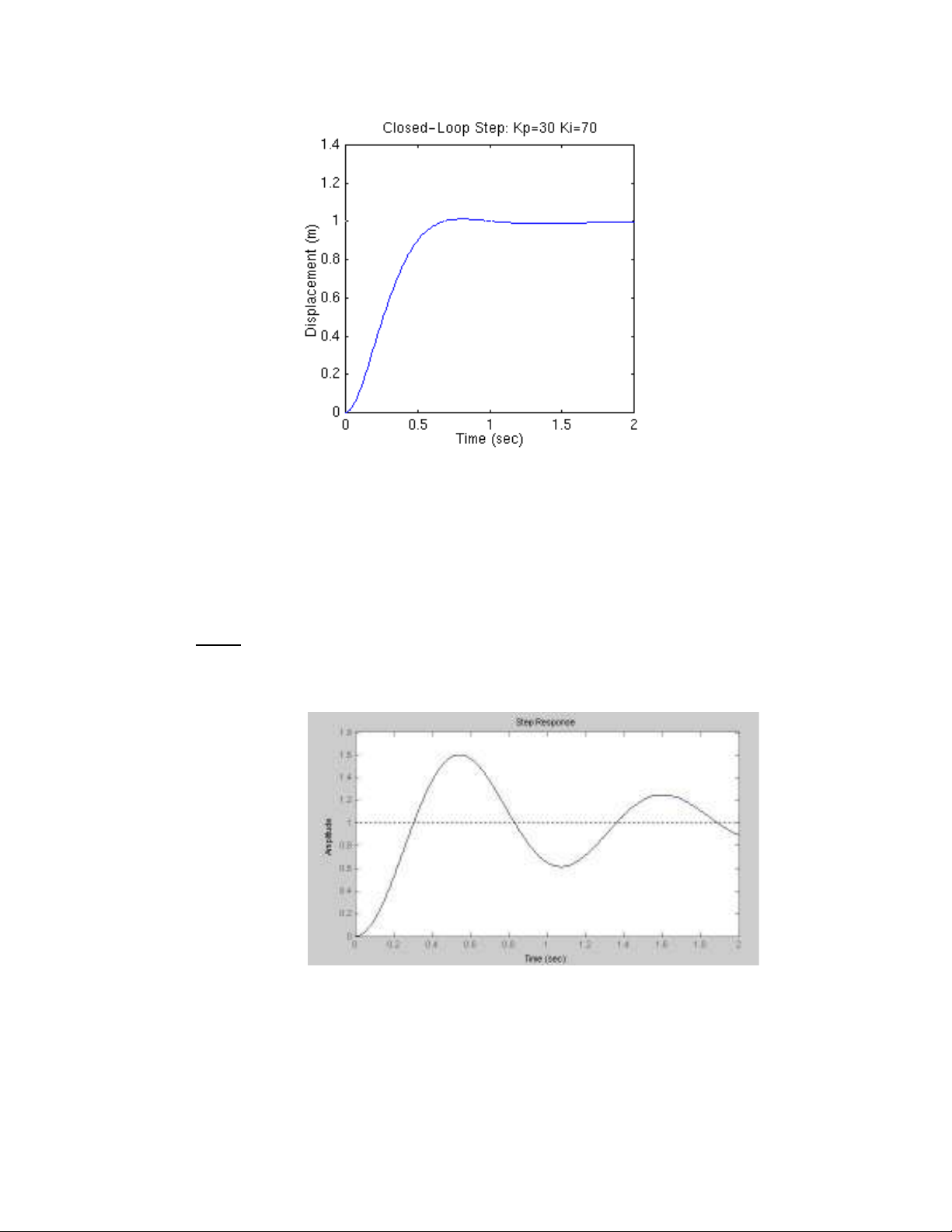
Bây gi ta ch n l i Kp = 30, Ki = 70. T o m-file v i các dòng l nh sau. ờ ọ ạ ạ ớ ệ
Kp=30;
Ki=70;
contr=tf([Kp Ki],[1 0]);
sys_cl=feedback(contr*plant,1);
t=0:0.01:2;
step(sys_cl,t)
Ch y ch ng trình trong MATLAB ta đ c đ th sau. ạ ươ ượ ồ ị
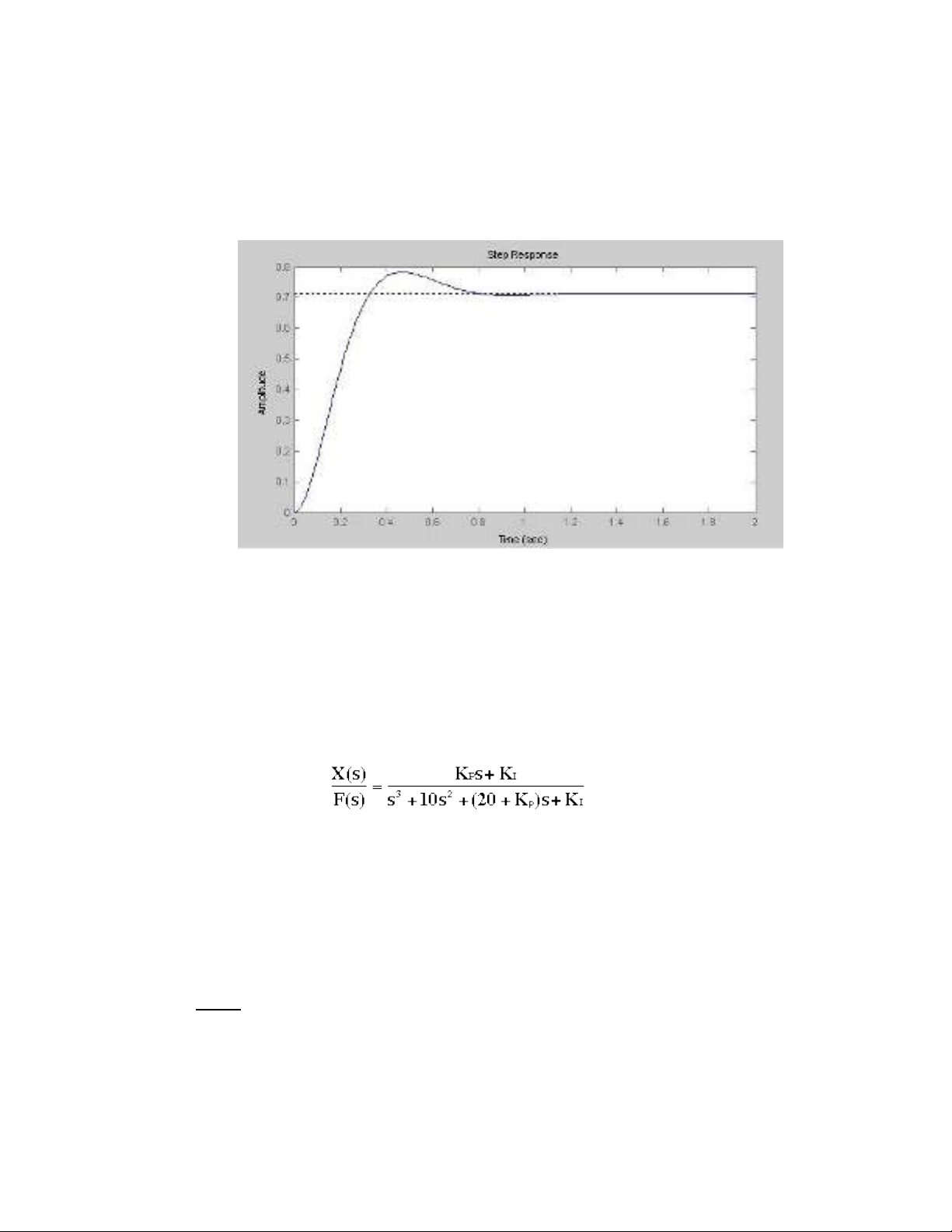
Gi nguyên giá tr Kp=30 và thay đ i Ki= 300 . T o dòng l nh trong m- file ta đ c ữ ị ổ ạ ệ ượ
Kp=30;
Ki=300;
contr=tf([Kp Ki],[1 0]);
sys_cl=feedback(contr*plant,1);
t=0:0.01:2;
step(sys_cl,t)
Ch y ch ng trình trong MATLAB ta đ c đ th sau. H4 ạ ươ ượ ồ ị
Nh vây là đúng nh quy lu t trong b ng đi u khi n I làm gi m th i gian quá đ ,ư ư ậ ả ề ể ả ờ ộ
nh ng làm tăng đ quá đi u ch nh và kéo dài th i gian đ n n đ nh c a h th ng,ư ộ ề ỉ ờ ế ổ ị ủ ệ ố
nh ng l i kh đ c steady-state error.ư ạ ử ượ
Đi u khi n t l -tích phân-vi phân(PID)ề ể ỉ ệ
Bây gi ta xét đ n b đi u khi n PID. Hàm truy n c a h th ng trên v i b đi uờ ế ộ ề ể ề ủ ệ ố ớ ộ ề
khi n PID vòng kín bây gi là: ể ờ