11
1
1
)( 2
2
2+
++
=
+
+=
+
+= LCp
RpLRLCp
LCp
pL
R
pC
pL
pC
pL
RpZv
0101010.
2
1
.10.10 2242 =++⇔ −−− pp
jppp 100010000101010.5 226 ±−=⇔=++⇔ −−
Nh v y d ng c a iư ậ ạ ủ Ctd s là : ẽ
))(1000cos(2 1000 AtAei t
Ctd
ψ
+= −
(1)
Theo (1) thì ta c n ph i xác đ nh 2 thành ph n c a iầ ả ị ầ ủ Ctd là A và
do đó ta c n ph iầ ả
tính hai s ki n , đây ta tính 2 s ki n ph thu c là iơ ệ ở ơ ệ ụ ộ C(0) và i’C(0).
b1.Tính các s ki n đ c l p iơ ệ ộ ậ L(0) và uC(0);
b11. Tính iL(0):
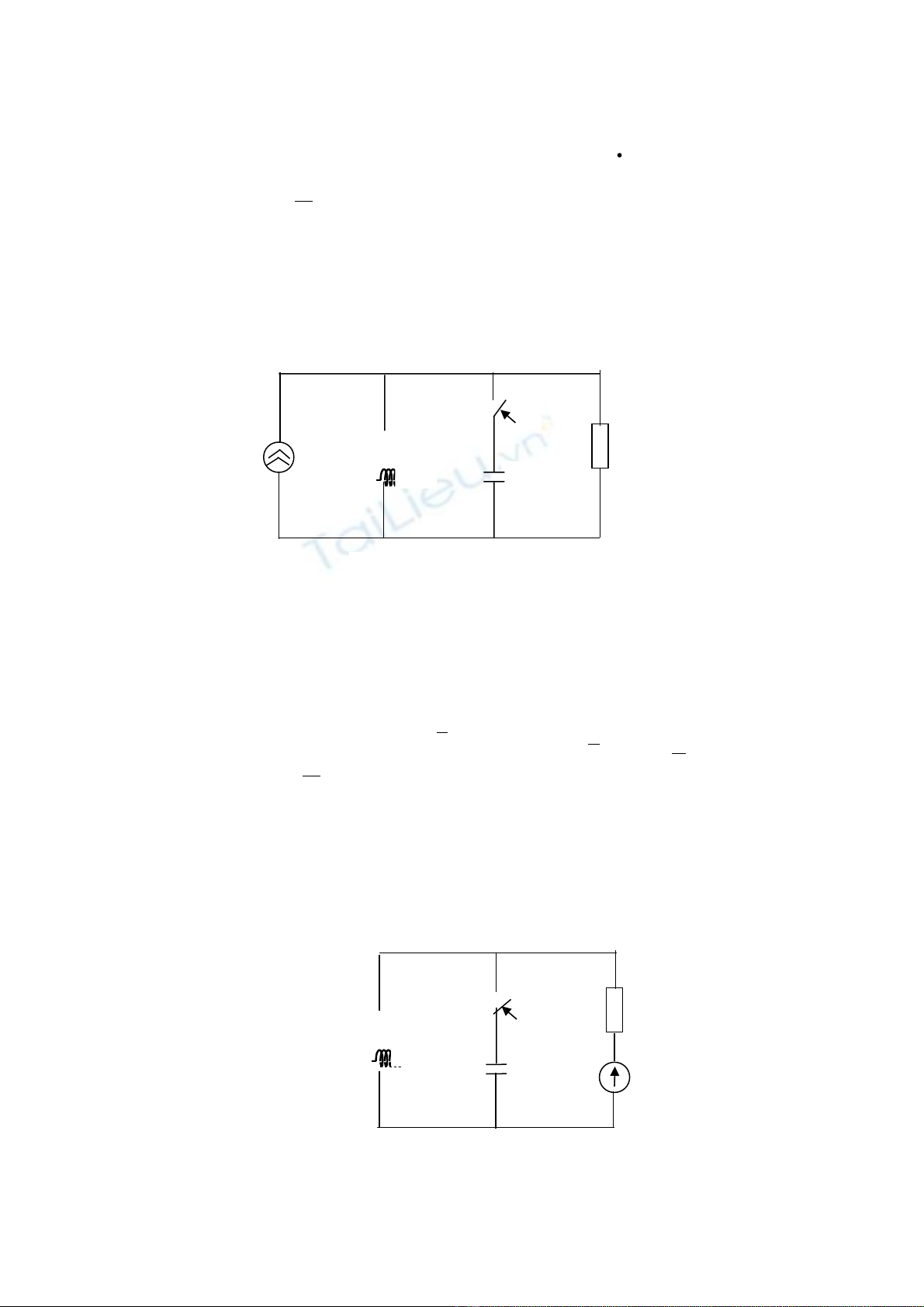
Xét m ch đi n tr c đóng K. Vì m ch ch đ xác l p nên ta dùng s ph cạ ệ ướ ạ ở ế ộ ậ ố ứ
đ tính iểL(t).Ta có :
)(1051,783,683,1
1010
30100 0
0
Aj
jjXR
E
I
L
L∠=+−=
+
−∠−
=
+
−
=
))(1051000sin(1,7)( 0AttiL+=⇒
(*)
Thay t=0 vào (*) ta đ c iượ L(-0)= 6,86 A
Vì bài toán ch nh nên ta có iỉL(-0) = iL(0) = 6,86 A
b12. Tính uC(0) :
Vì tr c đóng K uướ C ch a n p đi n và bài toán ch nh nên uư ạ ệ ỉ C(-0)=uC(0)=0
b2.Tính các s ki n iơ ệ C(0) và i’C(0) :
H ph ng trình theo t mô t m ch sau khi đóng Kệ ươ ả ạ
)3(
)2(
)1(
)()()(
0)()(
0)()()(
'
tetutRi
tutLi
tititi
CR
CL
RCL
−=−
=−
=−−
+−
=
=
−=
⇔
R
tute
ti
tutLi
tititi
c
R
CL
CLC
)()(
)(
)()(
)()()(
'
Thay t=0 vào h ph ng trình trên ta cóệ ươ :
==
=
=−=
⇔
+−
=
=
−=
⇔
Ai
i
Ai
R
ue
i
uLi
iii
R
L
C
c
R
CL
RLC
5
10
50
)0(
0)0(
8,158,6)0(
)0()0(
)0(
)0()0(
)0()0()0(
''
Đ o hàm hai v ph ng trình (1) và (3) ta đ cạ ế ươ ượ :
−=−
=−
=−−
)()(
1
)(
0)()(
0)()()(
''
'
'''
teti
C
tRi
tutLi
tititi
CR
CL
RCL
(**)
Thay t=0 vào (**) ta đ cượ :