Khoa Xaây Döïng & Cô Hoïc ÖÙng Duïng
Baøi taäp söùc beàn vaät lieäu trang 1 07/2013
Chöông 8
GIAÛI HEÄ SIEÂU TÓNH BAÈNG PHÖÔNG PHAÙP LÖÏC
I. TOÙM TAÉT LYÙ THUYEÁT
1. Caùc khaùi nieäm
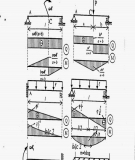
Heä cô baûn laø heä khoâng bieán hình ñöôïc suy ra töø heä sieâu tónh baèng caùch boû ñi caùc lieân keát
thöøa:
Baäc sieâu
tónh
Heä sieâu tónh Heä cô baûn Ñieàu kieän veà bieán
daïng
1
0
C
1
0
B
0
A
2
0, 0
B C
0, 0
A C
0, 0
A B
A
B
C
1
X
A
B
C
1
X
2
X
2
X
A
B
C
1
X
2
X
A
B
C
A
B
C
1
X
A
B
C
1
X
A
B
C
A
B
C
1
X
A
B
C
1
X
A
B
C

Khoa Xaây Döïng & Cô Hoïc ÖÙng Duïng
Baøi taäp söùc beàn vaät lieäu trang 2 07/2013
2. Heä phöông trình chính taéc
Ñeå heä cô baûn töông ñöông vôùi heä sieâu tónh thì chuyeån vò trong heä cô baûn i
taïi caùc vò trí vaø theo caùc phöông sieâu tónh ( phöông cuûa caùc aån soá i
X
) do caùc phaûn
löïc i
X
vaø do ngoaïi löïc gaây ra phaûi baèng khoâng. Vì chuyeån vò naøy phuï thuoäc vaøo
taûi troïng P vaø phuï thuoäc vaøo caùc aån soá
i
X
neân ta coù:
1 2
, ,..., , 0
i i n
X X X P
Ñoái vôùi heä ñaøn hoài tuyeán tính, coù theå aùp duïng nguyeân lyù coäng taùc duïng cuûa löïc:
1 1 2 2
... 0
i iP i i n in
X X X
Trong ñoù:
ik
- Chuyeån vò ñôn vò taïi vò trí vaø theo phöông löïc i
X
do löïc ñôn vò
1
k
X
gaây ra trong heä cô
baûn.
ip
- Chuyeån vò taïi vò trí vaø theo phöông löïc i
X
do taûi troïng gaây ra trong heä cô baûn.
Cho i = 1, 2,..., n ta ñöôïc heä phöông trình baäc nhaát ñoái vôùi n aån soá Xi nhö sau:
1 1 11 2 12 1
2 1 21 2 22 2
1 1 2 2
... 0
... 0
................
... 0
P n n
P n n
nP n n n nn
X X X
X X X
X X X
ii
laø heä soá chính:
iiiiiiii QQNNMM
ik
, vôùi
k
i
: laø heä soá phuï:
kikikikiik QQNNMM
ip
: laø soá haïng töï do taûi troïng:
000
PiPiPiiP QQNNMM
iii
Q
,
N
,
M
: laø bieåu ñoà moâ men uoán, löïc doïc, löïc caét do moâ men uoán, löïc doïc, löïc caét ñôn vò
1
X
i gaây ra trong heä cô baûn.
kkk
Q
,
N
,
M
: laø bieåu ñoà moâ men uoán, löïc doïc, löïc caét do moâ men uoán, löïc doïc, löïc caét ñôn vò
1
X
k gaây ra trong heä cô baûn.
000 ,, PPP QNM : laø bieåu ñoà moâ men uoán, löïc doïc, löïc caét do taûi troïng gaây ra trong heä cô baûn.
Giaûi heä phöông trình chính taéc ta tìm ñöôïc caùc aån soá i
X
.
II. VÍ DUÏ
VD.10.1. Thanh
AD
tuyeät ñoái cöùng chòu lieân keát khôùp xoay taïi
B
vaø ñöôïc giöõ bôûi hai thanh
AF
vaø
CE
. Caùc thanh
AF
vaø
CE
laøm cuøng vaät lieäu coù öùng suaát cho pheùp
2
19,5 /
kN cm
, moâ ñun
ñaøn hoài
4 2
2,1.10 /
E kN cm
. Heä chòu löïc
250
P kN
vaø coù kích thöôùc nhö hình V.10.1.
a) Xaùc ñònh öùng löïc trong caùc thanh
,
AF CE
.
b) Xaùc ñònh giaù trò öùng suaát phaùt sinh trong hai thanh
AF
vaø
CE
.
c) Tính chuyeån vò thaúng ñöùng cuûa ñieåm
D
.

Khoa Xaây Döïng & Cô Hoïc ÖÙng Duïng
Baøi taäp söùc beàn vaät lieäu trang 3 07/2013
Choïn heä cô baûn nhö hình veõ
Phöông trình chính taéc: 1 1 11
0 (*)
PX
Xeùt caân baèng thanh
AD
:
1 1
1
0 .40 .20 .40 0
2
B AF AF
m N X P N P X
Khi 1
0 , 0
AF CE
X N P N
Khi 1
1
0, 1 , 1
2
AF CE
P X N N
Ta coù: 1
1
.
.
20
240
.9 9
AF AF
P AF
AF AF
P
N N
P
L
E F E E
11
1 1
.
..
1.1 65
2 2 40 30
.9 .12 18
CE CE
AF AF
AF CE
AF AF CE CE
N NN N L L
E F E F E E E
Töø (*) ta coù:
1
1
11
1
8
13
1 1 8 9
2 2 13 13
P
CE
AF
N X P
N P X P P P
Öùng suaát phaùt sinh trong caùc thanh
AF
vaø
CE
:
P
40
cm
20
cm
20
cm
A
B
C
D
1
X
B
Y
AF
N
P
40
cm
20
cm
20
cm
A
B
C
D
F
4 2
2
40
2.10 /
9
L cm
E kN cm
F cm
1
X
P
40
cm
20
cm
20
cm
2
30
12
L cm
F cm
A
B
C
D
E
F
2
40
9
L cm
F cm
Hình V.10.1

Khoa Xaây Döïng & Cô Hoïc ÖÙng Duïng
Baøi taäp söùc beàn vaät lieäu trang 4 07/2013
2
2
8250
13 12,82 /
12
9250
13 19, 23 /
9
CE CE
z
CE
AF AF
z
AF
NkN cm
F
N
kN cm
F
Chuyeån vò thaúng ñöùng cuûa ñieåm
D
:
14
9.250. 1
.13
40 0,038
2.10 .9
AF AF
P AF
AF AF
N N
L cm
E F
VD.10.2. Thanh
ABCD
tuyeät ñoái cöùng chòu lieân keát khôùp xoay taïi
A
vaø ñöôïc giöõ bôûi thanh
,
BF DE
nhö hình V.10.2a. Hai thanh
BF
vaø
DE
laøm baèng theùp coù moâ ñun ñaøn hoài
4 2
2,1.10 /
E kN cm
vaø öùng suaát cho pheùp
2
18,5 /
kN cm
vaø coù dieän tích maët caét ngang laàn löôït
laø
F
vaø
2
F
. Cho:
250 / ; 2,5
q kN m a m
.
a) Xaùc ñònh öùng löïc trong caùc thanh
BF
vaø
DE
theo
,
q a
.
b) Xaùc ñònh dieän tích maët caét ngang,
F
, ñeå caùc thanh
BF
vaø
DE
cuøng beàn.
c) Vôùi
F
tìm ñöôïc, tính chuyeån vò thaúng ñöùng taïi
D
.
Choïn heä cô baûn nhö hình V.10.2b
Phöông trình chính taéc: 1 1 11
0 (*)
PX
Xeùt caân baèng thanh
ABCD
:
0
1 1
2
0 .2 . sin 45 .2 . .2,5 .3 0 1,5
3
A DE DE
m q a a X a q a a N a N qa X
2
a
2
a
a
A
B
C
D
q
q
1
X
A
Y
A
X
DE
N
0
45
2
a
Hình
V.10.2
2
a
a
A
B
C
D
E
F
EF
, 2
E F
q
q
2
a
2
a
a
A
B
C
D
E
F
, 2
E F
q
q
1
X
)
a
)
b

Khoa Xaây Döïng & Cô Hoïc ÖÙng Duïng
Baøi taäp söùc beàn vaät lieäu trang 5 07/2013
Khi 1
0 1,5 , 0
DE BF
X N qa N
Khi 1
2
0, 1 , 1
3
DE BF
q X N N
Ta coù:
2 2
1
2
1,5 . 3
.2 0,707
22
DE DE
P DE
DE DE
qa
N N
qa qa
L a
E F E F EF
EF
11
2 2
.
3 3
. . 1.1 2
2 2 2 2 2 3,05
2 9
DE DE BF BF
DE BF
DE DE BF BF
N N N N
a a
L L a a
E F E F E F EF EF EF
Töø (*) ta coù:
1
1
11
1
0,232
2 2
1,5 1,5 0,232 1,39
3 3
P
BF
DE
N X qa
N qa X qa qa qa
Ta coù:
0, 232 1,39
2
BF DE
z z
qa qa
F F
Theo ñieàu kieän beàn:
2
max
1,39 1,39 1,39.250.2,5 23,48
2 2 2.18,5
z
qa qa
F cm
F
Choïn
2
23,5
F cm
Chuyeån vò thaúng ñöùng taïi
D
: 2 2 3
4
.1,39 .2 1,39 1,39.250.2,5 .10 4,62
2 2.10 .23,5
DE DE
DE
DE DE
N L qa a qa
L mm
E F E F EF
VD.10.3. Thanh gaõy khuùc ABC tuyeät ñoái cöùng chòu lieân keát goái coá ñònh taïi
B
vaø ñöôïc giaèng bôûi
caùc thanh
CE
vaø
CD
nhö hình V.10.3a. Caùc thanh
CE
vaø
CD
coù cuøng dieän tích maët caét ngang
F
,
moâñun ñaøn hoài 24 /10.2 cmKNE vaø öùng suaát cho pheùp
2
19 /
kN cm
. Cho: 200
P KN
.
a) Xaùc ñònh öùng löïc trong caùc thanh
CE
vaø
CD
.
b) Xaùc ñònh dieän tích
F
caùc thanh
CE
vaø
CD
beàn.
c) Tính chuyeån vò thaúng ñöùng taïi
A
.
Choïn heä cô baûn nhö hình V.10.3b
Phöông trình chính taéc: 1 1 11
0 (*)
PX
Xeùt caân baèng thanh ABC nhö hình V.10.3c:
m2m2m1
P
0
60
A
B
C
D
E
Hình
V.10
.3
)
a
)
b
0
45
m2
3
m
P
0
60
A
B
C
E
0
45
1
X
m2
P
0
60
A
B
C
1
X
0
45
CE
N
B
Y
)
c
m2
B
X