Baøi taäp Tröôøng ñieän töø
Ngöôøi soaïn: Leâ Minh Cöôøng
[lmcuong@hcmut.edu.vn]
Chöông 1: Caùc khaùi nieäm
vaø luaät cô baûn.
Chöông 2: Tröôøng ñieän tónh.
Chöông 3: Tröôøng ñieän töø döøng.
Chöông 4: Tröôøng ñieän töø
bieán thieân.
Chöông 5: Böùc xaï ñieän töø.
Chöông 6: OÁng daãn soùng
- Hoäp coäng höôûng.
(Naêm hoïc 2007 – 2008)
Problem_ch1 2
TAØI LIEÄU THAM KHAÛO
1. Tröôøng ñieän töø , Ngoâ Nhaät AÛnh – Tröông Troïng Tuaán Myõ , NXB ÑHQG TP
HCM , 2000 .
2. Baøi Taäp Tröôøng ñieän töø , Ngoâ Nhaät AÛnh – Tröông Troïng Tuaán Myõ , NXB
ÑHQG TP HCM , 2000 .
3. Elements of Engineering Electromagnetics (second edition) , Nannapaneni
Narayana Rao , Prentice-Hall , 1987.
4. Electromagnetic : concepts & applications (second edition) , Stanley V.Marshall
& Gabriel G.Skitek , Prentice-Hall , 1987.
5. Electromagnetics (fourth edition) , John D.Kraus , McGraw-Hill , 1991.
6. Schaum’s Outline of Theory and Problems of Electromagnetics (second edition) ,
Joseph A.Edminister , McGraw-Hill , 1993.
7. Engineering Electromagnetics (seventh edition) , William H. Hayt, Jr. and John
A. Buck , McGraw-Hill , 2006.
Problem_ch1 3
BAØI TẬP CHƯƠNG 1
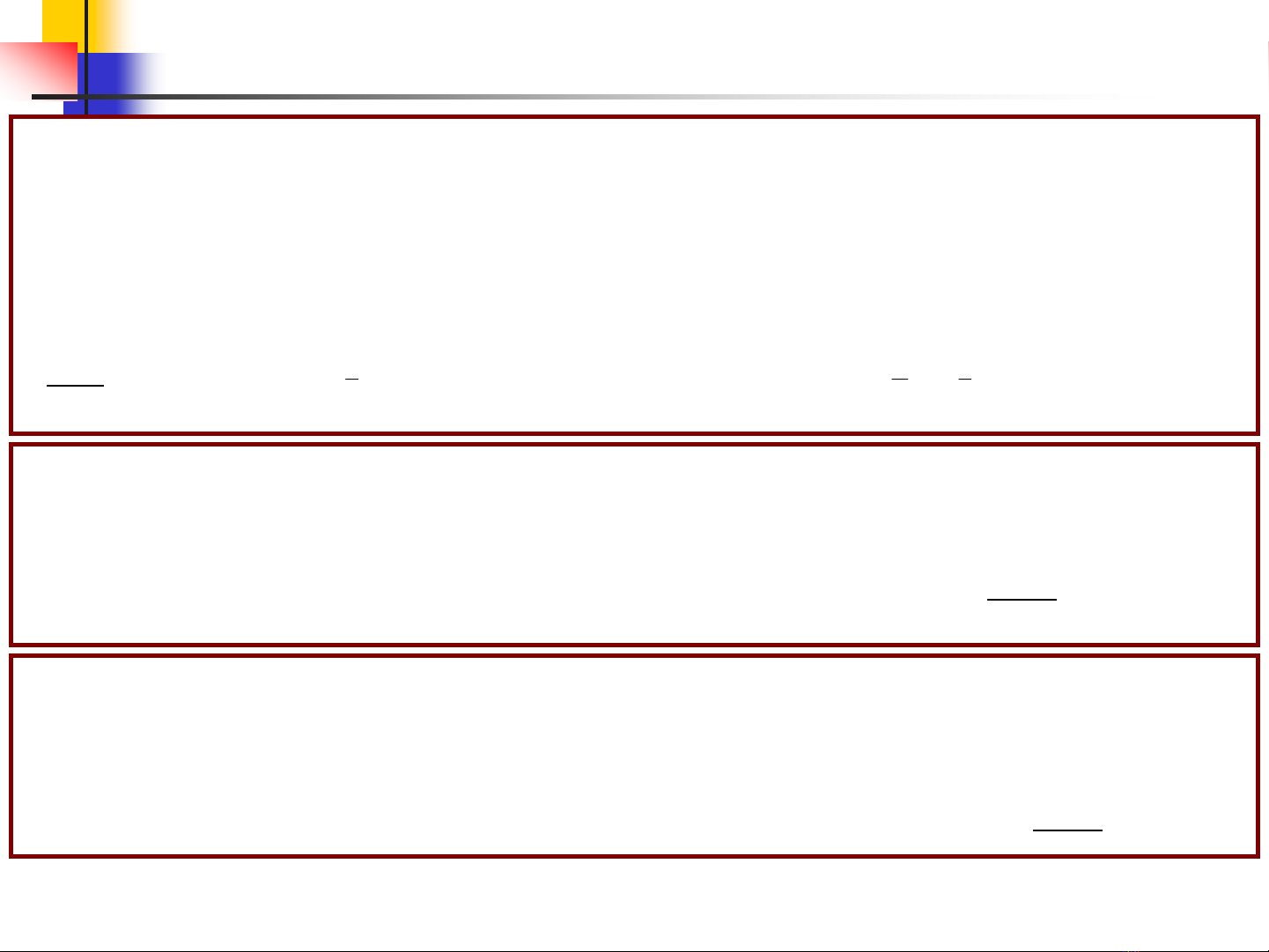
(ÑS: )
11
343
2i 3i 2i ; i 2i 2i ;3; 2i 2i i ; ; 2i 2i i
xyz xyz xyz xyz
π
→→ → →→ → →→→ →→→

+− +− −++ ±−++


A i i ; B i 2i 2i
x
yxyz
→→ → →→ → →
==++−
Cho 2 vectô :
Tìm : AB;i;A.B;AB; :
B
β
→→→ →→→→
+×
goùc nhoïn hôïp bôûi 2 vectô A& B
→→
n
→: vectô phaùp tuyeán cuûa maët phaúng chöùa A& B
→→
1.1:
(ÑS: 4.10-2 (C) )
Tìm ñieän tích chöùa trong quaû caàu, baùn kính 1/π(cm), coù maät ñoä ñieän tích phaân
boá khoái ρ= 1/r2(C/m3) ?
1.2 :
Ñóa troøn , bkính a, naèm trong maët phaúng Oxy, taâm taïi goác toïa ñoä , mang ñieän vôùi
maät ñoä maët : σ= 4πε0/r [C/m2]. Tìm ñieän tích Q cuûa ñóa ?
1.3 :
(ÑS: 8π2ε0a )
Problem_ch1 4
BAØI TẬP CHƯƠNG 1
Cho haøm voâ höôùng U = xy , tìm vectô ñôn vò vuoâng goùc vôùi maët U = xy = 2 taïi
ñieåm P(2,1,0) baèng 2 caùch :
+ Duøng tích coù höôùng cuûa 2 vectô tieáp tuyeán vôùi maët taïi P ?
+ Duøng khaùi nieäm gradient ?
Tìm toác ñoä bieán ñoåi cöïc ñaïi cuûa haøm U taïi P ?
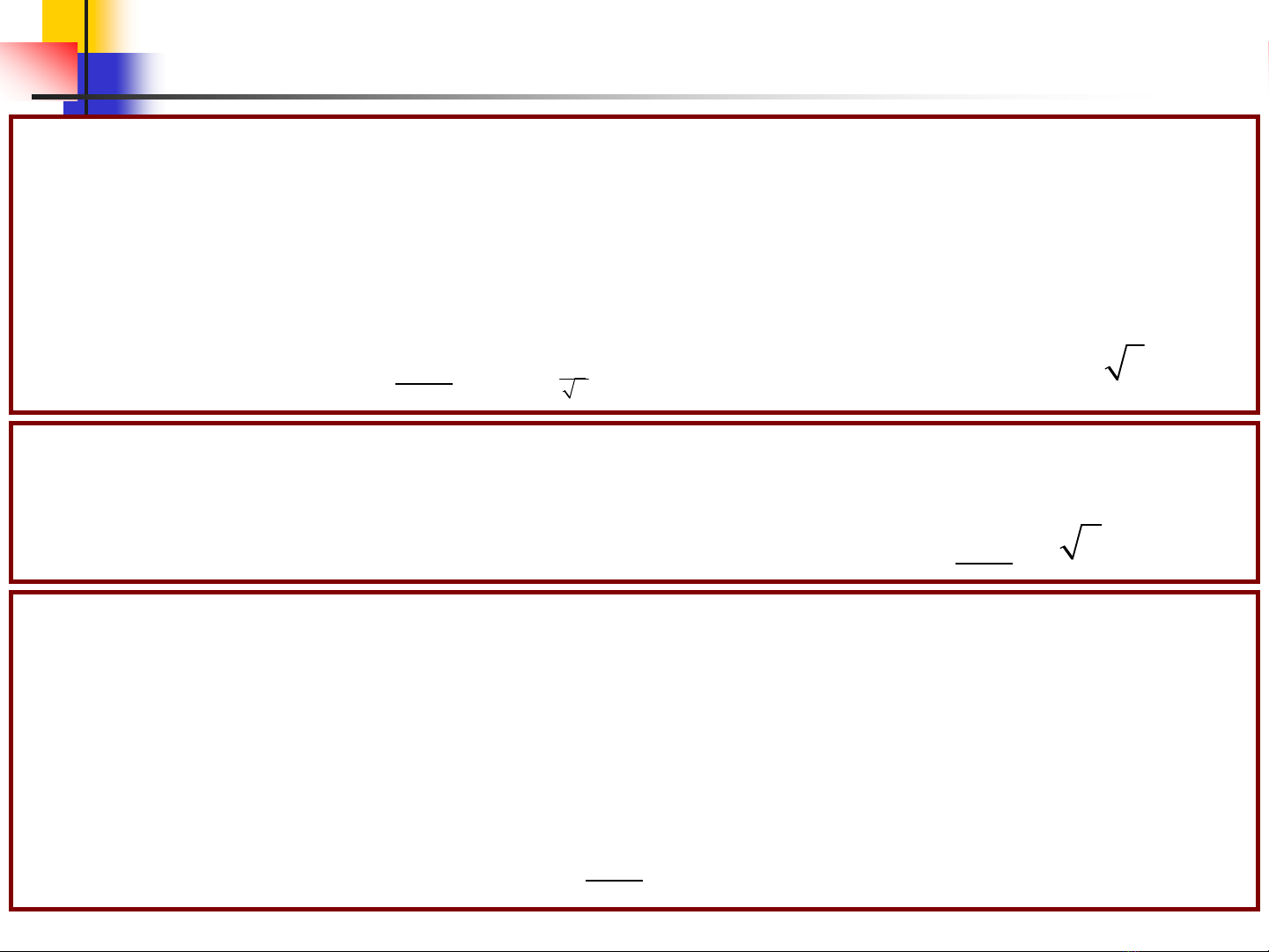
1.4 :
(ÑS: .Toác ñoä bieán ñoåi max = )
1
5
ii2i
nxy
→→→

=± +

 5
Cho haøm voâ höôùng U = r2sin(2φ) trong heä truï , tìm toác ñoä taêng cuûa haøm naøy
theo höôùng cuûa vectô taïi ñieåm P(2, π/4, 0) ?
1.5 :
Aii
r
φ
→→→

=+

 (ÑS: )
22
)0; )cos ; )4 2cosab cr
φ
θ
+
(ÑS: )
Tìm div cuûa caùc tröôøng vectô:
1.6 : 22
)A ( )i 2 i 4i
xyz
axyxy
→→→→

=− − +


)A cos i sin i
r
br r
φ
φφ
→→→

=−


2
)A i sin i
r
crr
θ
θ
→→ →

=+


(Heä truï)
(Heä caàu)
Problem_ch1 5
BAØI TẬP CHƯƠNG 1
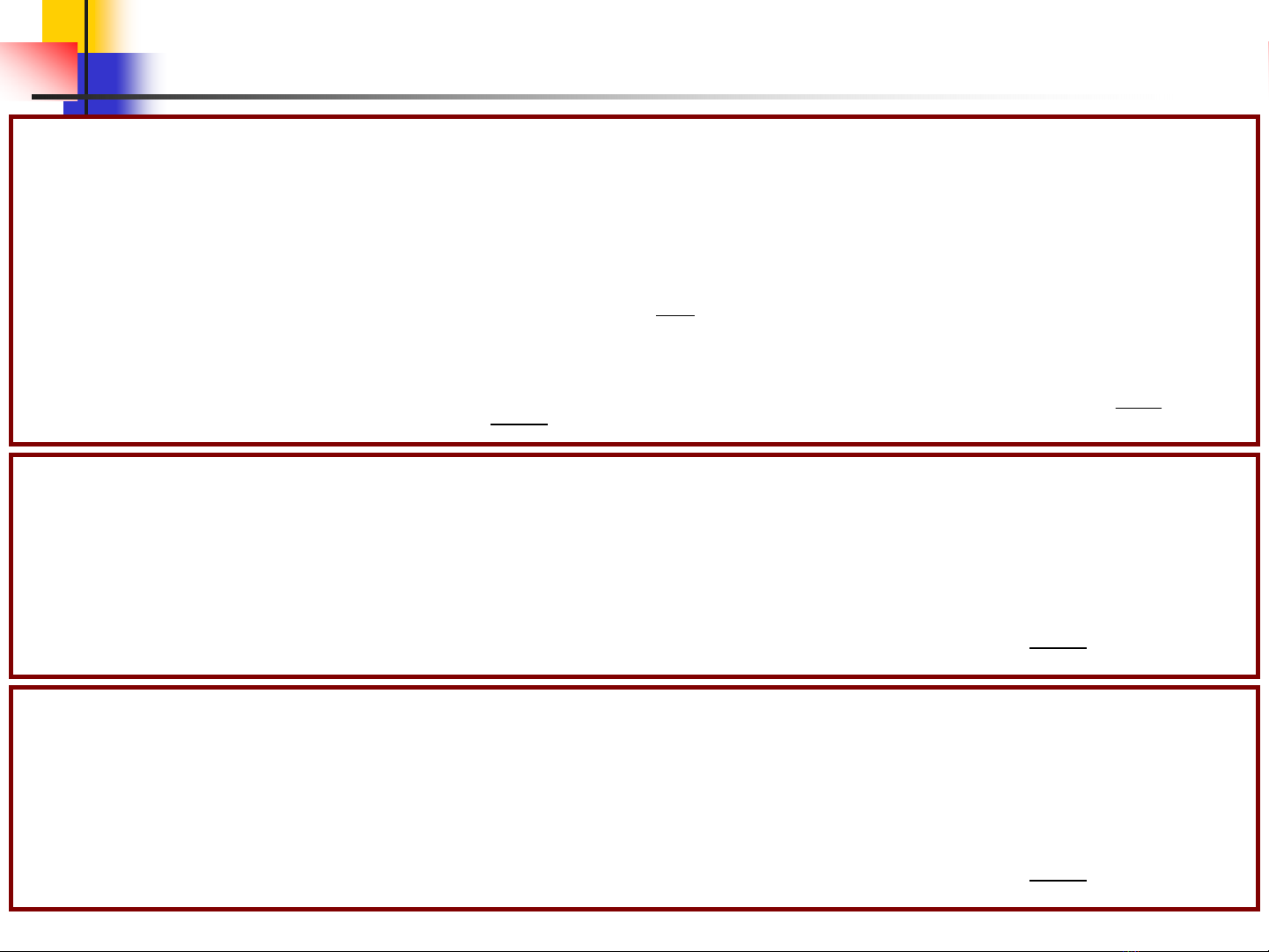
)2i;)2(1sin)i;) i
r
e
zz
r
ab c
φ
φ
→→→
−
−+ −
(ÑS: )
Duøng ñònh lyù Stokes, tìm löu soá cuûa vectô :
treân chu vi tam giaùc ABC theo chieàu ABC vôùi : A(0,0,0) ; B(0,1,0); C(0,0,1) ?
1.8 : F ( )i ( )i ( )i
x
yz
xy xz yz
→→→→

=+ +− ++


(ÑS: 1 )
Duøng ñònh lyù Divergence, tìm thoâng löôïng cuûa vectô vò trí gôûi qua moät maët truï
kín ñaùy troøn baùn kính a, taâm taïi goác toïa ñoä, cao h, truïc hình truï truøng truïc z ?
1.9 :
(ÑS: 3πa2h)
Tìm rot cuûa caùc tröôøng vectô:
1.7 : )A i i
xy
ayx
→→→

=−


)A 2 cos i i
r
br r
φ
φ
→→→

=+


)A i
r
e
r
c
θ
→→
−

=

(Heä truï)
(Heä caàu)