. Bài toán Steiner
1. Lịch sử bài toán Steiner
Vấn đề sau đây được Fermat, nhà toán học Pháp nổi tiếng, đề ra trong
cuốn sách “Treatise on Minima and Maximal” [2, trang 1], cụ thể là như
sau: “Cho trước ba điểm trong mặt phẳng. Hãy tìm điểm thứ tư sao cho
tổng khoảng cách từ điểm này tới ba điểm cho trước nhỏ nhất có thể. “
Bài toán của Fermat được Torricelli, học trò cuối cùng của Galileo, giải
vào quãng năm 1640 [2, trang 2]. Điểm này được mang tên là điểm
Torricelli của tam giác tạo bởi ba điểm đã cho. Đó là điểm nhìn ba cạnh
của tam giác tạo bởi 3 điểm đã cho dưới cùng một góc 120° nếu như tam
giác tạo thành có ba góc nhỏ hơn 120°, và là đỉnh góc tù nếu như tam
giác đó có một góc không nhỏ hơn 120°.
Sau nhiều thế kỷ, bài toán của Fermat lại được phát hiện lại trong một
khía cạnh mới bởi nhiều nhà toán học khác. Người ta tổng quát bài toán
Fermat như sau:
Bài toán Fermat: Cho trước một tập hợp hữu hạn n điểm trong mặt
phẳng. Hãy tìm một điểm sao cho tổng khoảng cách từ điểm này tới
các điểm cho trước nhỏ nhất có thể.
Điểm cần tìm được gọi là điểm Torricelli cho hệ n điểm cho trước.
Boltyanski, Scriba, Schreiber und Wesolowsky [2, trang 2] đã viết về lịch
sử của bài toán Fermat. Vào thế kỷ thứ 19, Steiner đã tổng quát bài toán
1
của Fermat bằng cách không hạn chế số điểm cần tìm. Quãng 100 năm
sau, Courant và Robin đã ghi chú về bài toán tổng quát này như sau:
“Một vấn đề rất giản đơn nhưng lại rất có tính kiến thiết là vấn đề
được nêu ra bởi Jacob Steiner, một đại diện nổi tiếng của trường
phái hình học Berlin, vào đầu thế kỷ 19. Ba làng A, B và C phải
được nối với nhau bởi một hệ thống đường giao thông với tổng
độ dài nhỏ nhất có thể.”
Hình 31
Thực ra, ngay từ thời Gauß, người ta đã biết tới những loại bài toán kiểu
như thế này. Trong một bức thư gửi cho một người bạn của mình tên là
Schumacher, Gauß có viết:
2
“Nếu đề cập tới vấn đề thiết kế một mạng giao thông tối ưu cho
các đỉnh một tứ giác, thì ta gặp phải một bài toán thật sự thú vị,
mà tôi đã biết tới nó khi phải thiết kế các tuyến đường sắt nối các
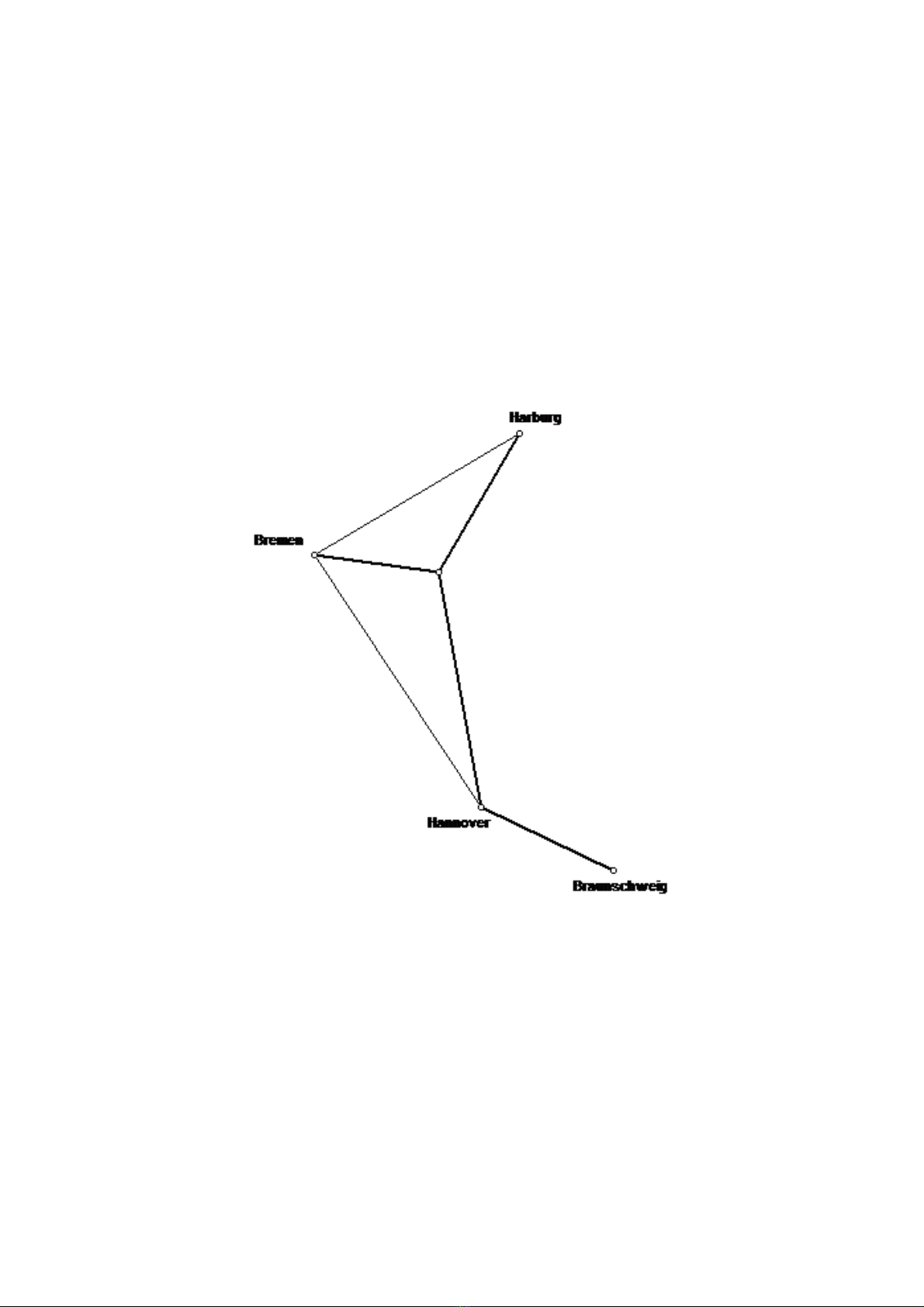
thành phố Harburg, Bremen, Hannover và Braunschweig... “
Trong cuốn sách “What is Mathematics” của Robbins và Courant xuất
bản năm 1941, bài toán của Gauß được công bố dưới tên của Steiner:
Bài toán Steiner: Cho trước một tập hợp hữu hạn n điểm trên mặt phẳng
(hoặc trong không gian metric nào đó), hãy tìm mạng giao thông với
tổng độ dài nhỏ nhất nối các điểm này với nhau.
Bài toán của Steiner cho tập hợp gồm 3 điểm cho trước chính là một
trường hợp riêng của bài toán Fermat. Thế nhưng, với tập hợp có 4 điểm,
ta thấy rằng bài toán Steiner không còn là bài toán của Fermat nữa, và nó
hoàn toàn có một màu sắc khác.
Tuy vậy, chính Robbins và Courant cũng không hề đề cập tới bài toán
Fermat trong trường hợp riêng của bài toán Steiner cho n = 3, cũng như
không đề cập gì tới bài toán của Gauß khi n = 4. Cũng do sự hấp dẫn và
sự phổ cập của cuốn sách của họ, mà bài toán được đặt ra thật sự trở
thành “vấn đề Steiner” và mối quan tâm tới bài toán này được thổi bùng
lên.
Bài toán mà Gauß đặt ra cho hệ thống các đường tàu nối các thành phố
Harburg, Bremen, Hannover và Braunschweig được Bopp giải quyết một
3
cách triệt để [2]. Trong hình 31, chúng ta đã thấy mô tả lời giải của bài
toán này. Hệ thống đường sắt tối ưu được bổ sung thêm một điểm, điểm
Torricelli của tam giác với ba đỉnh là ba thành phố Harburg, Bremen,
Hannover, và Braunschweig được nối với Hannover bởi một tuyến đường
sắt chạy thẳng.
Melzak [2], vào năm 1961, đã là người đầu tiên nêu lên những tính chất
cơ sở để xác định mạng giao thông tối ưu cho bài toán Steiner n điểm bất
kỳ. Một tổng quan về bài toán Steiner trên mặt phẳng Ơcơlit được đưa ra
bởi Gilbert và Pollak trong năm 1968.
Vì lý do tối ưu, cho nên chúng ta nhận thấy ngay là mạng tối ưu cho bài
toán Steiner chỉ bao gồm các đoạn thẳng nối mà không có đường cong
nào cả. Mạng này phải liên thông và không có chu trình (do điều kiện tối
ưu của nó, nếu có chu trình ta có bỏ bớt một cạnh trên chu trình mà không
ảnh hưởng tới sự liên thông của đồ thị). Như vậy, mạng tối ưu của bài
toán Steiner phải là một cây mà cạnh của nó là các đoạn thẳng. Ta gọi
mạng tối ưu trong bài toán Steiner là cây Steiner.
2. Phân tích bài toán Steiner cho n = 4 điểm
Nghiệm của bài toán Steiner là một hệ thống các đoạn thẳng nối các điểm
đã cho với các điểm Steiner ta thêm vào, cho nên chúng ta không thể nêu
quy luật tổng quát để xác định chính xác đó là các điểm nào và các đoạn
thẳng đó được nối như thế nào. Để đi tới phương pháp tổng quát, ta giải
bài toán cho trường hợp n = 4 điểm. Hơn thế nữa, ta chọn 4 điểm đó là 4
đỉnh của một hình vuông cạnh 1 để dễ giải.
4
Bài toán 1: Hãy dụng một mạng lưới giao thông nối 4 đỉnh của một hình
vuông ABCD cạnh 1 với tổng độ dài nhỏ nhất, sao cho từ một đỉnh tùy ý
của hình vuông, ta có thể đi theo các cạnh tới các đỉnh còn lại của hình
vuông.
Trong quá trình tìm kiếm mạng tối ưu, ta sẽ sử dụng định lí 11 quen biết
sau:
Định lí 1.
Trên mặt phẳng có một tam giác đều ABC và một điểm M. Khi đó ta có
bất đẳng thức MB + MC MA, với đẳng thức chỉ khi M nằm trên cung
BC của đường tròn ngoại tiếp tam giác ABC.
Định lí 11 trên có thể chứng minh dễ dàng nhờ định lí Prômêtê mở rộng,
được phát biểu như sau:
Định lí 2. Cho trước 4 điểm ABCD, khi đó ta có bất đẳng thức
AB.CD + AD.BC AC.BD,
đẳng thức xảy ra chỉ khi ABCD là một tứ giác nội tiếp.
Ta thấy rằng mạng tối ưu của chúng ta phải là một cây chứa các đỉnh của
hình vuông ABCD đã cho. Bây giờ chúng ta xem xét bài toán theo số các
điểm Steiner:
 Nếu chỉ có không có điểm Steiner nào cả:
5