Ph−¬ng ph¸p Gauss - Seidel vμ c«ng thøc
nhiÖt trë ph©n tè gi¶i c¸c bμi to¸n
nhiÖt kÕt cÊu c«ng tr×nh
PGS. TS. TrÞnh v¨n quang
KS. Tr−¬ng Minh th¾ng
Bé m«n Kü ThuËt NhiÖt
Khoa C¬ khÝ - Tr−êng §¹i häc GTVT
Tãm t¾t: Bμi b¸o tr×nh bμy mét ph−¬ng ph¸p gi¶i c¸c bμi to¸n nhiÖt phøc t¹p khi ph−¬ng
ph¸p ma trËn nghÞch ®¶o trë nªn bÊt lùc, ®ã lμ ph−¬ng ph¸p Gauss - Seidel vμ c«ng thøc nhiÖt
trë ph©n tè.
Summary: The paper presents the method of Gauss - Seidel Iteration to solve the
complicated thermal problems instead of the inverse matrix method becoming powerless.
i. ®Æt vÊn ®Ò
Mét trong c¸c ph−¬ng ph¸p cã hiÖu lùc
®Ó gi¶i c¸c bµi to¸n nhiÖt cña c¸c vËt thÓ cã
h×nh d¸ng vµ ®iÒu kiÖn biªn phøc t¹p lµ
ph−¬ng ph¸p sè dïng ma trËn nghÞch ®¶o. Khi
®ã c¸c nhiÖt ®é ph¶i t×m n»m trong mét hÖ
ph−¬ng tr×nh tuyÕn tÝnh, vµ ®−îc gi¶i b»ng
thuËt to¸n ma trËn [3]. Tuy nhiªn khi sè
ph−¬ng tr×nh qu¸ lín th× ph−¬ng ph¸p ma trËn
nghÞch ®¶o còng hÕt søc phøc t¹p. §Æc biÖt
tr−êng hîp ®iÒu kiÖn biªn kh«ng tuyÕn tÝnh,
nh− vËt thÓ cã trao ®æi bøc x¹ víi nguån cã
nhiÖt ®é x¸c ®Þnh, th× hÖ ph−¬ng tr×nh c¸c
nhiÖt ®é cÇn t×m kh«ng cßn lµ tuyÕn tÝnh n÷a
nªn ph−¬ng ph¸p ma trËn nghÞch ®¶o còng trë
nªn bÊt lùc. VËy cã thÓ gi¶i c¸c bµi to¸n trong
tr−êng hîp nµy nh− thÕ nµo.
Bµi b¸o tr×nh bµy ph−¬ng ph¸p Gauss -
Seidel vµ c«ng thøc nhiÖt trë ph©n tè ®Ó gi¶i
c¸c bµi to¸n phøc t¹p thuéc lo¹i nµy.
ii. c«ng thøc nhiÖt trë ph©n tè,
ph−¬ng ph¸p gauss - seildel
A. C«ng thøc nhiÖt trë ph©n tè
Khi x¸c ®Þnh nhiÖt ®é trong vËt thÓ b»ng
ph−¬ng ph¸p c©n b»ng n¨ng l−îng ph©n tè
cÇn tÝnh c¸c dßng nhiÖt ®Õn ph©n tè, trong ®ã
lu«n cã mÆt c¸c nhiÖt trë thµnh phÇn. §Ó
thuËn tiÖn cho tÝnh to¸n cã thÓ x©y dùng c«ng
thøc nhiÖt trë thµnh phÇn d¹ng tæng qu¸t sau.
1. Bμi to¸n æn ®Þnh
a. §iÒu kiÖn biªn lo¹i 1
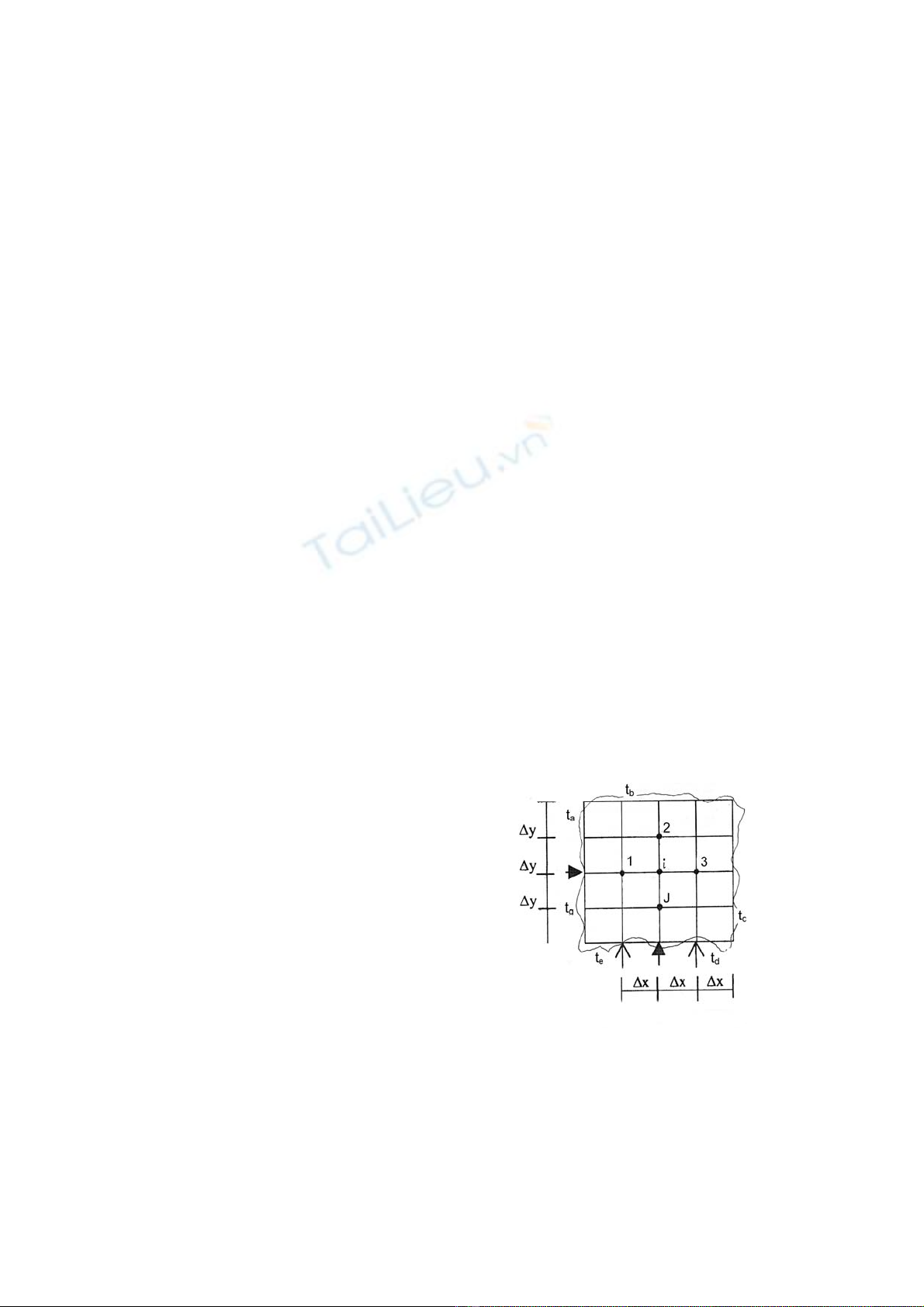
XÐt mét h×nh ph¼ng dµy 1m cho biÕt
nhiÖt ®é t¹i biªn giíi (h×nh 1).
H×nh 1. M¹ng c¸c ®iÓm nót
Chia h×nh ph¼ng bëi mét m¹ng c¸c
®−êng vu«ng gãc cã b−íc m¹ng Δx, Δy, øng
víi hai chiÒu x, y. Do æn ®Þnh, nhiÖt ®é t¹i mäi
®iÓm trong vËt kh«ng thay ®æi theo thêi gian
nªn tæng dßng nhiÖt ph©n tè nhËn ®−îc do
dÉn nhiÖt tõ xung quanh ®Õn b»ng kh«ng
(h×nh 2). Khi ®ã ph−¬ng tr×nh n¨ng l−îng t¹i
mçi ph©n tè t¹i ®iÓm nót i:
Σqi = 0 (1)
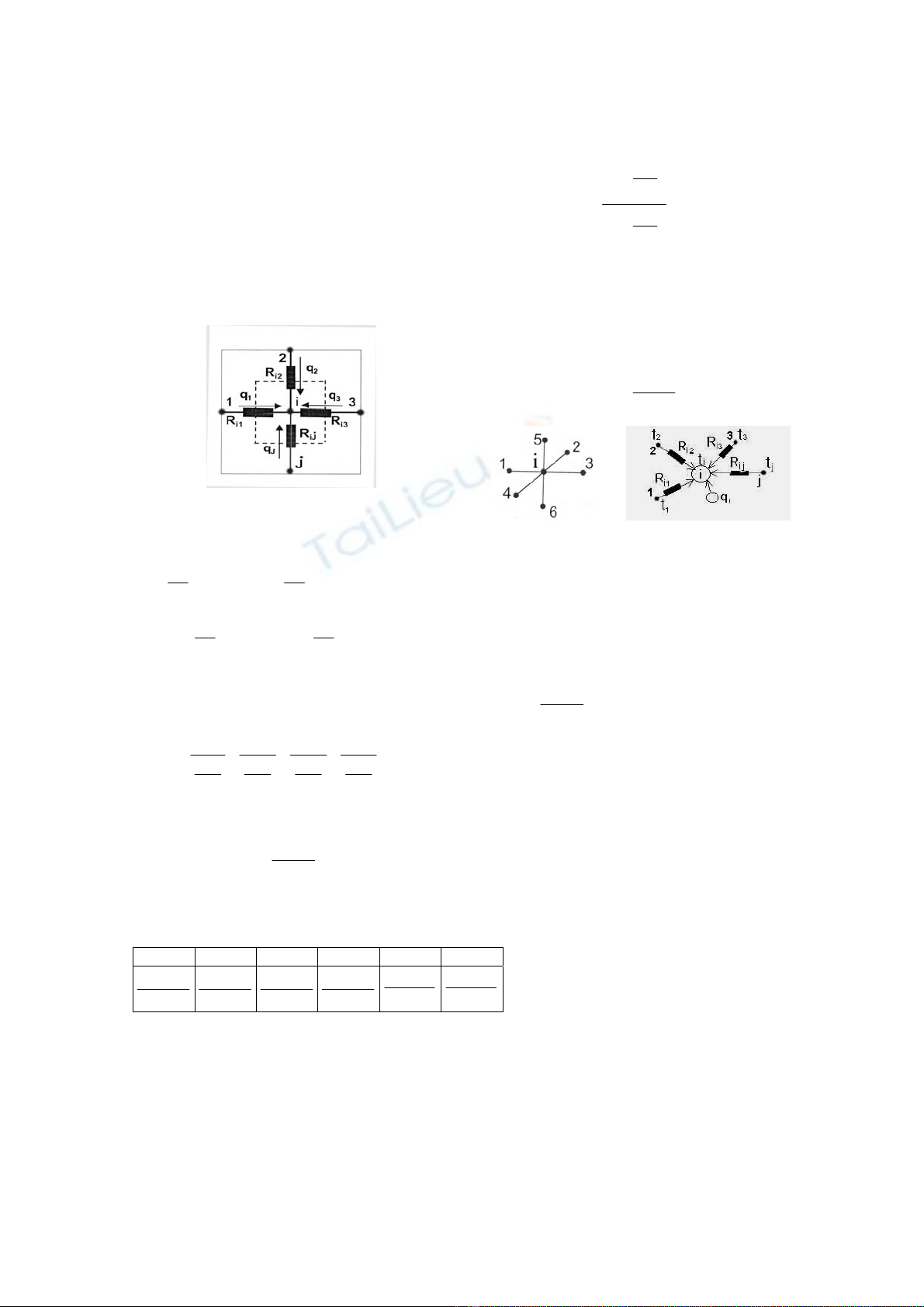
H×nh 2. C¸c nhiÖt trë thμnh phÇn t¹i nót i
dÉn tíi:
+Δ−
Δ
λ
+Δ−
Δ
λ1.y)tt(
x
1.y)tt(
xi3i1
01.x)tt(
y
1.x)tt(
yiJi2 =Δ−
Δ
λ
+Δ−
Δ
λ
+
(2)
Hay:
0
x.
y
tt
x.
y
tt
y.
x
tt
y.
x
tt iJi2i3i1 =
Δλ
Δ
−
+
Δλ
Δ
−
+
Δλ
Δ
−
+
Δλ
Δ
− (3)
ViÕt ë d¹ng tæng qu¸t:
∑=
−
jiJ
iJ 0
R
tt (4)
NhiÖt trë thµnh phÇn trong bµi to¸n ba
chiÒu trong to¹ ®é xyz sÏ cã J = 1 ÷ 6 (h×nh 3):
Trong ®ã tJ lµ nhiÖt ®é c¸c ®iÓm xung
quanh, ti lµ nhiÖt ®é ph¶i t×m t¹i nót i; RiJ ®−îc
gäi lµ c«ng thøc nhiÖt trë ph©n tè.
Tõ ®ã tÝnh ®−îc nhiÖt ®é ti:
∑
∑⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
JiJ
JiJ
J
i
R
1
R
t
t (6)
b. §iÒu kiÖn biªn lo¹i 2, 3:
T¹i nót ë biªn cã c¸c dßng nhiÖt ®èi l−u
hoÆc bøc x¹ vµ dÉn nhiÖt tõ c¸c ph©n tè bªn
(h×nh 4):
0
R
tt
q
JiJ
iJ
i
i=
−
+∑∑ (7)
H×nh 3. M¹ng 3 chiÒu H×nh 4. C¸c nhiÖt trë
thμnh t¹i nót i t¹i biªn
trong ®ã:
-
∑
i
i
qlµ tæng c¸c dßng nhiÖt bøc x¹
hoÆc ®èi l−u tíi ph©n tè.
- ∑−
JiJ
iJ
R
tt lµ tæng c¸c dßng nhiÖt dÉn tõ
ph©n tè bªn c¹nh tíi.
NÕu theo h−íng x, t¹i biªn cã dßng nhiÖt
®èi l−u vµ bøc x¹, th× dßng nhiÖt ®èi l−u lµ:
qi = α(tK -ti)ΔyΔz;
NhiÖt trë ®èi l−u lµ: Ri =1/ αΔyΔz
Dßng nhiÖt bøc x¹ lµ:
qi = ε.σ0.
(
)
4
i
4
RTT −ΔyΔz;
Ri1 Ri2 Ri3 Ri4 Ri5 Ri6 NhiÖt trë bøc x¹ lµ:
Ri = 1/ [ ε.σ0.
(
)
2
i
2
RTT +
(
)
iR TT +ΔyΔz]
trong ®ã:
- tK, ti lµ nhiÖt ®é m«i tr−êng vµ t¹i nót i;
- TR, Tl lµ nhiÖt ®é tuyÖt ®èi cña nguån
λΔΔ
Δ
.z.y
x λΔΔ
Δ
.z.x
y λΔΔ
Δ
.z.y
x λΔΔ
Δ
.z.x
y λΔΔ
Δ
.y.x
z
λΔΔ
Δ
.y.x
z
(
5
)

bøc x¹ vµ cña nót i;
- ε ®é ®en cña vËt;
- σ0 = 5,669.10 - 8
NhiÖt ®é t¹i nót i sÏ lµ:
∑
∑∑ ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
=
JiJ
JiJ
J
i
i
i
R
1
R
t
q
t (8)
Nh− vËy thÊy r»ng c«ng thøc nhiÖt trë
ph©n tè lu«n cã mÆt khi tÝnh nhiÖt ®é.
2. Bµi to¸n kh«ng æn ®Þnh
a. §iÒu kiÖn biªn lo¹i 1
Víi bµi to¸n kh«ng æn ®Þnh t¹i mçi nót i
sÏ cã: Tæng n¨ng l−îng ph©n tè nhËn ®−îc tõ
xung quanh b»ng ®é t¨ng néi n¨ng cña ph©n
tè trong mét ®¬n vÞ thêi gian:
∑τΔ
−
=
−+
j
p
i
1p
i
i
iJ
p
i
p
jtt
.C
R
tt (9)
trong ®ã:
- p lµ sè chØ thø tù b−íc thêi gian
- ∑−
jiJ
p
i
p
j
R
tt lµ tæng c¸c dßng nhiÖt tíi
ph©n tè t¹i thêi ®iÓm p; Ci lµ nhiÖt dung ph©n
tè: Ci =c.ρ.ΔxΔyΔz (j/®é);
- RiJ lµ nhiÖt trë thµnh phÇn cña ph©n tè;
j sè thø tù c¸c nót kÒ bªn.
Tõ ®ã rót ra nhiÖt ®é t¹i mçi nót t¹i thêi
®iÓm p +1:
P
i
JiJii
JiJ
P
J
1P
it.
R
1
C
1
CR
t
t⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛τΔ
−+
τΔ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=∑∑
+ (10)
C«ng thøc (9) tÝnh nhiÖt ®é ë d¹ng hµm
t−êng, ®Ó nghiÖm æn ®Þnh cÇn ®iÒu kiÖn sè
h¹ng sau vÕ ph¶i cña (9) ph¶i kh«ng ©m, tõ
®ã ph¶i chän b−íc thêi gian tho¶ m·n ®iÒu
kiÖn:
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
≤τΔ ∑
JiJ
i
R
1
C (11)
b. §iÒu kiÖn biªn lo¹i 2, 3
T¹i biªn cã ®èi l−u hoÆc bøc x¹ kÕt hîp
(7) vµ (9) sÏ cã ph−¬ng tr×nh n¨ng l−îng t¹i
ph©n tè thuéc nót i:
∑∑ τΔ
−
=
−
+
+
j
p
i
1p
i
i
iJ
p
i
p
j
i
i
tt
.C
R
tt
q (12)
Tõ ®ã rót ra ®−îc nhiÖt ®é t¹i nót i ë thêi
®iÓm p + 1:
P
i
JiJii
JiJ
P
J
i
i
1P
it.
R
1
C
1
CR
t
qt ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛τΔ
−+
τΔ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+= ∑∑∑
+
(13)
§iÒu kiÖn æn ®Þnh còng nh− c«ng thøc
(11) trªn.
Nh− vËy cã thÓ thÊy trong mäi tr−êng hîp
®Ó tÝnh nhiÖt ®é lu«n cÇn tíi c«ng thøc nhiÖt
trë ph©n tè, vµ khi ®ã viÖc tÝnh to¸n sÏ trë nªn
thuËn tiÖn vµ gän gµng h¬n.
B. Ph−¬ng ph¸p Gauss - Seidel
Néi dung c¬ b¶n cña ph−¬ng ph¸p nµy lµ
c¸ch tÝnh lÆp. Tõ c¸c ph−¬ng tr×nh tÝnh nhiÖt
®é trong c¸c tr−êng hîp trªn, thÊy r»ng nhiÖt
®é t¹i mçi nót ë d¹ng hµm t−êng cu¶ nhiÖt ®é
cña c¸c nót cßn l¹i ®èi víi bµi to¸n æn ®Þnh, vµ
lµ hµm t−êng cña nhiÖt ®é cña c¸c nót cßn l¹i
ë thêi ®iÓm tr−íc ®èi víi bµi to¸n kh«ng æn ®inh.
NghÜa lµ cã n ph−¬ng tr×nh ®Ó tÝnh n nhiÖt ®é ph¶i
t×m. Bëi vËy ph−¬ng ph¸p Gaus- Seidel bao gåm
c¸c b−íc sau:
1. LËp hÖ ph−¬ng tr×nh nhiÖt ®é d¹ng
hµm t−êng cho c¸c nót.
2. Trõ mét nhiÖt ®é t¹i nót 1 (hoÆc nót m
nµo ®ã ®Þnh tÝnh tr−íc tiªn), tÊt c¶ nhiÖt ®é t¹i
c¸c nót cßn l¹i cho gi¸ trÞ ban ®Çu tio bÊt kú,
còng cã thÓ cho b»ng kh«ng (tio = 0).

3. Thay c¸c gi¸ trÞ tio ®· cho vµo ®Ó tÝnh
ra nhiÖt ®é t1 t¹i nót 1 (hoÆc m).
4. Thay t1 míi nhËn ®−îc vµo c¸c ph−¬ng
tr×nh cßn l¹i, tÝnh dÇn ra c¸c nhiÖt ®é ë c¸c nót
tiÕp theo. Khi ®−îc mét gi¸ trÞ nhiÖt ®é míi
ph¶i sö dông ngay trong c¸c ph−¬ng tr×nh cßn
l¹i. NghÜa lµ mäi ph−¬ng tr×nh lu«n ph¶i nhËn
®−îc gi¸ trÞ míi nhÊt nÕu cã, cho ®Õn ph−¬ng
tr×nh cuèi cïng.
5. Qu¸ tr×nh tÝnh ®−îc tÝnh lÆp l¹i lÇn 2,
lÇn 3 ... víi c¸c gi¸ trÞ nhiÖt ®é míi nhÊt.
6. Qu¸ tr×nh tÝnh lÆp sÏ ®−îc dõng khi
nµo chªnh lÖch nhiÖt ®é t¹i mäi ®iÓm ë hai lÇn
tÝnh s¸t nhau nhá tíi møc ®ñ chÊp nhËn.
Víi sù trî gióp cña c¸c phÇn mÒm tÝnh
to¸n hiÖn nay, viÖc tÝnh theo ph−¬ng ph¸p
Gauss - Seidel rÊt thuËn tiÖn.
C. ThÝ dô minh ho¹
+ ThÝ dô 1: Gi¶i bµi to¸n æn ®Þnh hai chiÒu
®iÒu kiÖn biªn
lo¹i 1:
Mét dÇm
bªt«ng, tiÕt diÖn
ngang cã h×nh
d¹ng nh− h×nh
bªn cã Δx = Δy.
BiÕt nhiÖt ®é t¹i c¸c c¹nh vµ gãc cña tiÕt diÖn
nh− trªn h×nh vÏ. X¸c ®Þnh nhiÖt ®é t¹i c¸c
®iÓm bªn trong 1, 2, 3, 4, 5, 6.
Gi¶i:
Do Δx = Δy, theo (4) c¸c nhiÖt trë thµnh
phÇn cña mäi ph©n tè ®Òu b»ng nhau lµ
R
ij = 1/λ, nªn tõ (5) sÏ cã:
tij =
()
4i3i2i1i tttt
4
1+++
B−íc 1: T¹i c¸c ®iÓm 1, 2, 3, 4, 5, 6 viÕt
®−îc 6 ph−¬ng tr×nh nhiÖt ®é d¹ng hµm t−êng
sau:
t1 = (t2 + 60 + 100 +50 ) / 4 (a)
t2 = (t1 + t3 + t5 + 100 ) / 4 (b)
t3 = (t2 + t4 + t6 + 100 ) / 4 (c)
t4 = (t3 + 100 + 80 +70 ) / 4 (d)
t5 = (t2 + t6 + 50 + 40 ) / 4 (e)
t6 = (t3 + t5 + 70 + 40 ) / 4 (g)
B−íc 2: Cho t2 = 0; t3 = 0; t4 = 0; t5 = 0;
t6 = 0;
B−íc 3: Thay t2 = 0 vµo (a) tÝnh ®−îc
t1 = 52, 50.
B−íc 4: Thay t1 = 52,5 (gi¸ trÞ míi) vµ
t3 = 0; t5 = 0 vµo (b) tÝnh ®−îc t2 = 38,125 ...
tiÕp tôc nh− vËy sÏ tÝnh ®−îc t3; t4; t5; t6 thø tù
nh− sau: 52.5000 38.1250 34.5313 71.1328
32.0313 44.1406.
B−íc 5: KÕt qu¶ tÝnh lÆp sau 8 lÇn viÕt
theo ma trËn hµng t = [t1 t2 t3 t4 t5 t6] nh− sau:
(1) 52.5000 38.1250 34.5313 71.1328 32.0313 44.1406
(2) 62.0313 57.1484 68.1055 79.5264 47.8223 56.4819
H×nh 5. Chia m¹ng tiÕt diÖn
ngang dÇm bªt«ng
(3) 66.7871 70.6787 76.6718 81.6679 54.2902 60.2405
(4) 70.1697 75.2829 79.2978 82.3245 56.3808 61.4197
(5) 71.3207 76.7498 80.1235 82.5309 57.0424 61.7915
(6) 71.6875 77.2133 80.3839 82.5960 57.2512 61.9088
(7) 71.8033 77.3596 80.4661 82.6165 57.3171 61.9458
(8) 71.8399 77.4058 80.4920 82.6230 57.3379 61.9575
B−íc 6: Sai sè tuyÖt ®èi 2 lÇn cuèi t−¬ng
øng lµ: 0.0366 0.0462 0.0259 0.0065
0.0208 0.0117 lµ qu¸ nhá nªn cã thÓ dõng
phÐp tÝnh lÆp.
NÕu tÝnh theo ph−¬ng ph¸p ma trËn
nghÞch ®¶o, nhiÖt ®é c¸c ®iÓm t−¬ng øng sÏ
lµ: 71.8630 77.4380 80.5120 82.6310
57.3340 61.9500.
C¸c bµi to¸n thùc tÕ cã sè nhiÖt ®é ph¶i
t×m lªn tíi hµng tr¨m th× ph−¬ng ph¸p ma trËn
nghÞch ®¶o rÊt phøc t¹p, khi ®ã ph−¬ng ph¸p
Gauss - Seidel tá râ −u thÕ h¬n rÊt nhiÒu.
+ ThÝ dô 2: Gi¶i bµi to¸n kh«ng æn ®Þnh
t¹i biªn cã nguån bøc x¹ víi nhiÖt ®é x¸c ®Þnh.
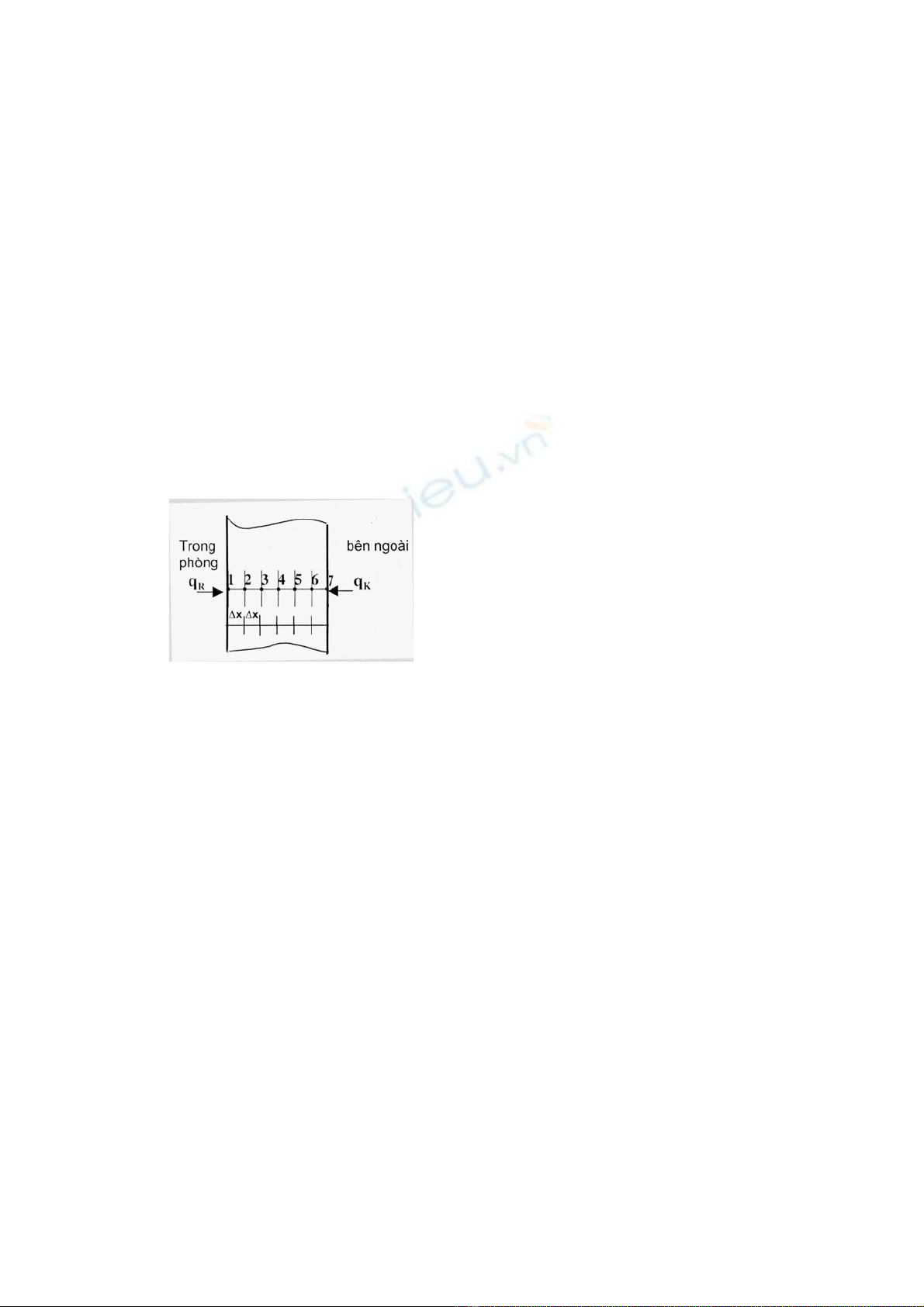
T−êng mét c¨n phßng lµm viÖc cã bÒ dµy
30 cm, chiÒu cao kh¸ lín 6m. T−êng cã c¸c
th«ng sè nhiÖt: hÖ sè dÉn nhiÖt λ = 2,5 W/m ®é,
nhiÖt dung riªng c = 800 J/kg ®é, khèi l−îng riªng
ρ = 1800 kg/m3, ®é ®en ε = 0,65. NhiÖt ®é ban
®Çu mÆt t−êng bªn trong phßng lµ 270C, bªn
ngoµi tiÕp xóc víi kh«ng khÝ mÆt t−êng cã
nhiÖt ®é 350C. HÖ sè to¶ nhiÖt cña t¹i mÆt
ngoµi t−êng α = 25 W/m2®é. Bçng c¨n phßng
®ét ngét bÞ ch¸y, nhiÖt ®é ngän löa trong
phßng lªn tíi 10000C. §Ó ®¸nh gi¸ tr¹ng th¸i
ph¸ huû cña t−êng phßng, cÇn ph¶i x¸c ®Þnh
diÔn biÕn ph©n bè nhiÖt ®é cña t−êng. §©y
còng lµ bµi to¸n ch¸y c¬ b¶n trong c«ng tr×nh
x©y dùng.
H×nh 6. Chia líp t−êng phßng
Gi¶i: Do chiÒu cao t−êng rÊt lín so víi
bÒ dµy nªn dßng nhiÖt truyÒn theo h−íng bÒ
dµy x lµ chÝnh. Khi ®ã bµi to¸n lµ mét chiÒu
kh«ng æn ®Þnh t = f(x,τ). Chia bÒ dµy t−êng
thµnh 6 líp, mçi líp cã Δx = 0,05m. Bªn tr¸i lµ
trong phßng cã nhiÖt ®é cao, t−êng nhËn bøc
x¹ qR lµ chÝnh, bá qua ®èi l−u. Bªn ph¶i lµ
ngoµi trêi nhiÖt ®é thÊp nªn chØ kÓ ®Õn ®èi l−u
qK mµ kh«ng tÝnh bøc x¹.
¸p dông ®iÒu kiÖn æn ®Þnh (10), tÝnh Δτ
t¹i c¸c ®iÓm 1 ÷ 7 nh− sau:
TÝnh Ci:
Ci = CρΔVi; C1 = 800.1800.0,05/2 = 36000;
C2 = 800.1800.0,05 = 72000; C3 = C4 = C5 = C6;
C7 = C1;
TÝnh Δτi:
§iÓm 1:
Σ(1/R1j) = ε.σ0.
(
)
2
1
2
RTT +
(
)
1R TT + + λ/Δx
= 0,65×5,67×10-8×(12732+3002)×
× (1273 + 300)+2,5/0,05
= 149,1643;
vËy Δτ1 ≤ 3600/149,1643 = 241,3446s;
§iÓm 2, .., 6:
Σ(1/R2j) = λ/Δx + λ/Δx
= 2×(2,5/0,05) = 100;
VËy Δτ2 ≤ 7200/100 = 720s;
Δτ3 = Δτ4 = Δτ5 = Δτ6 = Δτ2 = 720s.
§iÓm 7:
Σ(1/R7j) = α + λ/Δx = 25 + 50 = 75;
cã Δτ7 ≤ 3600/75 = 480s;
Nh− vËy chØ cÇn chän Δτmax = 240 s lµ ®ñ.
Tuy nhiªn ®Ó phÐp tÝnh cã møc chÝnh x¸c ®ñ
cao, chän Δτmax = 120 s. Tõ (13) x¸c ®Þnh ®−îc
ph−¬ng tr×nh nhiÖt ®é tuyÖt ®èi t¹i c¸c ®iÓm:
§iÓm 1:
++−= −+ p
2
4P
1
101P
1T.16666,0)T.(10.2285,1T
(14)
6181,322T.8334,0 P
1++
§iÓm 2, 3, .. ,6 (i = 2..6):
p1i
P
i
p1i
1P
iT.08333,0T.8333,0T.08333,0T +−
+++=
(15)
§iÓm 7:
6564,25T.75001,0T.16666,0T P
7
p
6
1P
7++=
+
(16)
Sau khi lÊy gi¸ trÞ nhiÖt ®é ban ®Çu
(p = 1) n»m trªn ®−êng th¼ng gi÷a hai
nhiÖt ®é 300K vµ 308K, thay vµo c¸c ph−¬ng
tr×nh (14), (15), (16), tÝnh ®−îc nhiÖt ®é t¹i c¸c
vÞ trÝ sau 50 thêi ®iÓm. Ph©n bè nhiÖt ®é trong
t−êng t¹i c¸c thêi ®iÓm trªn ®−îc biÓu diÔn
trªn ®å thÞ, h×nh 7.
P
i
T
(Xem tiÕp trang 39)
















