ĐỀ THI HỌC SINH GIỎI LỚP 12
Môn thi: Toán
Thời gian làm bài: 180 phút
CâuI : (4 điểm):
Cho hàm số y= x3 + 3x2 - 2 (C)
1/ Khảo sát và vẽ đồ thị.
2/ Giải bất phương trình : 0 2006 + 6018x2- 4012 4012.
3/ Viết phương trình tiếp tuyến của đồ thị (C). Biết tiếp tuyến đi qua A(0; -2)
CâuII : (2 điểm) Tính
I= 1
x
e
dx
CâuIII : (2 điểm) Giải và biện luận phương trình theo tham số m
mxx 11
Câu IV: (4 điểm) Giải các phương trình sau:
1/ Sin(/2 - cosx)= cos(3cosx)
2/ 6x + 4x = 2.9x
Câu V : (2 điểm) Chứng minh điều kiện cần và đủ để tam giác ABC vuông:
Cos2A + Cos2B + Cos2C = 1
Câu VI: (2 điểm): Tính giới hạn sau:
2
23 2
0
927279
lim
x
xx
x
Câu VII: (2 điểm): Trong hệ Oxy cho hai đường thẳng d1//d2 lần lượt có
phương trình là :
d1: x-y+2 = 0 ; d2: x-y-2 = 0
1/ Viết phương trình đường thẳng d3 đi qua điểm A(-2; 0) và vuông góc với
d2
2/ Viết phương trình đường thẳng d4 sao cho d1, d2, d3, d4 cắt nhau tạo thành
một hình vuông.
Câu XIII: (2 điểm): Chứng minh rằng với a,b> 0 ta có:
a5+b5 a4b + ab4
KỲ THI HỌC SINH GIỎI LỚP 12
HƯỚNG DẪN CHẤM THI
Môn: Toán- Đề 2
(Bản hướng dẫn chấm gồm 5 trang)
Câu 1: (4 điểm)
1, (2 điểm)
TXĐ : D = R (0,25đ)
Chiều biến thiên: (0,5đ)
+ y' = 3x2 + 6x = 3x(x+2), y' = 0
2
0
x
x
+ dấu y':
x - -2 0 +
y' + 0 - 0 +
2 +
y
- -2
Với x(-; -2) (0; +) hàm số đồng biến
x(-2; 0) hàm số nghịch biến
Tại x= -2 hàm số đạt cực đại yCĐ = 2
Tại x= 0 hàm số đạt cực tiểu yCT = -2 (0,25đ)
Tính lồi lõm, điểm uốn. (0,25đ)
+ y'' = 6x + 6 = 6(x+1); y'' = 0 x= -1
+ dấu y'':
x -
-1 +
y'' -
0
+
đ.u
y L
ồi
(-1,0)
lõm
Bảng biến thiên: (0,25đ)
x - -2 -1 0 +
y' + 0 0 +
2 +
y (CĐ)
0 (CT)
- -2
x
y
01
2
-2
-1-
3
3
-1+ 3
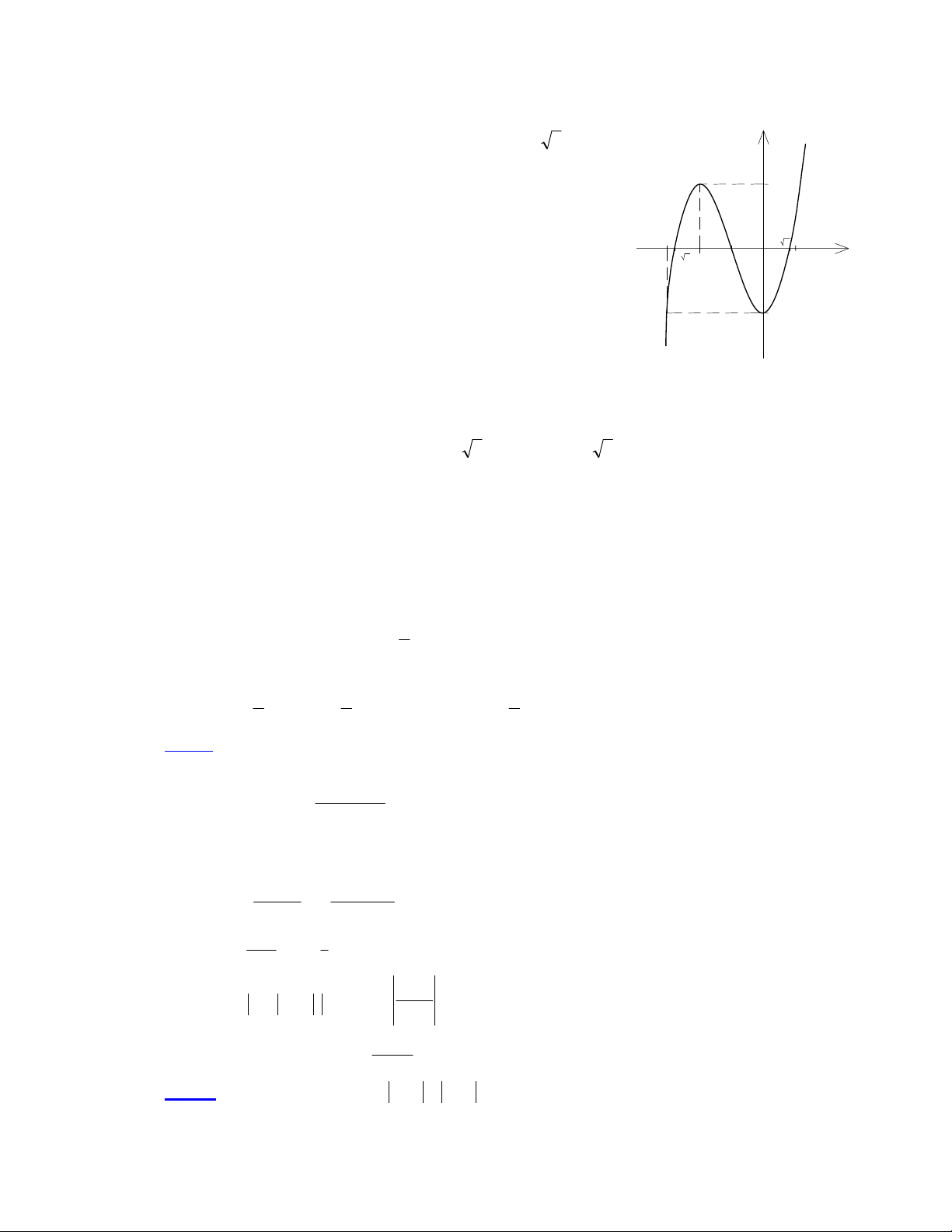
* Đồ thị: Đồ thị cát trục tung tại: (0; -2)
* Cắt trục hoành tại hoành độ x = -1, x = 31
Qua điểm (-3; -2); (1; 2)
2. (1 điểm)
0
2006 x3 + 6018 x2 - 4012
4012
0
x3 + 3x2 - 2
2 (*) (0,5đ)
theo đồ thị (C) ta có: (*)
x
[ -1- 3; -1 ]
[ -1+ 3; 1 ] (0,5đ)
3. (1 điểm): đường thẳng qua A(0; -2) có hệ số góc k:
y+2= k(x- 0) (d) y = kx-2
(d) là tiếp tuyến của (c)
xxk
kxxx
xxk
kxxx
63
)1(3
63
223 3
2
23 (0,5đ)
có nghiệm.
Thay k từ (2) vào (1) ta được:
x2(2x+3) = 0
x = 0, x= -
2
3 (0,25đ)
* Với x= 0
k= 0 tiếp tuyến là y = - 2
* Với x= -
2
3
k= -
4
9 tiếp tuyến là y= - 2
4
9x (0,25đ)
Câu 2 (2 điểm).
1. (1 điểm)
Ta có I = )1( xx
x
ee
dxe
Đặt ex+1 = t (*) ex = t-1
exdx = dt
I= dt
tt
tt
tt
dt
)1(
)1(
)1(
= dt
t
dt
t
1
1
1 (0,5đ)
=ln 1t- ln t +c =ln t
t1 +c
Từ (*) ta có: I = ln
1
x
x
e
e + c = x - ln(ex +1) +c (0,5đ)
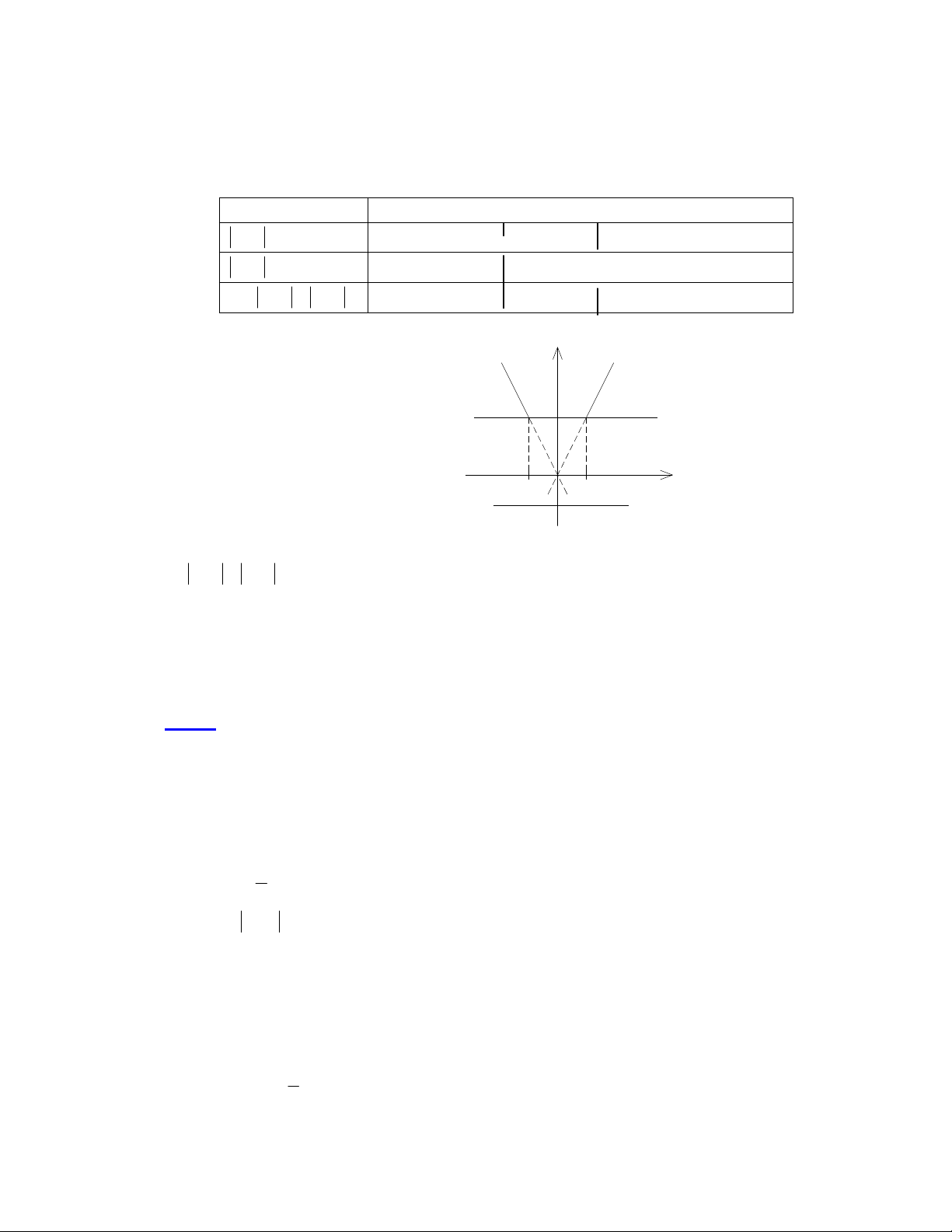
Câu 3. (2đ) Xét hàm số y= 11 xx (c)
0,5
đ
Ta có bảng xét dấu (1đ)
x -
-1
1
1x -x-1 0 x+1 x+1
1x -x+1 -x+1 0 x-1
y= 11 xx -2x 2 2x
Khi đó y=
x
x
2
2
2
1
11
1
x
x
x
đồ thị (C)
* Biện luận số nghiệm của phương trình theo m:
11 xx = m (*) (0,5đ)
số nghiệm của phương trình (*) là số giao điểm của đồ thị (C) với đường thẳng
y = m
+ Nếu m<2 phương trình vô nghiệm
+ Nếu m=2 phương trình có nghiệm [1; 1]
+ Nếu m>2 phương trình có 2 nghiệm phân biệt.
Câu 4 (4đ)
1. Phương trình tương đương với :
Cos (
cosx) = cos 3
cosx (0,25đ)
23
23
kCosxCosx
kCosxCosx (k
Z
)
kCosxCosx
kCosxCosx
23
23 (0,5đ)
)2(
2
)1(
k
Cosx
kCosx
(0,25đ)
Vì k
Z, 1Cosx nên:
(1) (*)
1
0
Cosx
Cosx (0,25đ)
(2)
2
1
1
0
Cosx
Cosx
Cosx
(**) (0,25đ)
Nếu
Nếu
Nếu
y = 2
y = m
2
-1
1
x
y
(0,5đ)
(C)
Từ (*) và (**) ta có:
)5(
2
1
)4(1
)3(0
Cosx
Cosx
Cosx
(0,25đ)
)(2
3
2
)(2
3
)5(
)()4(
)()3( 2
dkx
ckx
bkx
akx
Với (k
Z
). (0,5đ)
Từ (a),(b),(c),(d) ta có nghiệm của phương trình là :
23
22
k
x
k
x
(k
Z
) (0,25đ)
2. Phương trình tương đương với
2
3
2
3
22
xx
(1) (0,5đ)
Đặt t =
x
3
2Điều kiện t > 0. (0,25đ)
(1)
t2 + t -2 = 0
2
1
2
1
t
t
Với t = 1
x
3
2= 1
x
3
2=
0
3
2
(0,5đ)
x=0
Vậy phương trình có nghiệm x = 0. (0,25đ)
Câu 5 (2đ)
0
0
0
0..
0)()(
0)()(
1)22(
2
1
1
1
2
21
2
21
1
2
2
2
222
CosC
CosB
CosA
CosCCosBCosA
BACosBACosCosC
CCosBACosBACos
CCosBCosACos
CCos
BCosACos
CCosBCosACos
(0,25
đ
)
(0,25đ)
(0,25đ)
(0,25đ)
(0,25đ)
(0,25đ)
(0,25đ)
(Loại)