Nguyn Phú Khánh – à Lt
48
Bài 2: CC TR HÀM S
2.1 TÓM TT LÝ THUYT
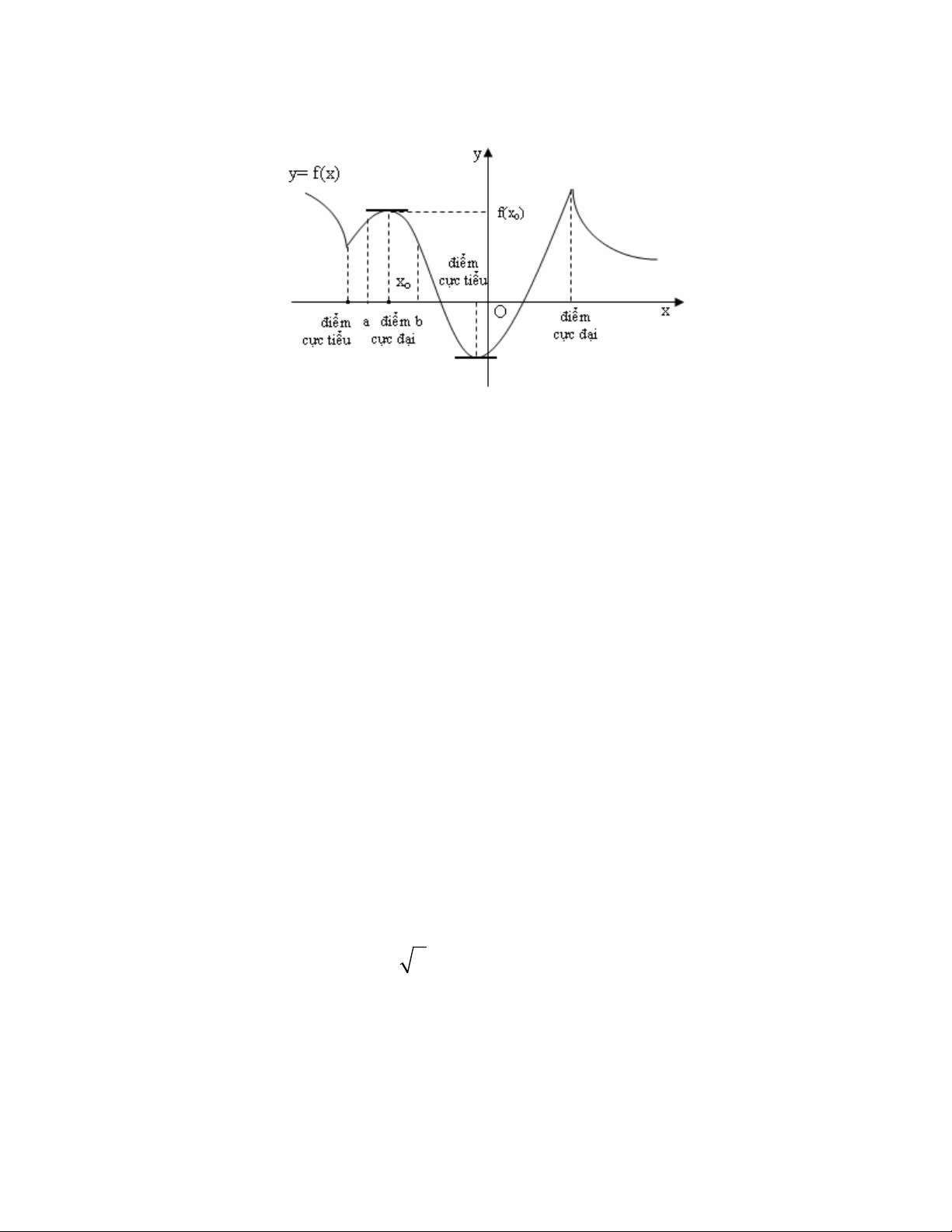
1. Khái nim cc tr hàm s :
Gi s hàm s
xác nh trên tp hp
(
)
⊂
và
∈
ưc gi là mt im cc i ca hàm s
nu tn ti mt khong
(
)
cha im
sao cho:
(
)
( ) { }

⊂
< ∀ ∈
. Khi ó
(
)
ưc
gi là giá tr cc i ca hàm s
.
ưc gi là mt im cc tiu ca hàm s
nu tn ti mt khong
(
)
cha im
sao cho:
(
)
( ) { }

⊂
< ∀ ∈
. Khi ó
(
)
ưc
gi là giá tr cc tiu ca hàm s
.
Giá tr cc i và giá tr cc tiu ưc gi chung là cc tr
Nu
là mt im cc tr ca hàm s
thì ngưi ta nói rng hàm s
t cc
tr ti im
.
Nh vy : im cc tr phi là mt im trong ca tp hp
(
)
⊂
Nhn mnh :
(
)
∈ ⊂ ngha là
là mt im trong ca
:
Ví d : Xét hàm s
=
xác nh trên
)
+∞
. Ta có
(
)
>
vi mi
>
nhưng
=
không phi là im cc tiu vì tp hp
)
+∞
không cha bt kì mt lân cn nào ca im
.
Nguyn Phú Khánh – à Lt
49
Chú ý :
•
Giá tr cc i ( cc tiu)
nói chung không phi là GTLN (GTNN) ca
trên tp hp
.
•
Hàm s có th t cc i hoc cc tiu ti nhiu im trên tâp hp
.
Hàm s cng có th không có im cc tr.
•
là mt im cc tr ca hàm s
thì im
(
)

ưc gi là im
cc tr ca  th hàm s
.
2. iu kin cn hàm s t cc tr:
nh lý 1: Gi s hàm s
t cc tr ti im
. Khi ó , nu
có o hàm
ti im
thì
(
)
=
Chú ý :
•
o hàm
có th bng
ti im
nhưng hàm s
không t cc tr ti
im
.
•
Hàm s có th t cc tr ti mt im mà ti ó hàm s không có o hàm
.
•
Hàm s ch có th t cc tr ti mt im mà ti ó o hàm ca hàm s
bng
, hoc ti ó hàm s không có o hàm .
•
Hàm s t cc tr ti
và nu  th hàm s có tip tuyn ti im
(
)

thì tip tuyn ó song song vi trc hoành.
Ví d : Hàm s
=
và hàm s
=
3. iu kin   hàm s t cc tr:
nh lý 2: Gi s hàm s
liên tc trên khong
(
)
cha im
và có o
hàm trên các khong
(
)
và
(
)
. Khi ó :
Nu
(
)
(
)
( ) ( )
< ∈
> ∈
thì hàm s t cc tiu ti im
. Nói mt
cách khác , nu
(
)
i du t âm sang dương khi
qua im
thì hàm s
t cc tiu ti im
.
(
)
−
+
(
)
(
)
(
)
(
)
Nguyn Phú Khánh – à Lt
50
Nu
(
)
(
)
( ) ( )
> ∈
< ∈
thì hàm s t cc i ti im
. Nói mt
cách khác , nu
(
)
i du t dương sang âm khi
qua im
thì hàm s
t cc i ti im
.
(
)
+
−
(
)
(
)
(
)
(
)
nh lý 3: Gi s hàm s
có o hàm cp mt trên khong
(
)
cha im
,
(
)
=
và
có o hàm cp hai khác
ti im
.
Nu
(
)

<
thì hàm s
t cc i ti im
.
Nu
(
)

>
thì hàm s
t cc tiu ti im
.
Chú ý:
Không c!n xét hàm s
có hay không có o hàm ti im
=
nhưng không
th b" qua iu ki#n " hàm s liên tc ti im
"
Ví d : Hàm s


− ≤
=
>
không t cc tr ti
=
. Vì
hàm s không liên tc ti
=
.
2.1 DNG TOÁN THƯNG GP.
Dng 1 : Tìm các im cc tr ca hàm s .
Quy tc 1: Áp dng nh lý 2
•
Tìm
(
)
•
Tìm các im
(
)

=
ti ó o hàm bng
hoc hàm s liên tc
nhưng không có o hàm.
Nguyn Phú Khánh – à Lt
51
•
Xét du ca
(
)
. Nu
(
)
i du khi
qua im
thì hàm s có cc
tr ti im
.
Quy tc 2: Áp dng nh lý 3
•
Tìm
(
)
•
Tìm các nghi#m
(
)

=
ca phương trình
(
)
=
.
•
Vi m$i
tính
(
)

−
Nu
(
)

<
thì hàm s t cc i ti im
.
−
Nu
(
)

>
thì hàm s t cc tiu ti im
.
Ví d 1 : Tìm cc tr ca các hàm s :

= + + +

= − + − +
Gii :

= + + +
Hàm s ã cho xác nh và liên tc trên
.
Ta có:
= + + = + ≥ ∀
Hàm s không có cc tr.
Chú ý:
* Nu
không i du thì hàm s không có cc tr.
* i vi hàm bc ba thì
=
có hai nghi#m phân bi#t là iu c!n và  
hàm có cc tr.

= − + − +
Hàm s ã cho xác nh và liên tc trên
.
Ta có:

= − + − = − − +
= ⇔ − − + = ⇔ = ∨ = −
Bng bin thiên
−∞
−
+∞
+
+
−
−∞

−∞
Vy, hàm t cc i ti
= −
vi giá tr cc i ca hàm s là

− =
,
hàm s không có cc tiu.
Bài tp t luyn:
Tìm cc tr ca các hàm s :
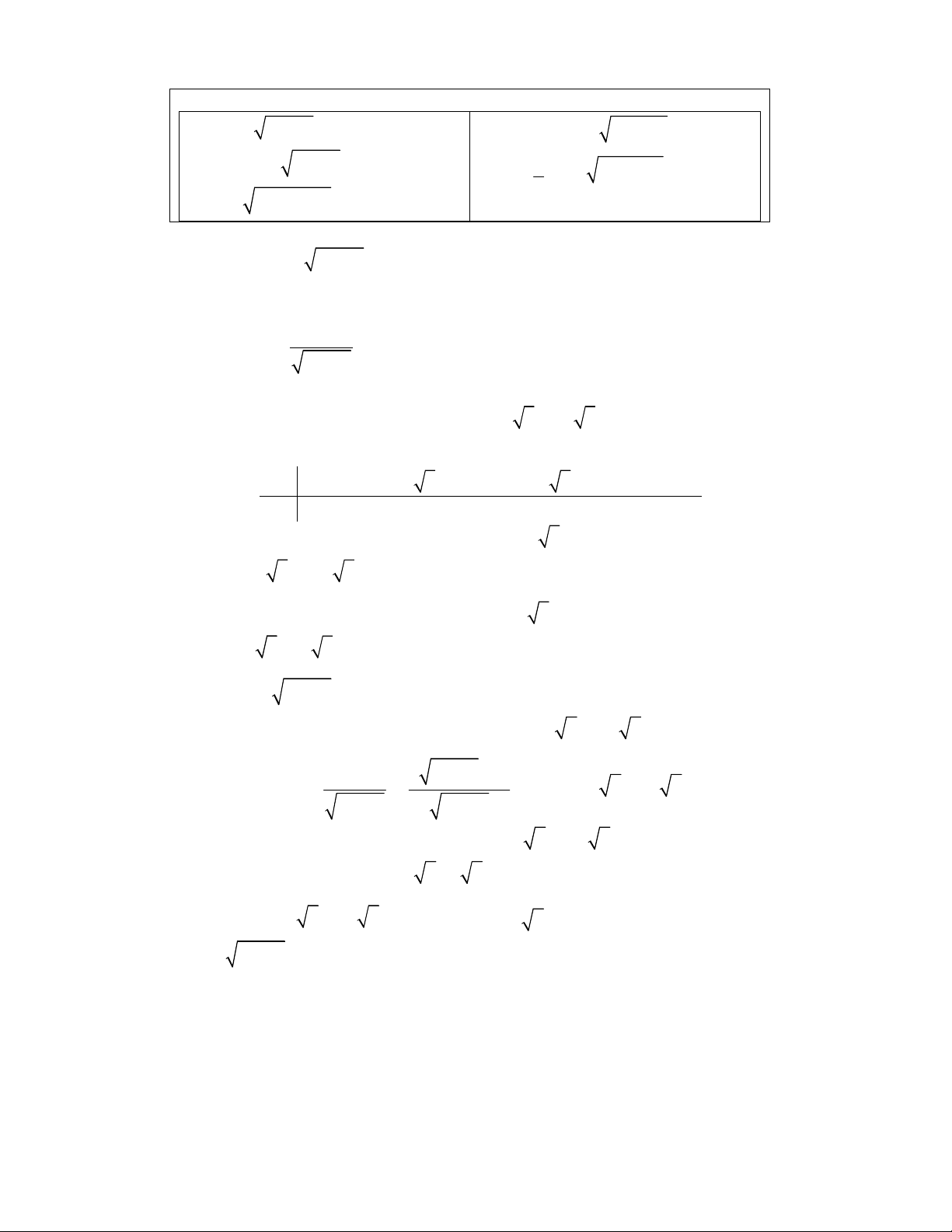
1.
−
=
−
2.
+ −
=
+ +
Nguyn Phú Khánh – à Lt
52
Ví d 2 : Tìm cc tr ca các hàm s :

= −

= − −

= − +

= + − −
 
= − −
Gii :
(
)

= = −
Hàm s ã cho xác nh và liên tc trên on
−
Ta có
( )
−
= ∈ −
−
Hàm s không có o hàm ti các im
.
Suy ra, trên khong
(
)
−
:

= ⇔ = − =
Bng xét du
−
−
−
+
−
i du t âm sang dương khi
qua im
−
thì hàm s t cc tiu ti
im

= −
(
)
− = −
;
i du t dương sang âm khi
qua im
thì hàm s t cc i ti
im

=
(
)
=
.

= − −
Hàm s ã cho xác nh và liên tc trên
(
−∞ − ∪
)

+∞
.
Ta có:
()()

− −
= − = ∈ −∞ − ∪ +∞
− −
.
Hàm s không có o hàm ti các im

.
Suy ra, trên m$i khong
(
)
(
)
−∞ − +∞
:
=
(
)
(
)

∈ −∞ − ∪ +∞ ≤ <
⇔ ⇔ ⇔ =
− =
− =
.
Tương t trên suy ra hàm s t cc tiu ti im
= =
, hàm s
không có cc i.