ươ ệ ố ứ ạ
ệ ố ứ ạ
ệ
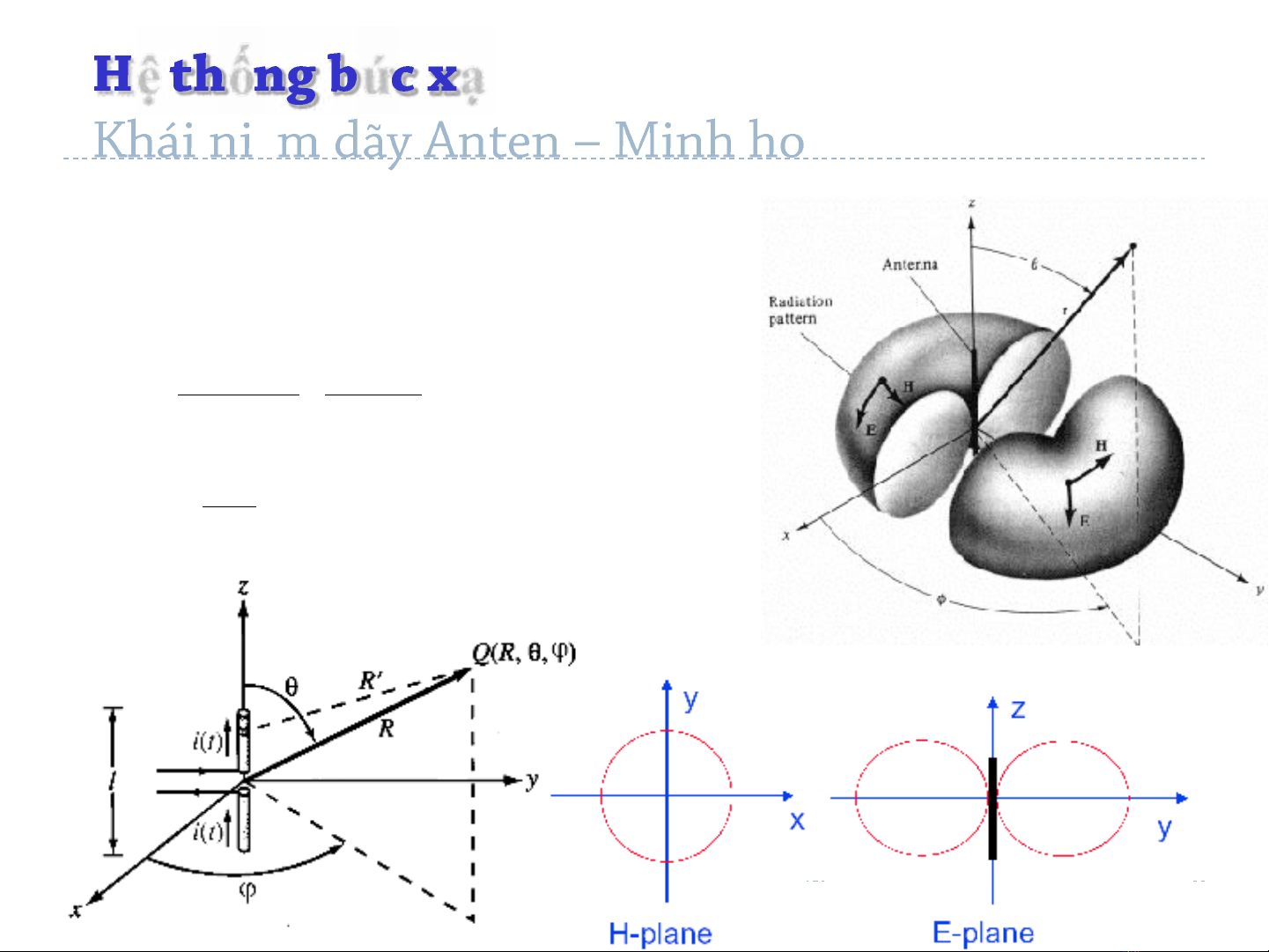
Trong thực tế chúng ta cần độ định hướng cao nhằm thực
hiện liên lạc ở khoảng cách lớn. Có hai cách thực hiện
chính
Tăng kích thước điện của Anten
Phối hợp nhiều Anten với nhau (Antenna Array)
Phương pháp phối hợp nhiều Anten với nhau theo một cấu
trúc vật lý nào đó gọi là Array Anten (tạm dịch dãy Anten
hay dàn Anten)
ệ ố ứ ạ
ệ ạ
Anten Dipole Hertz
m/Vsin
R
ekjI
EjkR
m
4
m/A
E
H
ệ ố ứ ạ
ệ
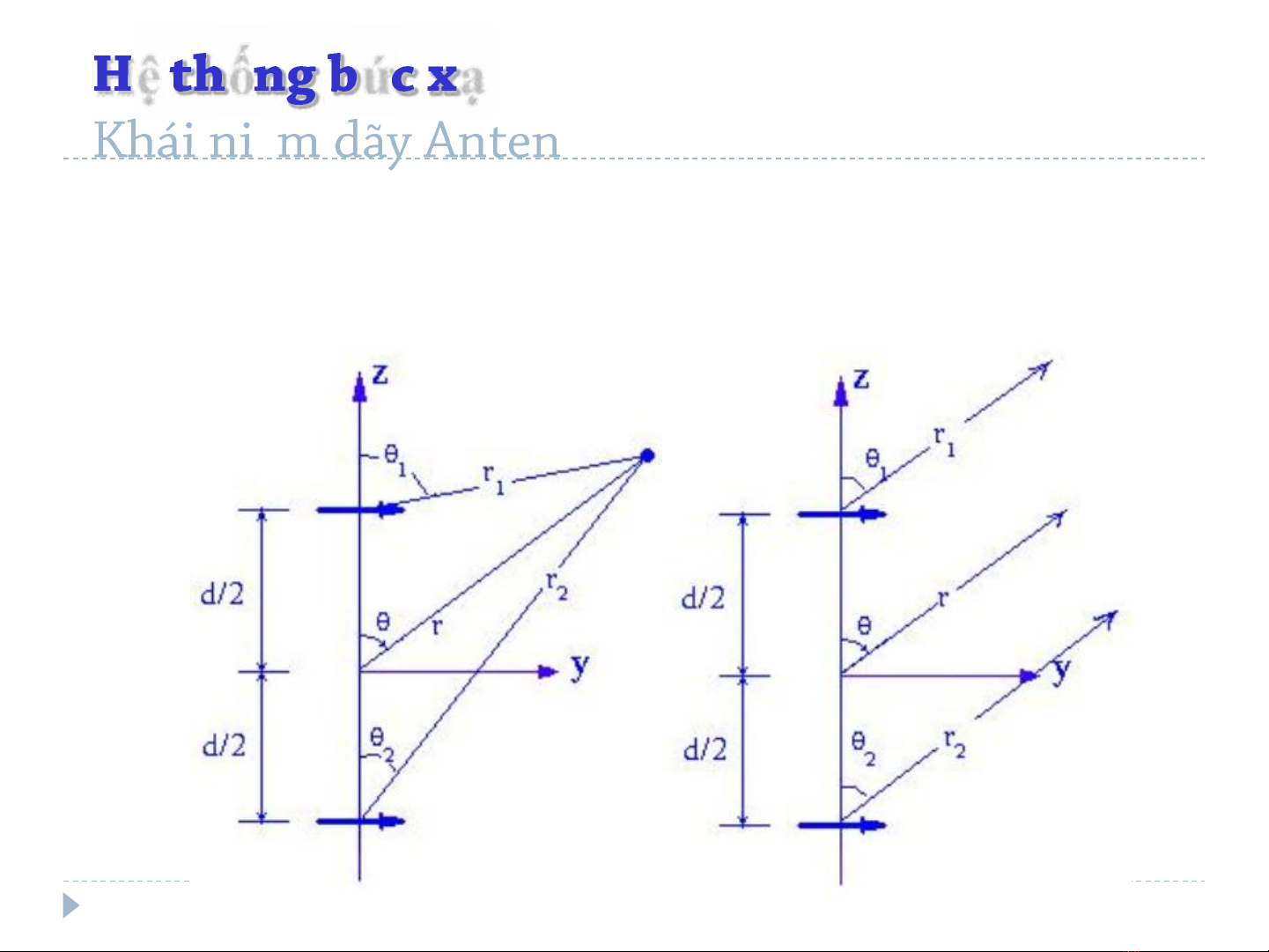
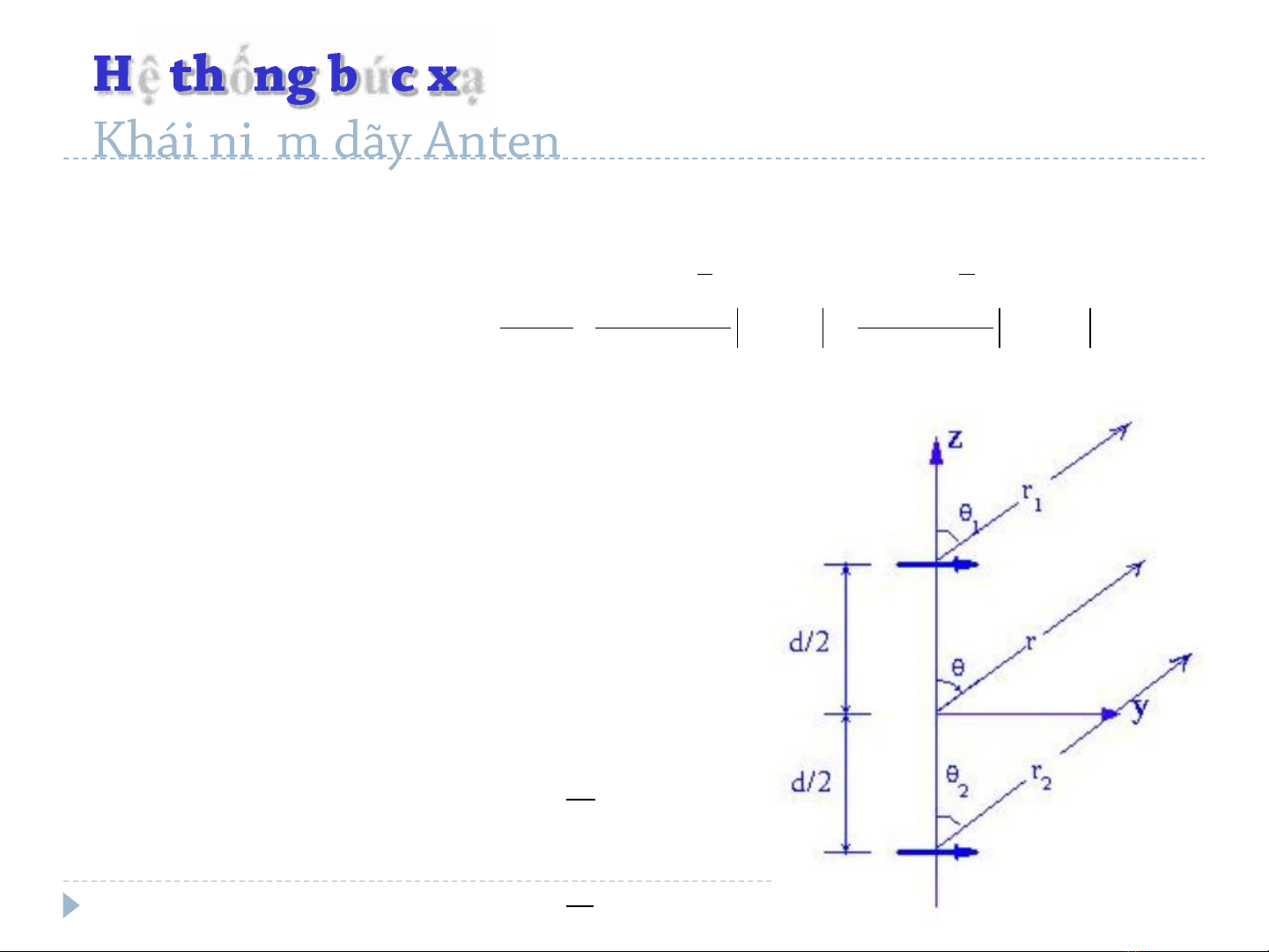
Array 2 phần tử dipole chiều dài hữu hạn đặt ngang theo trục Oz (trong
mặt phẳng z0y)
ệ ố ứ ạ
ệ
2
2
2
1
1
2
21 4cos
r
e
cos
r
e
kI
jiEEE
krjkrj
m
Với:
-β là sự khác pha giữa các elements
-Giả sử biên độ là giống nhau
-Giả sử điểm khảo sát là vùng xa
Khi xeùt pha:
21
;cos
d
rr 2
1
;cos
d
rr 2
2