
ChuyênđềGiảiTíchlớp12 LêNgọcSơn_THPTPhanChuTrinh
1
CHƯƠNG1.
CHUYÊNĐỀ1.SỰĐỒNGBIẾN,NGHỊCHBIẾNCỦAHÀMSỐ
I.KIẾNTHỨCCƠBẢN
1.Địnhnghĩa:Kíhiệu
K
làmộtkhoảng,nửakhoảnghoặcmộtđoạn.
a) Hàm số
f(x)
đglhàmsốđồngbiếntrên
K
, nếu với mọi cặp
12
x,x KÎ
mà
12
xx<
thì
12
f(x ) f(x )<
.
b) Hàm số
f(x)
đglhàmsốnghịchbiếntrên
K
, nếu với mọi cặp
12
x,x KÎ
mà
12
xx<
thì
12
f(x ) f(x )>
.
Hàmsố
f(x)
đồngbiến(nghịchbiến)trên
K
còngọilàhàmtăng(giảm)trên
K
.Hàmsốđồng
biếnhoặcnghịchbiếntrên
K
còngọichunglàhàmsốđơnđiệutrên
K
.
2.Địnhlí
Chohàmsố
yf(x)=
xácđịnhvàcóđạohàmtrên
K
.
a) Nếu
f '(x) 0, x K, f '(x) 0³"Î =
chỉtạimộtsốhữuhạnđiểmthì
f(x)
đồngbiếntrên
K.
b) Nếu
f '(x) 0, x K, f '(x) 0£"Î =
chỉtạimộtsốhữuhạnđiểmthì
f(x)
nghịchbiếntrên
K.
Nếu
f(x)
đồngbiếntrên
K
thì
f'(x) 0, x K³"Î
;nếu
f(x)
nghịchbiếntrên
K
thì
f'(x) 0, x K£"Î
3.Địnhlívềdấutamthứcbậchai
Chotamthức
()
2
f(x) ax bx c a 0=++ ¹
,có
2
b4acD= -
.Tacó:
Nếu
0D<
thì
f(x)
cùngdấuvới
a
,
x"Î
.
Nếu
0D=
thì
f(x)
cùngdấuvới
a
, b
x2a
"¹- .
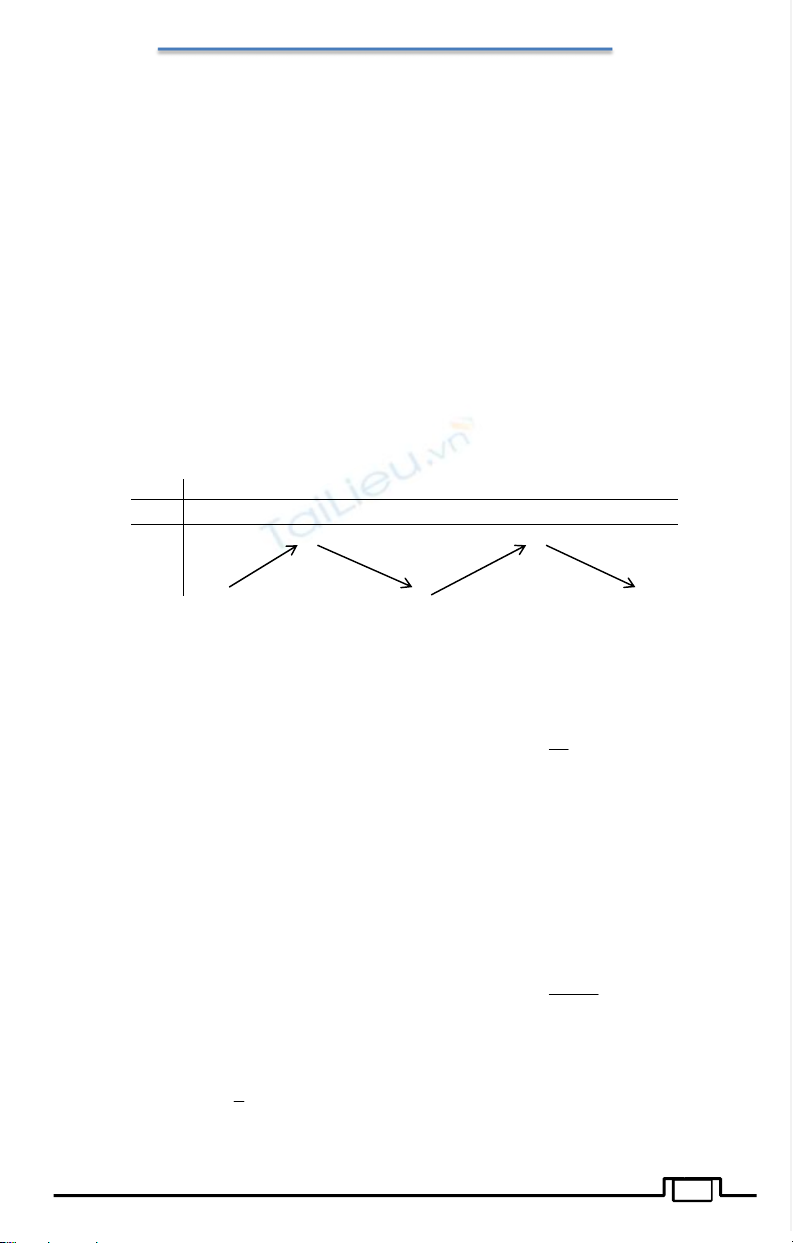
Nếu
0D>
thì
f(x) 0=
cóhainghiệmphânbiệt
( <x )
12 1 2
x;x x
.Tacó:
x
-¥
1
x
2
x
+¥
f(x)
Cùng dấu với
a
0 Trái dấu với
a
0 Cùng dấu với
Hệquả:Chotamthứcbậchai
2
f(x) ax bx c (a 0)=++ ¹
.Tacó:
ChuyênđềGiảiTíchlớp12 LêNgọcSơn_THPTPhanChuTrinh
2
a0
f(x) 0, x 0
ì
ï>
ï
³"
í
ïD£
ï
î
a0
f(x) 0, x 0
ì
ï<
ï
£"
í
ïD£
ï
î
II.PHÂNLOẠICÁCDẠNGBÀITẬP
Dạng1:Tìmcáckhoảngđồngbiến,nghịchbiếncủamộthàmsốchotrước
Bàitập1.Tìmcáckhoảngđồngbiếnnghịchbiếncủahàmsố 42
yx2x3=- + +
Hướngdẫn:
+Tậpxácđịnh
D=
+Tacó 3
y' 4x 4x y' 0 x 0,x 1=- + = = =
.Tacóbảngbiếnthiên:
x
-¥
1
-
0
1
+¥
y'
+
0
-
0
+
0
-
y
4
4
-¥
3
-¥
Vậyhàmsốđồngbiếntrongcáckhoảng
()
;1-¥ -
và
()
0;1
;nghịchbiếntrongcáckhoảng
()
2; +¥
và
()
;1-¥ -
.
Bàitập2.Tìmcáckhoảngđồngbiếnnghịchbiếncủahàmsố
3
2
x
yx3x7
3
=--+
Hướngdẫn:
+Tậpxácđịnh
D
=
+Tacó 2
y' x 2x 3 y' 0 x 1;x 3=--==- =
.Dựavàobảngbiếnthiêntacó:
Hàmsốđồngbiếntrêncáckhoảng
()
;1-¥ -
và
()
3; +¥
;nghịchbiếntrênkhoảng
()
1; 3-
.
Bàitập3.Tìmcáckhoảngđồngbiếnnghịchbiếncủahàmsố
3x 2
y2x 1
-
=+
Hướngdẫn:
+Tậpxácđịnh
D
1
\2
ìü
ïï
ïï
=-
íý
ïï
ïï
îþ

ChuyênđềGiảiTíchlớp12 LêNgọcSơn_THPTPhanChuTrinh
3
+ Ta có
()
2
71
y' 0, x 2
2x 1
=>"¹-
+
. Do đó hàm số đồng biến trên các khoảng
1
;2
æö
÷
ç÷
-¥ -
ç÷
ç÷
ç
èø
và
1;
2
æö
÷
ç÷
-+¥
ç÷
ç÷
ç
èø
Bàitập4.Tìmcáckhoảngđồngbiếnnghịchbiếncủahàmsố
2
x2x6
yx1
++
=-
Hướngdẫn:
+Tậpxácđịnh
D
{}
\1=
+Tacó
()
2
2
x2
x2x8
y' y' 0 x4
x1
é=-
-- ê
==
ê=
ê
-ë
.Dựavàobảngbiếnthiêntacó:Hàmsốđồngbiến
trêncáckhoảng
()
;2-¥ -
và
()
4; +¥
;nghịchbiếntrêncáckhoảng
()
2;1-
và
()
1; 4
.
Bàitập5.Tìmcáckhoảngđồngbiếnnghịchbiếncủahàmsố
2
yxx2=--
Hướngdẫn:
+Tậpxácđịnh
D
()
;1 2;
ùé
=-¥- È +¥
úê
ûë
+Tacó
2
2x 1 1
y' y' 0 x 2
2x x 2
-
===
--
.Dựavàobảngxétdấutacó:Hàmsốđồngbiếntrên
khoảng
()
2; +¥
vànghịchbiếntrênkhoảng
()
;1-¥ -
Bàitập6.Xétsựđồngbiếnnghịchbiếncủahàmsố
yx2sinx,x ;
33
pp
éù
êú
=- Î-
êú
ëû
Hướngdẫn:
+Tậpxácđịnh
D
=
+Tacó y' 1 2cosx y' 0 x 3
p
=- = = (Do
x;
33
pp
éù
êú
Î-
êú
ëû
)
+Dựavàobảngbiếnthiêntacóhàmsốnghịchbiếntrongđoạn
;
33
pp
éù
êú
-
êú
ëû
Bàitậpápdụng
Bàitập1.Xétchiềubiếnthiêncáchàmsốsau:

ChuyênđềGiảiTíchlớp12 LêNgọcSơn_THPTPhanChuTrinh
4
a)
2
y2x4x5=- + +
b)
2
x5
yx
44
=+-
c) 2
yx 4x3=-+
d)
32
yx 2x x2=- +-
e)
2
y (4 x)(x 1)=- -
f)
32
yx 3x 4x1=- +-
g)
42
1
yx2x1
4
=-- h) 42
yx2x3=- - +
i)
42
11
yx x2
10 10
=+-
k)
2x 1
yx5
-
=+
l) x1
y2x
-
=- m) 1
y1
1x
=--
n)
2
2x x 26
yx2
++
=+
o) 1
yx3
1x
=- + - -p)
2
4x 15x 9
y3x
-+
=
Bàitập2.Xétchiềubiếnthiêncáchàmsốsau:
a) 432
y6x8x3x1=- + - -
b)
2
2
x1
yx4
-
=-
c)
2
2
xx1
yxx1
-+
=++
d)
2
2x 1
yx
-
=
e)
2
x
yx3x2
=-+
f)
yx322x=++ -
g)
y2x13x=---
h)
2
yx2x=-
i)
2
y2xx=-
k)
ysin2x x
22
pp
æö
÷
ç÷
=-<<
ç÷
ç
èø
l)
ysin2xx x
22
pp
æö
÷
ç÷
=--<<
ç÷
ç
èø
Dạng2:Sựbiếnthiêncủahàmsốtrênmộtkhoảng
Trongdạngnàytacầnquantâm2chúýsau:
Bấtphươngtrình
u(x) m³
đúng
xI
xI minu(x)m
Î
"Î ³
Bấtphươngtrình
u(x) m£
đúng
xI
xI maxu(x)m
Î
"Î £
Bàitập1.Chohàmsố
() ( )
32
1
ym1xmx3m2x2
3
=-++--.Vớigiátrịnàothìhàmsốluôn
nghịchbiến.
Hướngdẫn:
+Tậpxácđịnh
D=
+Tacó
()
2
y' m 1 x 2mx 3m 1=- + +-
.Đểhàmsốluônnghịchbiếntrên
thì
y' 0, x£"Î
Nếu
m1 0 m 1-= =
.Khiđótacó 1
y' 2x 1 y' 0 x 2
=+££-.Vậy
m1=
khôngthỏa
mãn
ChuyênđềGiảiTíchlớp12 LêNgọcSơn_THPTPhanChuTrinh
5
KhiđóYCBT
2
m1
m1
m10 1
1m
m
'0 2m 5m 2 0 2
2
m2
ì
ï<
ï
ï
ì
ìï
ïï
<
-< é
ï
ïï
ïê
£
íí í
£
ïï ïê
D£ -+-£
ïï ï
îï
îê
ï³
ïê
ïë
î
Bàitập2.Chohàmsố
()( )
32
11
yx m3x2m3x1
32
=-+++-.Vớigiátrịnàothìhàmsốđồng
biếntrênkhoảng
()
4; +¥
Hướngdẫn:
+Tậpxácđịnh
D=
+Tacó
()
2
y' x m 3 x 2m 3=- + + +
.Đểhàmsốđồngbiếntrên
()
4; +¥
thì
y' 0, x 4³">
()
2
2
xm3x2m30,x4
x3x3
m, x 4
x2
- + + +³">
-+
>">
-
Xéthàmsố
)
2
x3x3
f(x) ,x 4;
x2
-+ é
=Î+¥
ê
ë
-
.Tacó
()
2
2
x4x3
f'(x) f'(x) 0 x 1;x 3
x2
-+
====
-
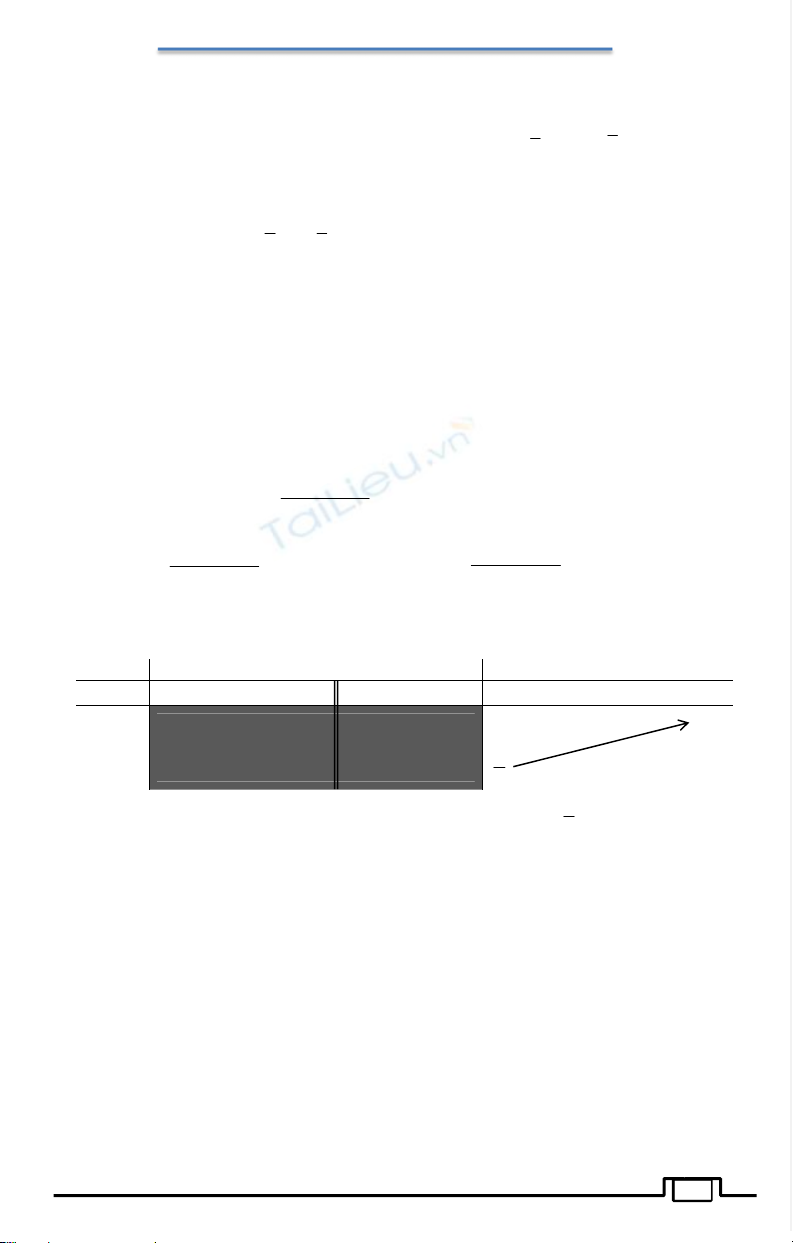
Tacóbảngbiếnthiên:
x
-¥
1
2
3
4
+¥
f'(x)
+
0
-
-
0
+
+
f(x)
+¥
7
2
Từbảngbiếnthiêntathấy:
x4
7
f(x) m, x 4 minf(x) m m 2
³
³"> ³£
Bàitập3.Chohàmsố 32
y x 3x 4mx 2=- - + -
.
a) Vớigiátrịnàocủa
m
thìhàmsốnghịchbiếntrênkhoảng
(
;0ù
-¥ ú
û
b) Tìm
m
đểhàmsốđồngbiếntrênkhoảng
()
2; 1--
Hướngdẫn:
+Tậpxácđịnh
D=
+Tacó
2
y ' 3x 6x 4m=- - +
a) Đểhàmsốnghịchbiếntrênkhoảng
(
;0ù
-¥ ú
û
thì
2
y'0, 0 3x 6x4m,x0£"£ + ³ "£


























