Chuyeân ñeà 13: TÍCH PHAÂN VAØ ÖÙNG DUÏNG
TOÙM TAÉT GIAÙO KHOA
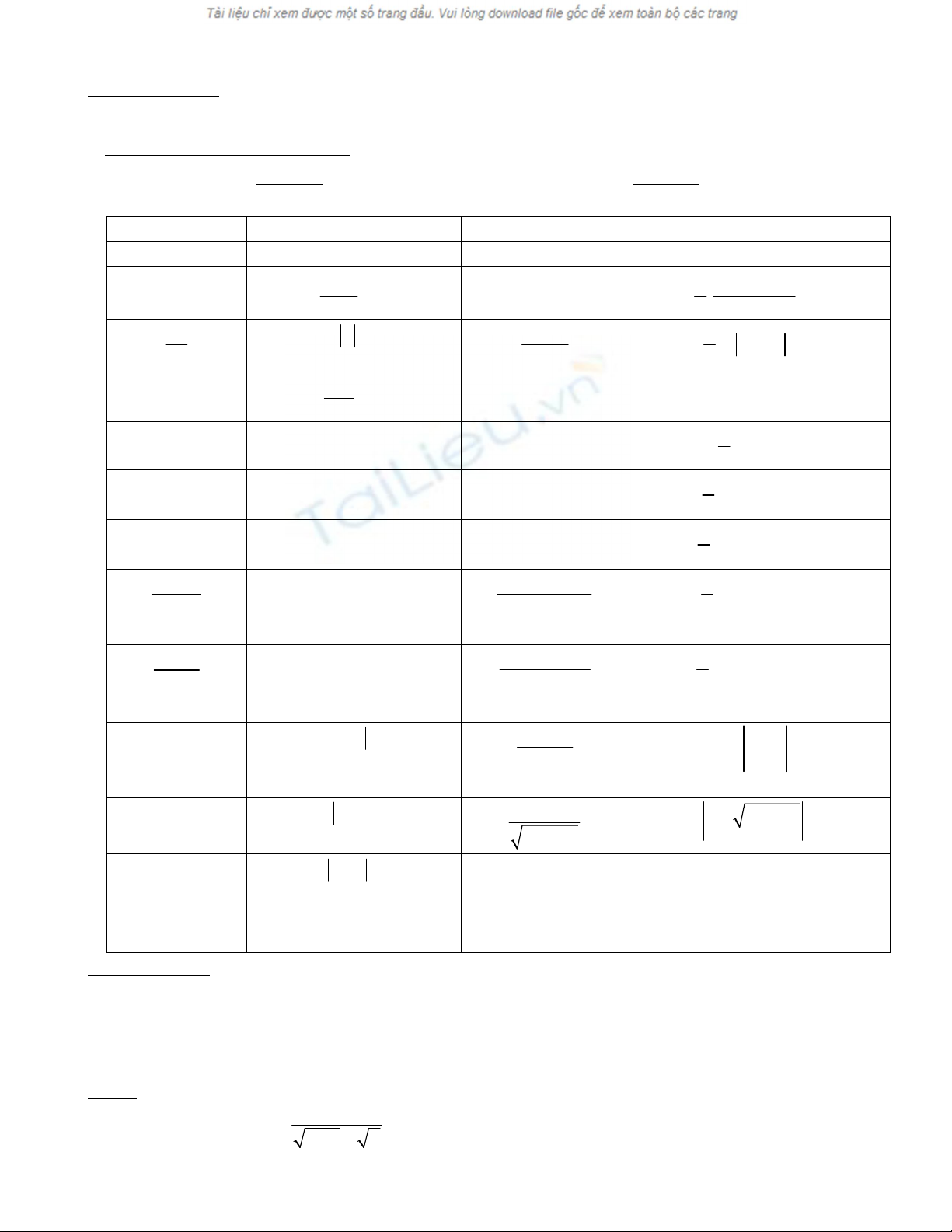
I. Baûng tính nguyeân haøm cô baûn:
Baûng 1 Baûng 2
Haøm soá f(x) Hoï nguyeân haøm F(x)+C Haøm soá f(x) Hoï nguyeân haøm F(x)+C
a ( haèng soá) ax + C
x
α
1
1
xC
α
α
+
+
+ ()ax b
α
+
a
11
()
1
ax b C
α
α
+
+
+
+
1
x
ln
x
C+ 1
ax b
+
1ln ax b C
a++
x
a
ln
x
aC
a+
x
e x
eC+ ax b
e
+
1ax b
eC
a
+
+
sinx -cosx + C sin(ax+b)
1cos( )ax b C
a
−+
+
cosx Sinx + C cos(ax+b)
1sin( )ax b C
a++
2
1
cos
x
tgx + C 2
1
cos ( )ax b
+
1()tg ax b C
a++
2
1
sin
x
-cotgx + C 2
1
sin ( )ax b
+
1cot ( )gax b C
a
−+
+
'()
()
ux
ux ln ( )ux C+ 22
1
x
a
−
1ln
2
x
aC
axa
−
+
+
tgx
ln cos
x
C−+
22
1
x
a+ 22
ln
x
xa C+++
cotgx ln sin
x
C+
Phöông phaùp 1:
• Phaân tích tích phaân ñaõ cho thaønh nhöõng tích phaân ñôn giaûn coù coâng thöùc trong baûng nguyeân
haøm cô baûn
• Caùch phaân tích : Duøng bieán ñoåi ñaïi soá nhö muõ, luõy thöøa, caùc haèng ñaúng thöùc ... vaø bieán ñoåi
löôïng giaùc baèng caùc coâng thöùc löôïng giaùc cô baûn.
Ví duï : Tìm hoï nguyeân haøm cuûa caùc haøm soá sau:
1. 31
() cos 1
fx x
x
x
=+
+− 2. 2
2x 5
f(x) x4x3
−
=
−
+
83

Phöông phaùp 2: Söû duïng caùch vieát vi phaân hoùa trong tích phaân
Ví duï: Tính caùc tích phaân: 1. 5
cos sin
x
xdx
∫ 2. cos
tgx dx
x
∫ 3. 1ln
x
dx
x
+
∫
I. TÍNH TÍCH PHAÂN BAÈNG CAÙCH SÖÛ DUÏNG ÑN VAØ CAÙC TÍNH CHAÁT TÍCH PHAÂN
1. Ñònh nghóa: Cho haøm soá y=f(x) lieân tuïc treân
[
]
;ab . Giaû söû F(x) laø moät nguyeân haøm cuûa haøm soá f(x)
thì:
[]
() () () ()
bb
a
a
f
xdx Fx Fb Fa==−
∫ ( Coâng thöùc NewTon - Leiptnitz)
2. Caùc tính chaát cuûa tích phaân:
• Tính chaát 1: Neáu haøm soá y=f(x) xaùc ñònh taïi a thì : () 0
b
a
fxdx
=
∫
• Tính chaát 2: () ()
ba
ab
f
xdx f xdx=−
∫∫
• Tính chaát 3: Neáu f(x) = c khoâng ñoåi treân
[
]
;ab thì: ()
b
a
cdx c b a
=
−
∫
• Tính chaát 4: Neáu f(x) lieân tuïc treân
[
]
;ab vaø () 0
f
x≥ thì
() 0
b
a
fxdx≥
∫
• Tính chaát 5: Neáu hai haøm soá f(x) vaø g(x) lieân tuïc treân
[
]
;ab vaø
[
]
() () x a;bfx gx≥∀∈ thì
() ()
bb
aa
f
xdx gxdx≥
∫∫
• Tính chaát 6: Neáu f(x) lieân tuïc treân
[
]
;ab vaø ( ) ( m,M laø hai haèng soá)mfx M
≤
≤ thì
() () ()
b
a
mb a f xdx Mb a
−
≤≤
∫−
• Tính chaát 7: Neáu hai haøm soá f(x) vaø g(x) lieân tuïc treân
[
]
;ab thì
[]
() () () ()
bb
aa
b
a
f
x gx dx f xdx gxdx±= ±
∫∫∫
• Tính chaát 8: Neáu haøm soá f(x) lieân tuïc treân
[
]
;ab vaø k laø moät haèng soá thì
.() . ()
bb
aa
kf xdx k f xdx=
∫∫
• Tính chaát 9: Neáu haøm soá f(x) lieân tuïc treân
[
]
;ab vaø c laø moät haèng soá thì
() () ()
bcb
aac
f
xdx f xdx f xdx=+
∫∫∫
• Tính chaát 10: Tích phaân cuûa haøm soá treân
[
]
;ab cho tröôùc khoâng phuï thuoäc vaøo bieán soá , nghóa
laø :
( ) ( ) ( ) ...
bbb
aaa
f x dx f t dt f u du==
∫∫∫
=
84

Baøi 1: Tính caùc tích phaân sau:
85
1) 1
3
0
xdx
(2x 1)+
∫ 2) 1
0
xdx
2x 1+
∫ 3) 1
0
x1 xdx−
∫ 4) 1
2
0
4x 11 dx
x5x6
+
++
∫
5) 1
2
0
2x 5 dx
x4x4
−
−+
∫ 6) 33
2
0
xdx
x2x1++
∫ 7) 666
0
(sin x cos x)dx
π
+
∫ 8) 3
2
0
4sin xdx
1cosx
π
+
∫
9) 4
2
0
1sin2x
dx
cos x
π
+
∫ 10) 24
0
cos 2xdx
π
∫ 11) 2
6
1sin2xcos2x
dx
sinx cosx
π
π
++
+
∫ 12) 1
x
0
1dx
e1+
∫.
13) dxxx )sin(cos
4
0
44
∫−
π
14) ∫+
4
02sin21
2cos
π
dx
x
x 15) ∫+
2
013cos2
3sin
π
dx
x
x 16) ∫−
2
0sin25
cos
π
dx
x
x
17) ∫−+
−
0
2232
4dx
x
x
18) ∫
+
+
−
1
1252
x
x
dx
Baøi 2:
1) 32
3
x1dx
−
−
∫ 2) 42
1
x3x2dx
−
−+
∫ 3) 5
3
(x 2 x 2)dx
−
+−−
∫ 4) 22
2
1
2
1
x2
x
+−
∫dx
5) 3x
0
24dx−
∫ 6)
0
1 cos2xdx
π
+
∫ 7) 2
0
1sinxdx
π
+
∫ 8) dxxx
∫−
2
0
2
Baøi 3:
1) Tìm caùc haèng soá A,B ñeå haøm soá f(x) Asin x B
=
π+ thoûa maõn ñoàng thôøi caùc ñieàu kieän
vaø
'
f(1) 2=
2
0
f(x)dx 4
=
∫
2) Tìm caùc giaù trò cuûa haèng soá a ñeå coù ñaúng thöùc : 223
0
[a (4 4a)x 4x ]dx 12
+
−+ =
∫
II. TÍNH TÍCH PHAÂN BAÈNG PHÖÔNG PHAÙP ÑOÅI BIEÁN SOÁ :
1) DAÏNG 1:Tính I = baèng caùch ñaët t = u(x)
b'
a
f[u(x)].u (x)dx
∫
Coâng thöùc ñoåi bieán soá daïng 1:
[]
∫
=
∫)(
)( )()('.)( bu
au
b
adttfdxxuxuf
Caùch thöïc hieän:
Böôùc 1: Ñaët t dxxudtxu )()( '
=⇒=
Böôùc 2: Ñoåi caän : )(
)(
aut
but
ax
bx
=
=
⇒
=
=
Böôùc 3: Chuyeån tích phaân ñaõ cho sang tích phaân theo bieán t ta ñöôïc
[]
∫
=bfI (tieáp tuïc tính tích phaân môùi)
∫
=)(
)( )()('.)( bu
aua dttfdxxuxu

Tính caùc tích phaân sau:
1) 232
0
cos xsin xdx
π
∫ 2) 25
0
cos xdx
π
∫ 3) 4
2
0
sin 4x dx
1cosx
π
+
∫ 4) 132
0
x1xdx−
∫
5) 223
0
sin2x(1 sin x) dx
π
+
∫ 6) 4
4
0
1dx
cos x
π
∫ 7) e
1
1lnx
dx
x
+
∫ 8) 4
0
1dx
cosx
π
∫
9) e2
1
1lnx
dx
x
+
∫ 10) 11)
1536
0
x(1 x)dx−
∫6
2
0
cosx dx
6 5sinx sin x
π
−+
∫ 12) 34
0
tg x dx
cos2x
∫
13) 4
0
cos sin
3sin2
x
xdx
x
π
+
+
∫ 14) ∫+
2
022 sin4cos
2sin
π
dx
xx
x 15) ∫−+ −
5ln
3ln 32 xx ee
dx 16) ∫+
2
02
)sin2(
2sin
π
dx
x
x
17) ∫
3
42sin
)ln(
π
π
dx
x
tgx 18) ∫−
4
0
8)1(
π
dxxtg 19) ∫+
−
2
42sin1
cossin
π
π
dx
x
xx 20) ∫+
+
2
0cos31
sin2sin
π
dx
x
xx
21) ∫+
2
0cos1
cos2sin
π
dx
x
xx 22) ∫+
2
0
sin cos)cos(
π
xdxxe x 23) ∫−+
2
111 dx
x
x 24) ∫+
edx
x
xx
1
lnln31
25) ∫+
−
4
0
2
2sin1
sin21
π
dx
x
x
2) DAÏNG 2: Tính I = baèng caùch ñaët x =
b
a
f(x)dx
∫(t)
ϕ
Coâng thöùc ñoåi bieán soá daïng 2:
[]
∫
=
∫
=
β
α
ϕϕ
dtttfdxxfI b
a)(')()(
Caùch thöïc hieän:
Böôùc 1: Ñaët dttdxtx )()( '
ϕϕ
=⇒=
Böôùc 2: Ñoåi caän :
α
β
=
=
⇒
=
=
t
t
ax
bx
Böôùc 3: Chuyeån tích phaân ñaõ cho sang tích phaân theo bieán t ta ñöôïc
(tieáp tuïc tính tích phaân môùi)
[]
∫
=
∫
=
β
α
ϕϕ
dtttfdxxfI b
a)(')()(
Tính caùc tích phaân sau:
1) 12
0
1xdx−
∫ 2) 1
2
0
1dx
1x
+
∫ 3) 1
2
0
1dx
4x
−
∫ 4) 1
2
0
1dx
xx1
−+
∫
5) 1
42
0
xdx
xx1
++
∫ 6) 2
0
1
1cos sindx
x
x
π
++
∫ 7)
2
2
2
2
0
xdx
1x−
∫ 8) 222
1
x4xdx−
∫
86

9)
2
3
2
2
1dx
xx 1
−
∫ 10) 32
2
1
93x
dx
x
+
∫ 11) 1
5
0
1
(1 )
xdx
x
−
+
∫ 12) 2
2
2
3
1
1dx
xx−
∫
13) 2
0
cos
7cos2
xdx
x
π
+
∫ 14) 14
6
0
1
1
xdx
x
+
+
∫ 15) 2
0
cos
1cos
xdx
x
π
+
∫ 16) ∫
+
+
−
0
1222
x
x
dx
17) ∫++
1
0311 x
dx 18) ∫−
−
2
15
1dx
x
xx
II. TÍNH TÍCH PHAÂN BAÈNG PHÖÔNG PHAÙP VI PHAÂN:
Tính caùc tích phaân sau:
1) 8
2
3
1
1dx
xx
+
∫ 2) 73
32
01
xdx
x+
∫ 3) 352
0
1
x
xdx+
∫ 4) ln2
x
0
1dx
e2
+
∫
5)
7
3
3
0
1
31
xdx
x
+
+
∫ 6) 223
0
1
x
xd+
∫x
7) ∫+
32
524xx
dx
III. TÍNH TÍCH PHAÂN BAÈNG PHÖÔNG PHAÙP TÍCH PHAÂN TÖØNG PHAÀN:
Coâng thöùc tích phaân töøng phaàn:
[]
∫∫
−=
b
a
b
a
b
adxxuxvxvxudxxvxu )(').()().()(').(
Hay:
[]
∫∫
−=
b
a
b
a
b
avduvuudv .
Caùch thöïc hieän:
Böôùc 1: Ñaët )(
)('
)('
)(
xvv
dxxudu
dxxvdv
xuu
=
=
⇒
=
=
Böôùc 2: Thay vaøo coâng thöùc tích phaân töøng töøng phaàn :
[]
∫∫
−=
b
a
b
a
b
avduvuudv .
Böôùc 3: Tính
[
vaø
]
b
a
vu.∫
b
avdu
Tính caùc tích phaân sau:
1) 2
5
1
lnxdx
x
∫ 2) 22
0
xcos xdx
π
∫ 3)
1x
0
esinxdx
∫
4)
2
0
sin xdx
π
∫ 5) 6)
e2
1
xln xdx
∫3
2
0
xsinx
dx
cos x
π
+
∫
87


























