
Chuyên đề khảo sát hàm số ồ Văn Hoàng
1
Chuyên đề : Khảo sát hàm số và ứng dụng
Các bài toán liên quan đến khảo sát hàm số .
1.Dạng 1:Viết phương trình tiếp tuyến tại điểm M(xM ; yM) .
B1 : hệ số góc tiếp tuyến k = f ‘(xM) .
B2 :Phương trình tiếp tuyến : y – yM = k(x – xM ) .
2.Dạng 2:Viết phương trình tiếp tuyến khi biết dạng của tiếp tuyến
với đồ thị.
B1: Tìm dạng của tiếp tuyến y = g(x) .
B2: Điều kiện tiếp xúc :
( ) ( )
'( ) '( )
f x g x
f x g x
Chú ý :
a. (C) : y = f(x), tx (C/) : y = g(x) khi hệ phương trình sau có
nghiệm :
/
/
/ /
CC
CC
y y
y y
. Nghiệm x của hệ là hoành độ tiếp điểm.
b. Tìm tiếp tuyến với (C) : y = f(x)
*Tại M(xo, yo) : y = f'(xo)(x – xo) + yo.
*Qua M (xo, yo): viết phương trình đường thẳng qua M :
(d): y = k(x – xo) + yo. Dùng điều kiện tx tìm k. Số lượng k = số
lượng tiếp tuyến (nếu f bậc 3 hay bậc 2 / bậc 1 thì số nghiệm x
trong hệ phương trình đk tx = số lượng tiếp tuyến).
* // () : y = ax + b : (d) // () (d) : y = ax + m.
* () : y = ax + b (a 0) : (d) () (d) : y =
1
a
x + m.
Tìm m nhờ đk tx.
c. Bài toán số lượng tiếp tuyến : tìm M (C/) : g(x, y) = 0 sao
cho từ M kẻ được đến (C) đúng n tiếp tuyến (n = 0, 1, 2, ...),
M(xo,yo)(C/)g(xo,yo) = 0; (d) qua M: y = k(x –xo) + yo
(d) tx (C) :
/
C d
C
y y
y k
(1).
Thế k vào (1) được phương trình ẩn x, tham số xo hay yo.
Đặt đk để phương trình có n nghiệm x (số nghiệm x = số tiếp
tuyến), tìm được xo hay yo.
3.Dạng 3:Đường cong : y = ax3 + bx2 + cx + d cắt Ox tại ba điểm
phân biệt khi : ax3 + bx2 + cx + d = 0 có ba nghiệm phân biệt
hay yCĐ .yCT < 0 .
4.Dạng 4:. Điểm đặc biệt của (Cm) : y = f(x, m)
a/ Điểm cố định : M(xo, yo) (Cm), m yo = f(xo, m), m
Am + B = 0, m (hay Am2 + Bm + C = 0, m)
0
0
A
B
(hay
0
0
0
A
B
C
). Giải hệ, được M.
b/ Điểm (Cm) không đi qua, m : M(xo, yo) (Cm), m
yo f(xo,m), m
yo = f(xo, m) VN m Am + B = 0 VN m (hay Am2 + Bm +
C = 0 VN m)
0
0
A
B
(hay
00
00
0
AA
B
C
).
Giải hệ , được M. Chú ý :
AC
B
VN B = 0
0B
A BC VN
c/ Điểm có n đường cong của họ (Cm) đi qua : Có n đường
(Cm) qua M(xo, yo) yo = f(xo, m) có n nghiệm m.
Cần nắm vững điều kiện có n nghiệm của các loại phương trình :
bậc 2, bậc 2 có điều kiện x , bậc 3, trùng phương.
d/Tìm điểm M © : y = ax + b +
c
dx e
có tọa độ nguyên
(a, b, c, d, e Z) : giải hệ
,
M M
M
M M
c
y ax b dx e
x y Z
,
M M
M
M
M
c
y ax b dx e
c
x Z
dx e
,
M M
M
M M
c
y ax b dx e
x Z dx e c
öôùc cuûa
5.Dạng 5:TÂM, TRỤC, CẶP ĐIỂM ĐỐI XỨNG :
a. Cmr đồ thị hàm số nhận điểm M(xM ; yM) làm tâm đối xứng
B1: Đặt
M
M
x x X
y y Y
thay vào y = f(x) và đưa về dạng Y = F(X)
B2: Ta chứng minh hàm số Y = F(X) lẻ (tức là F(-X) = - F(X) )
trên tập xác định nên nhận
0
0
M
M
x x
X
Y y y
làm tâm đối xứng
hàm bậc 3 có tâm đx (điểm uốn), hàm phân thức (gđ 2 tc) tại I :
b. CM hàm bậc 4 có trục đx // (Oy) : giải pt y/ = 0; nếu x = a là
nghiệm duy nhất hay là nghiệm chính giữa của 3 nghiệm :
đổi tọa độ x = X + a, y = Y; thế vào hàm số : Y = F(X);
cm F(–X) = F(X); suy ra F là hàm chẵn, đồ thị có trục đối xứng là
trục tung X = 0 x = a
c. Tìm trên (C) : y = f(x) cặp điểm M, N đối xứng qua I .
giải hệ 4 pt 4 ẩn :
2
2
( )
( )
M N I
M N I
M M
N N
x x x
y y y
y f x
y f x
d. Tìm trên (C) : y = f(x) cặp điểm đ/x qua đt (d) : y = ax +
b :
dt (d) là (d') : y = –
1
a
x + m; lập pt hđ điểm chung của (C) và
(d'); giả sử pt có 2 nghiệm xA, xB, tính tọa độ trung điểm I của
AB theo m; A, B đối xứng qua (d) I (d) m?;
thay m vào pthđ điểm chung, giải tìm xA, xB, suy ra yA, yB.
Tìm tọa điểm uốn : B1: y’’ = 0 có nghiệm xo
yo = f(xo)
B2: Tọa độ điểm uốn : U(xo;yo) .
6.Dạng 6:ĐƠN ĐIỆU :
a. Biện luận sự biến thiên của hàm bậc 3 :
i) a> 0 và y’ = 0 vô nghiệm hàm số tăng trên R (luôn tăng)
ii) a< 0 và y’ = 0 vô nghiệm hàm số giảm trên R (luôn giảm)
iii)a > 0 và y’ = 0 có 2 nghiệm phân biệt x1, x2 với x1 < x2
hàm số đạt cực đại tại x1 và đạt cực tiểu tại x2. Ngoài ra ta có :
+ x1 + x2 = 2x0 với x0 là hoành độ điểm uốn.
+ hàm số tăng trên (, x1); + hàm số tăng trên (x2, +);
+ hàm số giảm trên (x1, x2)
iv)a < 0 và y’ = 0 có 2 nghiệm phân biệt x1, x2 với x1 < x2
hàm đạt cực tiểu tại x1 và đạt cực đại tại x2 thỏa điều kiện x1
+ x2 = 2x0 (x0 là hoành độ điểm uốn). Ta cũng có :
+ hàm số giảm trên (, x1); + hàm số giảm trên (x2, +);
+hàm số tăng trên (x1, x2)
b. Biện luận sự biến thiên của y =
2
ax bx c
mx n
i) Nếu a.m > 0 và y/ = 0 vô nghiệm thì hàm tăng ( đồng biến) trên
từng khỏang xác định.
ii) Nếu a.m < 0 và y/ = 0 vô nghiệm thì hàm giảm (nghịch biến)
trên từng khỏang xác định.
Chuyên đề khảo sát hàm số Hồ Văn Hoàng
2
iii) Nếu a.m > 0 và y/ = 0 có 2 nghiệm phân biệt x1, x2thì hàm đạt
cực đại tại x1 và đạt cực tiểu tại x2 thỏa x1< x2 và
1 2
2
x x p
m
.
iv) Nếu a.m < 0 và y/ = 0 có 2 nghiệm phân biệt x1, x2 thì hàm đạt
cực tiểu tại x1 và đạt cực đại tại x2 thỏa x1 < x2 và
1 2
2
x x p
m
.
c.Tìm m để hàm số bậc 3, bậc 2/bậc 1 đồng biến
(nghịch biến) / miền xI: đặt đk để I nằm trong miền đồng
biến (nghịch biến) của các BBT trên; so sánh nghiệm pt y/ = 0
với .
7.Dạng 7:Tìm giá trị lớn nhất của hàm số và giá trị nhỏ nhất của
hàm số .
Trên khoảng (a ; b) thì ta lập bảng xét dấu của y’ và yCĐ là
GTLN; yCT là GTNN .
Trên đoạn [a ; b] thì ta giải phương trình :y’ = 0 có nghiệm x1 ;
x2 ; … thuộc [a ; b]
Tính y(x1) ; y(x2) ; … ; y(a) ; y(b) .Số lớn nhất là GTLN ; số nhỏ
nhất là GTNN.
8.Dạng8: Cực trị f có đúng n cực trị f/ đổi dấu n lần.
f đạt cực đại tại xo
/
//
( ) 0
( ) 0
o
o
f x
f x
;
f đạt cực tiểu tại xo
/
//
( ) 0
( ) 0
o
o
f x
f x
1/ Hàm bậc 3 (hay bậc 2 / bậc 1) có cực trị
phương trình y’ = 0 có 2 nghiệm phân biệt
*Tính yCĐ.yCT :
Hàm bậc 3 : y = y/ (Ax + B) + (Cx+ D);
yCĐ.yCT = (CxCĐ + D).(CxCT + D), dùng Viète với pt y/ = 0.
Hàm bậc 2/ bậc 1 :
u
yv
; yCĐ.yCT =
/ /
/ /
( ). ( )
( ). ( )
CÑ CT
CÑ CT
u x u x
v x v x
,
dùng Viète với pt y/ = 0.
2/ Hàm trùng phương: y = ax4 + bx2 + c có 1 cực trị ab 0,
3 cực trị ab < 0
9.Dạng 9:Viết phương trình đường thẳng đi qua điểm cực đại và
điểm cực tiểu (cực trị)
a) Hàm phân thức : y =
2
ax bx c
dx e
=
( )
( )
f x
g x
.
B1: Điều kiện để có cực trị là y’ = 0 có hai nghiệm phân biệt .
B2: có 2 nghiệm xCĐ ; xCT thì yCĐ =
'( )
'( )
CD
CD
f x
g x
& yCT =
'( )
'( )
CT
CT
f x
g x
B3:Kết luận :Đường thẳng qua cực trị là : y =
'( )
'( )
f x
g x
.
b) Hàm đa thức :y = ax3 + bx2 + cx + d .
B1:Điều kiện để có có cực trị là y’ = 0 có hai nghiệm phân biệt .
B2:Chia đa thức :Lấy y chia y’ .Kết quả có dạng :
y = y’(x) .[
1
3 9
b
xa
] +
2
2(3 ) 9
.
9 9
ac b ad cb
x
a a
.
B3:Giả sử có hai nghiệm xCĐ ; xCT thì
yCĐ =
2
2(3 ) 9
.
9 9
CD
ac b ad cb
x
a a
; yCT =
2
2(3 ) 9
.
9 9
CT
ac b ad cb
x
a a
B4:Kết luận :đường thẳng qua cực trị là:y =
2
2(3 ) 9
.
9 9
ac b ad cb
x
a a
.
10.Dạng 10:Vẽ đồ thị hàm số có chứa dấu giá trị tuyệt đối .
1) Hàm số y = f(|x|) .
Phương pháp :
B1: Vẽ đồ thị hàm số y = f(x) .
B2: Giữ nguyên phần x ≥ 0 , lấy đối xứng phần x > 0 qua Oy
2) Hàm số y = |f(x)| .
Phương pháp :
B1: Vẽ đồ thị hàm số y = f(x) .
B2: Giữ nguyên phần y ≥ 0 , lấy đối xứng phần y <0 qua Ox3)
Hàm số y = |f(|x|)| .
Phương pháp :
B1: Vẽ đồ thị hàm số y = f(x) .
B2: Giữ nguyên phần x ≥ 0 , lấy đối xứng phần x >0 qua Oy
B3: Giữ nguyên phần y ≥ 0 , lấy đối xứng phần y < 0qua Ox
Nhớg(x) = f(–x) : đối xứng qua (Oy);
g(x) = – f(x) : đối xứng qua (Ox).
11. Dạng 11: Bài toán tìm quỹ tích .
B1: Tìm toạ độ quỹ tích M
( )
( )
x f m
y g m
.
B2:Khử tham số m giữa x và y ta có phương trình quỹ tích .
B3:Giới hạn quỹ tích là dựa vào điều kiện của tham số m , suy ra
điều kiện của x và y .
Nếu xo = a thì M (d) : x = a.
Nếu yo = b thì M (d) : y = b.
12.Dạng 12 : Bài toán TƯƠNG GIAO :
*Phương trình hđ điểm chung của (C) : y = f(x) và (C/) : y = g(x)
là : f(x) = g(x). Số nghiệm pt = số điểm chung.
*Tìm m để (Cm) : y = f(x, m) và (C/m) : y = g(x, m) có n giao
điểm : Viết phương trình hoành độ điểm chung; đặt đk để pt có n
nghiệm. Nếu pt hoành độ điểm chung tách được m sang 1 vế :
F(x) = m; đặt điều kiện để (C):y=F(x) & (d): y = m có n điểm chung.
*Biện luận sự tương giao của (Cm) và (C/m) :
Nếu pt hđ điểm chung dạng : F(x) = m : lập BBT của F; số
điểm chung của (Cm) và (C/m) = số điểm chung của (C) và (d).
PThđ điểm chung, không tách được m, dạng ax2 + bx + c = 0
(x ) hay dạng bậc 3 : x = f(x) = 0 : lập , xét dấu , giải
pt f(x) = 0 để biết m nào thì là nghiệm của f, với m đó, số
nghiệm bị bớt đi 1.
Bài toán đồ thị hàm số y = ax4 + bx2 + c cắt trục hoành tại 4
điểm phân biệt có hoành độ lập thành 1 cấp số cộng .
B1:Phương trình hoành độ giao điểm của ( C) với trục hoành là
ax4 + bx2 + c = 0 (1).
Đặt t = x2 (điều kiện :t > 0) .Khi đó phương trình (1) trở thành :
at2 + bt + c = 0 (2).
Điều kiện để (C ) cắt trục hoành tại 4 điểm thì phương trình (1)
có 4 nghiệm phân biệt
phương trình (2) có 2 nghiệm dương
phân biệt
0
0
0
S
P
B2:Giả sử (2) có hai nghiệm là 0 < n < m.thì phương trình (1) có
4 nghiệm là :
; ; ;m n n m
.
Để 4 nghiệm lập thành 1 cấp số cộng thì
2m n n
m = 9n (3) .
B3:Ap dụng định lí viet :
.
n m S
n m P
(4) .
Kết hợp (3) và (4) để tìm m và n .Từ đó suy ra cấp số cộng :
; ; ;m n n m
.
BIỆN LUẬN SỐ NGHIỆM PT BẰNG ĐỒ THỊ :
a. Cho pt : F(x, m) = 0; tách m sang 1 vế : f(x) = m; lập BBT của
f (nếu f đã khảo sát thì dùng đồ thị của f),
số nghiệm = số điểm chung.
b. Với pt mũ, log,
, .
, lượng giác: đổi biến; cần biết mỗi
biến mới t được mấy biến cũ x; cần biết đk của t .
1/ Giải bất phương trình bằng đồ thị :
f < g a < x < b, f > g
x a
b x
f g a x b , f g
x a
x b
2/ Tìm 2 điểm thuộc hai nhánh đồ thị sao cho khoảng cách đó là
ngắn nhất .
B1: Từ y =
( )
( )
f x
g x
đổi hệ trục toạ độ Y =
a
X
(với a là hằng số ).
a
b
f
g
Chuyên đề khảo sát hàm số Hồ Văn Hoàng
3
B2: Lấy A
;a
và B
;a
với
0; 0
.
Ví dụ 1. Cho hàm số y = f(x) = mx3 + 3mx2 (m 1)x 1
a) Khảo sát và vẽ đồ thị hàm số với m = 1.
b) Xác định m để hàm y = f(x) không có cực trị
Giải.a) với m = 1, y = x3 + 3x2 1
b) y’ = 3mx2 + 6mx (m 1). Điều kiện cần vàđủ để y = f(x)
không có cực trịlà phương trình f’ (x) = 0 không có hai nghiệm
phân biệt, nghĩa là
2
01
004
' 9 3 ( 1) 0
m
mm
m m m
Ví dụ 2. Cho hàm số y = x3 + mx2 m
a) Khảo sát và vẽ đồ thị hàm số khi m = 3
b) Khi nào đồ thị cắt trục hoành tại 3 điểm phân biệt
c) Xác định m sao cho x 1 y 1.
Giải a) m = 3 y = x3 + 3x2 3
b) Đồ thị cắt trục hoành tại 3 điểm phân biệt khi và chỉ khi hàm
số có cực đại và cực tiểu và ycđ. yct < 0
y’ = 3x2 + 2mx = x(3x + 2m). y’ = 0 x = 0 và x = 2m/3
Hàm có cực đại và cực tiểu 2m/3 0 m 0
3
c®
4 27
. 0 . 2 / 3 0
27
ct
m m
y y y y m m
2
4 27 0m
3 3
2
m
Vậy đồ thị cắt Ox tại 3điểm phân biệt
3 3 / 2m
c)
1y x
với
1x
0 1y m
.
Với
1m
, m 0, ta có
2 / 3 1m
.
với m [1, 1]\
0
để
1y x
với
1x
điều kiện đủ là
3
4
1 2 / 3 27
m
y m m
(vì y (1) = 1, y(1) = 1, y (0) = mđều thuộc [1, 1]).
Nhưng
3 2
4 4
, 1 1
27 27
m m
m m
khi
1m
.
m = 0 cũng thỏa mãn. Kết luận m [1, 1].
Ví dụ 3. Cho hàm số y = (m 2)x3 mx + 2 (1)
a) Khảo sát và vẽ đồ thị hàm số khi m = 1
b) C minh rằng khi m (0, 2) hàm không có cực đại và cực tiểu.
c) C minh rằng đồ thị của hàm số (1) luôn qua ba điểm cố định.
Giảib) y’ = 3(m 2)x2 m
m (0, 2) m / 3(m 2) < 0 và phương trình y’ = 0 vô nghiệm.
c) y = mx3 2x3 mx + 2 mx (x2 1) 2(x3 1) y = 0
Phương trình đúng với mọi m R
2
3
0 2
1 0 1 4
2 1 1 0
o o
o o
o o
o o o o
x y
x x x y
y x x y
Đồ thị luôn đi qua 3 điểm cố định (0, 2), ( 1, 4), (1, 0).
Ví dụ 4. Cho y = f(x) = 2x3 3(2m + 1)x2 + 6m (m + 1)x + 1(1)
a) Tìm quĩ tích điểm uốn
b) Tìm quĩ tích điểm cực đại
c) Tìm quĩ tích trung điểm đoạn nối điểm CĐ& CT của đồ thị.
Giải.a) y’ = 6x2 6(2m + 1) x + 6m(m + 1)
y” = 12x 6(2m + 1), y” = 0
2 1
2
m
x
y” đổi dấu khi x biến thiên qua (2m + 1)/2.
Vậy điểm uốn là
2 1 2 1
,
2 2
m m
U f
.
Từ
2 1
2
m
x
suy ra
2 1
2
x
m
,
thay vào phương trình y = f(x) ta thu được
33
2 1.
2
y x x
Vậy quĩ tích đồ thị hàm
33
2 1.
2
y x x
b) y’ = 6[x2 (2m + 1)x + m (m + 1)], y’ = 0
1
x m
x m
Đó là hai nghiệm phân biệt và rõ ràng
y’(x)<0 x (m, m + 1); y’(x)>0 x(, m) (m + 1, +)
Vậy hàm luôn có cực đại và cực tiểu tại x = m và x = m + 1.
Điểm cực đại là (m, f(m)). Khử m bằng cách thay m = x, vào (1)
ta được y = 2x3 + 3x2 + 1. Vậy đồ thị của hàm y = 2x3 + 3x2 + 1
là quĩ tích các điểm cực đại của hàm số khi m thay đổi.
c) Trung điểm của đoạn nối điểm cực đại và cực tiểu làđiểm uốn,
mà quĩ tích đã biết ở câu a).
Ví dụ 5. Cho hàm số y = f(x) = x4 mx3 (2m + 1)x2 + mx + 1
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với a = 0.
b) Tìm các điểm trên trục tung sao cho qua đó có thể kẻ được ba
tiếp tuyến với đồ thị của y = f(x) với m = 0.
c) Xác định m sao cho phương trình f(x) = 0 có hai nghiệm khác
nhau lớn hơn 1.
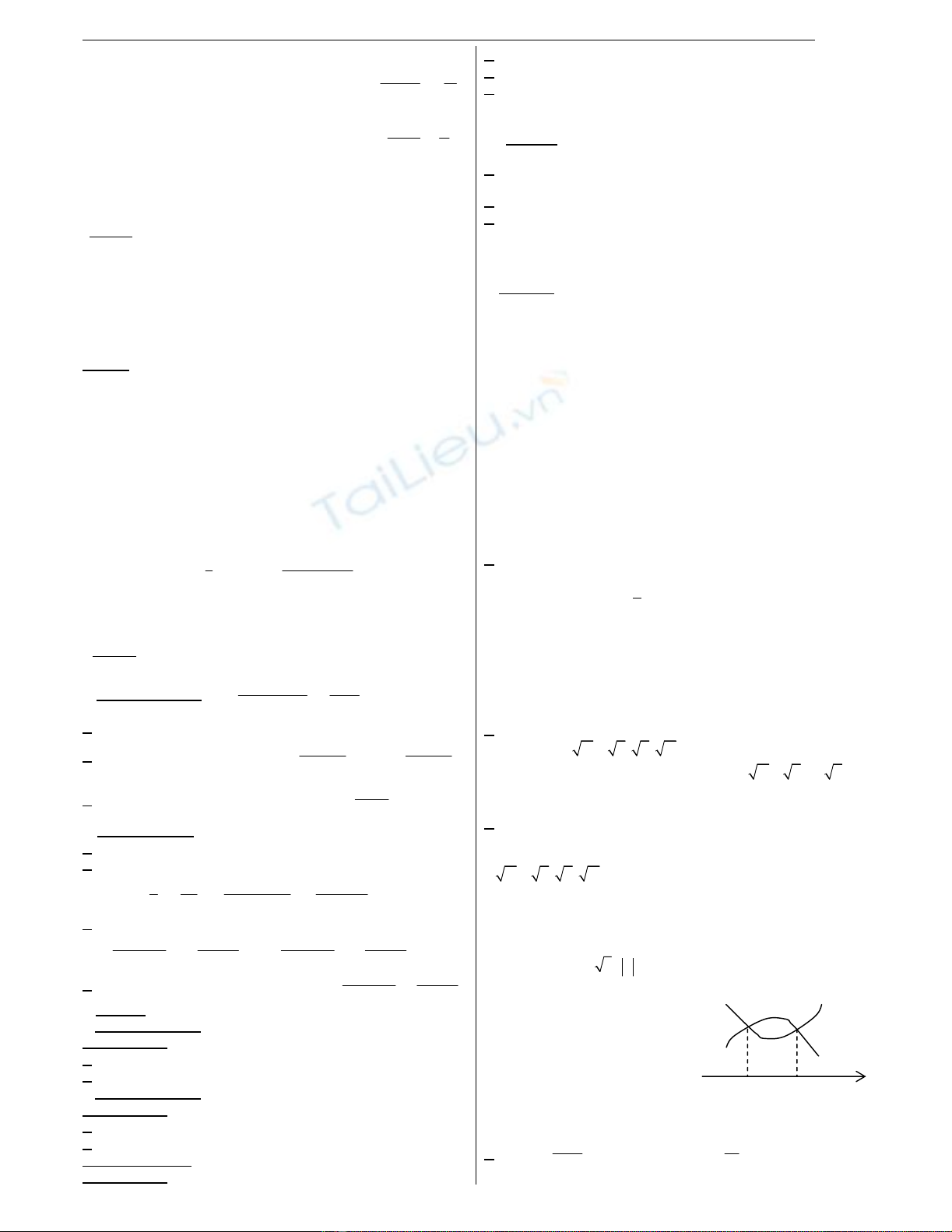
Giải.a) Với m = 0, hàm số có dạng y = x4 x2 + 1
y
1
3/4
-
2
/2 0
2
/2 x
b) f(x) là hàm chẵn nên trục tung là trục đối xứng. Nên qua điểm
trên trục tung kẻ được ba tiếp tuyến với đồ thị thì phải có 1 tiếp
tuyến song song với trục hoành. Từ đó điểm cần tìm phải làđiểm
M(0, 1). Ta kiểm tra điều đó.
Giả sử y = ax + 1 là tiếp tuyến khác qua a. Khi đó phải có
4 2
3
1 1
4 2
o o o
o o
x x ax
x x a
với xo là hoành độ tiếp điểm.
Giải hệ đó (đối với (xo, a)) ta có các nghiệm (0, 0), và
3 / 3, 4 3 / 9 .
Từ đó các tiếp tuyến khác y = 1 là
4 3 / 9 1y x
.Vậy điểm cần tìm là M (0, 1).
c) Phương trình x4mx3 (2m + 1)x2 + mx + 1 = 0 (1)
2
2
1 1 2 1 0x m x m
x
x
(2)
Đặt
1
t x x
. t’(x) =
2
1
1x
> 0, do đó x > 1 thì t(x) > t(1) = 0.
Bây giờ (2) có dạng t2 mt (2 1) = 0. (3)
Vậy để có hai nghiệm lớn hơn 1, phương trình (3) phải có hai
nghiệm dương. Tức là phải có
22
4 1 2 0 8 4 0
/ 2 / 2 0 0
1 2 0 1/ 2
m m m m
S m m
p m m
4 2 5,1/ 2m
Ví dụ 6. Cho hàm số
1mx
yx m
(1)
a) Khảo sát và vẽ đồ thị hàm số với m = 2.
b) Với m nào hàm đồng biến, nghịch biến không đổi?
c) Cm rằng khi m thay đổi đồ thị luôn đi qua hai điểm cố định.
d) Tìm quĩ tích tâm đối xứng của đồ thị.

Chuyên đề khảo sát hàm số Hồ Văn Hoàng
4
Giải.a) Với m = 2,
2 1 3
2
2 2
x
yx x
. Tập xác định R\
2
Đồ thị có hai tiệm cận x = 2 và y = 2.
2
3
'2
yx
0 với x 2.
Vậy y giảm trên các khoảng (, 2) và (2, +).
Bảng biến thiên
Đồ thị có tâm đối xứng là giao điểm I của hai tiệm cận.
b)
2
2
1
'm
yx m
,x m
Nếu 1 m2 > 0 ( 1 < m < 1) thì hàm luôn đồng biến trên
(, m) và (m, +).
Nếu 1 m2 < 0 ( m [1, 1] thì hàm luôn nghịch biến trên
mỗi khoảng xác định
Nếu 1 m2 = 0 ( m = 1) thì y không đổi
m = 1 y 1 trên R\
1
m = 1 y 1 trên R\
1
c) Giả sử (xo, yo) làđiểm cố định. Khi đó
1 0 m
o
o o o o
x m
x y m x y
2
0 1, 1
1 1, 1
1
o o
o o o o
o o o o
o
x y
x y x y
x y x y
x
Vậy đồ thị luôn đi qua hai điểm cố định (1, 1) và (1, 1).
d) Tâm đối xứng là giao của hai tiệm cận tức làđiểm (m, m). Khi
m thay đổi các điểm này vạch đường thẳng y = x.
Vd 7. Cho hàm số
2 2
1
m x m
yx m
a) Khảo sát và vẽ đồ thị hàm số khi m = 1
b) Chứng minh rằng với mọi m tiệm cận xiên của đồ thị luôn
tiếp xúc với một parabôn cố định. Xác định parabôn đó.
c) Tìm tất cả các điểm mà tiệm cận xiên không đi qua
Giải Với m = 1,
2
2 1 1
2 1
1 1
x
y x
x x
a) * D = R\
1
*
2
1
' 2 1
yx
,
y’ = 0
2
12
x
y’ > 0
2 2
,1 1 ,
2 2
x
y’ < 0
2 2
1 ,1
2 2
x
.
Tiệm cận xiên y = 2(x + 1) Tiệm cận đứng x = 1
b) Ta có tiệm cận xiên y = (m + 1)x + m2 + m
Giả sử các tiệm cận xiên trên luôn tiếp xúc parabôn cố định y =
ax2 + bx + c, a 0.
Ta có
2 2
ax + bx c m 1 x m +m (1)
1
2 1 (2)
2
m b
ax b m x a
Từ đó : ax2 + bx + c = (2ax + b)x + (2ax + b) (2ax + b 1)
(4a2+a)x2+(4ab2a)x+b2bc = 0 có nghiệm kép x =
4 2
(4 1)
ab a
a a
vậy:
1
2
m b
a
=
4 2
(4 1)
ab a
a a
(4a+1)m = 12ab8a+b1Đm
2 2 2
4 1 0 1/ 4
12ab 8a b 1 0 1/ 2
1/ 4
4a a x (4ab 2a)x b b c 0
a a
b
c
Như vậy parabôn cần tìm là
2
1 1 1 0
4 2 4
y x x
c) Giả sử (xo, yo) là điểm mà tiệm cận không đi qua.
Từ đó phương trình yo = (m + 1)xo + m2 + m vô nghiệm, hay
phương trình m2 + (xo + 1)m + xo−yo = 0 vô nghiệm
= (xo + 1)2− 4(xo− yo) < 0
2
1 1 1
4 2 4
o o o
y x x
Đó là các điểm nằm trong parabôn
2
1 1 1
4 2 4
y x x
.
ĐH Năm 2006:
1/ A : ( C ) y = 2x3−9x2+ 12x −4 a/ KSHS.
b/Xác định m để pt : 2
32
9 12 0x x x m
có 6 nghiệm pb.
2/ B : ( C)
21
2
x x
yx
a/ KSHS.
b) Viết pttt của ( C ) & vuông góc với tiệm cận xiên .
HD: b/ k=-1 : x0=−2
2 3 2
; 3
2 2
y
3/ D: (C) y = x3−3x +2 a/ KSHS.
b/ Đt (D) qua A(3;20) có hsg m. Định m để (D ) cắt ( C ) tại 3
điểm khác nhau . Đsố : m>15/4 và m ≠ 24.
ĐH Năm 2005 :
1/ A : ( Cm ) y = mx +1/x a/ KSHS.
b/Xác định m để HS có ctrị và khoảng cách từ cực tiểu đến tiệm
cận xiên bằng
1
2
2 2
2
2
1 1
( ;2 ); ( ; ) 2
1 1
2 1 0 1
m m m
CT m d m tcx
mm m
m m m
2/ B : ( C)
2( 1) 1
1
x m x m
yx
. a/ KSHS.
b) CMR: Với mọi m, ( Cm ) luôn có CĐ, CT và khoảng cách
giữa hai điểm đó bằng
20
.
HD: b/ Cđ( -2;m-3) CT(0;m+1). D =
20
3/ D: (Cm):
3 2
1 1
3 2 3
m
y x x
a/ KSHS.
b/ Gọi M (Cm) có xM=–1. Tìm m để tại M có tt // d: 5x −y = 0
ĐH Năm 2004:
1/ A : ( C)
23 3
2( 2)
x x
yx
a/ KSHS.
b/ Tìm m để y = m cắt (C) tại A,B sao cho : AB=1 .
HD: pt hđộ : x2+ (2m 3) x + 3 2m = 0 có
0 3 / 2; 1/ 2m m
2
1 2 1 2 1 2
1 5
1 1 ( ) 4 2
AB x x x x x x m
2/ B: ( C)
3 2
12 3
3
y x x x
a/ KSHS.
b/Viết pttt của ( C ) tại điểm uốn . CMR pttt nầy cóHSG nhỏ nhất
Chú ý : a > 0: HSGóc NN, a < 0 : HSG lớn nhất .
3/ D: (Cm)
3 2
3 9 1y x mx x
a/ KSHS khi m = 1
-2 -1 1 2 3
1
2
3
4
5
6
7
8
x
y

Chuyên đề khảo sát hàm số Hồ Văn Hoàng
5
b/ Tìm m để điểm uốn của (Cm) thuộc đường thẳng y = x +1.
HD: I thuộc đt m=0, m =
2
ĐH BNăm 2003 :(C)
3 2
3y x x m
a/KSHS khi m = 2 .
b/Tìm m để ( Cm ) có hai hai điểm đối xứng qua gốc toạ độ .
HD : YCĐB xo≠0 sao cho y(x0)≠ − y(−x0)
Thếx0vào hai vế để phương trình có 2 ngh:
2
0
3 0.x m m
ĐH Năm 2002:
1/A: (C):
3 2 2 3 2
3 3(1 )y x mx m x m m
a/KSHS khi m =1
b/Tìm k để
3 2 3
3 0x x k
có 3 nghiệm phân biệt.
c/ Viết phương trình đường thẳng qua hai cực trị của ( Cm )
b/ (
3 2
0 3 4 1 3; 0; 2k k k k k
)
c/ (Cm) có cực trị với mọi m .Chia y cho y/ ta có : y = 2x+ m−m2
2/ B:
4 2 2
( 9) 10y mx m x
a/KSHS khi m =1.
b/Tìm m để HS có 3 ctrị .
HD: b/ y’= 2x( 2mx2+ m2−9) = 0
2 2
0
2 9 0(2)
x
mx m
.
(2) Có 2ngh ph biệt khác 0
2
2
03
90 2
2
mm
mm
xm
DỰ BỊ 1 B:Cho ( C )
4 2
6 5y x x
; a/ KSHS.
b/ Tìm m để phương trình x4−6x2−
2
log 0m
có 4 ngh ph biệt
HD:
2 2 9
1
4 log 5 5 9 log 0 1
2
m m m
DỰ BỊ 1A/2004:Cho (C)
4 2 2
2 1y x m x
;
a/KSHS khi m = 1.
b/Tìm m để HS có 3 cực trị tạo thành tam giác vuông cân .
HD: y’= 0 x=0 ;x=
m
. Vậy HS có 3 ctrị khi m ≠ 0
Gọi A(0;1); B; C có hoành độ
m
và có tung độ là : 1−m4.
4 4
( ; ); ( ; )AB m m AC m m
.
Vì y là hàm số chẵn nên AC = AB . YCĐB
2 8 6
. 0; 0 0 1 1AB AC m m m m m
DỰ BỊ 1 B –2004 Cho
3 2 2
2 2y x mx m x
a/KSHS khi m = 1 .
b/Tìm m để HS đạt cực tiểu tại x=1 .
HD: y đạt ctiểu tại x = 1
,
,,
(1) 0 1.
(1) 0
ym
y
DỰ BỊ B1 –2003: ( C)
2
( 1)( )y x x mx m
a/KS-HS ( C )khi m=4 .
b/Tìm m để (Cm) cắt Ox tại 3 điểm phân biệt .
HD:
20x mx m
có 2 ngh ≠1m < 0 V m > 4 và m ≠ ½
DỰ BỊ B2 –2003: ( C)
2 1
1
x
yx
a/KSHS.
b/Gọi I là giao điểm của hai tiệm cận. Tìm M
(C): tiếp tuyến
của ( C ) tại M vuông góc IM .
HD : Ta có ktt .kIM =−1. Mà ktt = −1/(xM−1)2kIM = (xM−1)2
Mặt khác I(1;2) kIM =
1 1
1
21
M M
M
M
x x
y
x
=1
Vậy : (xM−1)2 = 1
0 1
2 3
M M
M M
x y
x y
Vậy : M(0;1) M(2;3) .
DỰ BỊ D2 –2003: (C)
3 2
2 3 1y x x
a/ KSHS .
b/ ( d ) qua M(0;1) có HSG là k, tìm k: (d) cắt (C) tại 3 điểm phân
biệt. (k > 9/8 và k
0)
DỰ BỊ 1 –2002:
4 2 1y x m x m
;
a/KSHS khi m =8.
b/Tìm m để (Cm) cắt Ox tại 4 điểm phân biệt
HD: pt t2−mx + m −1 = 0 Có hai nghiệm dương
2
( 2) 0 1
02
1 0
mm
S m m
P m
DỰ BỊ 3 –2002:(C)
3 2
1 1
2 2
3 3
y x mx x m
a/ Cho m = ½ . Khảo sát sự biến thiên của đồ thị của hàm số ,
b/ Viết phương trình tiếp tuyến của đồ thị hàm số biết rằng tiếp
tuyến đó song song với đường thẳng D: y = 4x + 2
c/ Tìm m thuộc khoảng (0;5/6) sao cho hình phẳng giới hạn bởi
đồ thị hàm số (1) và các đường thẳng x=0, x=2, y=0 có diện tích
bằng 4. Hd: b/ 2 tt : ( d1) y=4x-26/3 ; ( d2) y=4x+73/6
DỰ BỊ 6 –2002:Cho ( C )
3 2
12 3
3
y x x x
a/ KSHS
b/Tính diện tích hình phẳng: ( C ) và Ox . ĐS : S= 9/4 ( Đvdt )
Tự luyện
Bài 1: Cho hàm số
3
( ) 3 (1)y x m x
1/Khảo sát sự biến thiên của đồ thị của hàm số khi m=1
2/Tìm m để hàm số đã cho đạt cực tiểu tại điểm có hoành độ x=0
3/Tìm k để hệ sau có nghiêm
3
2 3
2 2
1 3 0
1 1
log log ( 1) 1
2 3
x x k
x x
Bài 2: Cho hàm số
1(1)
1
x
yx
1) Khảo sát sự biến thiên của đồ thị của hàm
2) Tìm m để đường thẳng D:y = 2x + m cắt (C ) tại 2 điểm phân
biệt A,B sao cho tiếp tuyến của (C ) tại A, B song song nhau
3) Tìm tất cả các điểm M thuộc (C ) sao cho khoảng cách từ M
đến giao điểm 2 đường tiệm cận là ngắn nhất
Bài 3: Cho hàm số
2(1)
1
x
yx
.Cho điểm A(0;a). Xác định a
để từ A kẻ được 2 tiếp tuyến tới (C) sao cho 2 tiếp điểm tương
ứng nằm về 2 phía đối với trục Ox
HD a ≠−1 & a > − 2 có 2 nghiệm phân biệt. y1.y2< 0
ĐS a> − 2/3 và a ≠1
Bài 4: Cho hàm số
4 2 2
2 1 (1)y x m x
1/ Khảo sát sự biến thiên của đồ thị của hàm số khi m=1
2/Tìm m để đồ thị của hàm số (1) có 3 điểm cực trị là 3 đỉnh của
một tam giác vuông cân
Bài 5: Cho hàm số
4 2
4 (1)y x x m
.Giả sử đồ thị cắt trục
hoành tại 4 điểm phân biệt .Hãy xác định m sao cho hình phẳng
giới hạn bởi đồ thị (C) và trục hoành có diện tích phần phía trên
và phần phía dưới đối với trục hoành bằng nhau
HD: ĐK cắt 0<m<4 vẽ minh hoạ gọi x1, x2, x3, x4, là nghiệm
Strên= Sduói
34
3
0
( ) ( )
xx
x
f x dx f x dx
.
Vận dụng tính chất đối xứng , định ly Viét m = 20/9.
Bài 6 : Cho hàm số
3 2
3 2y x x
.
1) Khảo sát và vẽ (C) .
2) Cmr tiếp tuyến của đồ thị tại điểm uốn có hệ số góc nhỏ nhất
3) Tìm các điểm trên (C) vẽ đúng một tiếp tuyến đến (C) .
4) Viết phương trình tiếp tuyến của (C) .
a) Tại diểm M(-1 ;-2)
b) Qua diểm A( -1;-2)
c) Tiếp tuyến song song với đường thẳng y = 9x+1 .
5) Tìm các điểm trên đường thẳng :y= -2 có thể vẽ đến (C)
a) 3 tiếp tuyến . b) 2 tiếp tuyến vuông góc .
6) Biện luận theo m số nghiệm của pt :


























